Secant 方法求方程多个根

Secant 方法介绍

Secant Method

函数 Secant_Methods 简介

1.函数定义

[c, errColumn] = Secant_Method(f, a, b, N, convergence_type, tolerance)

2.输入

%   f - function handle
%   a - start position of interval bracket
%   b - end position of interval bracket
%   N [optional]  - max iteration number
%   convergence_type [optional]  -  [= 1] absolute error tolerances
%                                   [= 0] relative error tolerances
%   tolerance [optional] - [convergence_type = 1] absolute error tolerances
%                          [convergence_type = 0] relative error tolerances
% 

3.输出

%   c - approximation of root r ( f(r) = 0 )
%   errColumn - the absolute/relative errors during the progress
%   convergence_step -  the number of steps taken, if the method doesn't
%                       convergence, [convergence_step = inf]

注意，errColumn 长度为 N，若在第k步收敛解后，剩余元素都与收敛步误差相同

4.代码

function [c, errColumn, convergence_step] = Secant_Method(f, a, b, N, convergence_type, tolerance)
% Use Secant Method to find roots of equation [f(x) = 0]
% 
% Input:
%   f - function handle
%   a - start position of interval bracket
%   b - end position of interval bracket
%   N [optional]  - max iteration number (default value: 10)
%   convergence_type [optional]  -  [= 1] absolute error tolerances (default)
%                                   [= 0] relative error tolerances
%   tolerance [optional] - [convergence_type = 1] absolute error tolerances
%                          [convergence_type = 0] relative error tolerances
% 
% Output:
%   c - approximation of root r ( f(r) = 0 )
%   errColumn - the absolute/relative errors during the progress
%   convergence_step -  the number of steps taken, if the method doesn't
%                       convergence, [convergence_step = inf]
% Usages:
% 
%   1. use default value
%       f = @(x) x^2 - 1
%       c = false_position(f, 0, 2)
% 
%   2. user set value
%       c = false_position(f, 0, 2, 20, 0, 1e-5)
% 
% Warnning:
%   1. if f(a) and f(b) have the same sign, the function returns an Nan.
%   2. if the false position lines outside the bracket interval, the
%   function will throws an error.
%   3. After N times iteration, if the method does not converge, an message
%   will be printed on the command window and return the current vaule.

%% check input parameters

% check the interval is really a bracket
if (a > b)
    error('please check the bracket!');
end

% check that that neither end-point is a root
% if f(a) and f(b) have the same sign, throw an Nan.
if( f(a) == 0 )
    c = a;
    return;
elseif ( f(b) == 0 )
    c = b;
    return;
elseif ( f(a) * f(b) > 0 )
    c = Nan;
    return;
end

% check max iteration number exits
% default value is 10
if ~exist('N', 'var')
    N = 10;
end% if

% check choice of error tolerances
% default value is 1
if ~exist('convergence_type', 'var')
    convergence_type = 1;
    tolerance = 1e-6;
end% if

% check the tolerances is positive
if tolerance <= 0
    error('the tolerances should be positive!');
end

% relative error tolerances
errColumn = zeros(N, 1);

%% iteration
% iterate at most N times

c_old = a;
convergence_step = inf;

for k = 1:N
    %% find the false position
%     c = (a*f(b) + b*f(a))/(f(b) - f(a));
    c = ( b*f(a) - a*f(b) )/(f(a) - f(b));
    
    % check c lies within the bracketing interval
    if (c < a) || (c > b)
        error('convergence problem occurs! please reset bracket interval.')
    end
    
    %% reset bracketing interval
    % Check if c is a root
    if ( f(c) == 0 )
        % return c
        return;
    elseif ( f(c)*f(a) < 0 ) 
        % if f(a) and f(c) have opposite signs
        % set [a, c] as the new bracketing interval      
        b = c;
    else
        % if f(b) and f(c) have opposite signs
        % set [c, b] as the new bracketing interval    
        a = c;
    end

    %% cal the absolute/relative errors
    switch convergence_type
        case 0 % relative error
            errColumn(k) = abs( (c - c_old)/c_old );
            if errColumn(k) < tolerance
                convergence_step = k;
                errColumn(k:end) = errColumn(k);
                % set convergence step 
                % set the remaining step errors
                return;
            end
        case 1 % absolute error
            errColumn(k) = abs( f(c) );
            if errColumn(k) < tolerance
                % set convergence step 
                % set the remaining step errors
                convergence_step = k;
                errColumn(k:end) = errColumn(k);
                return;
            end
    end% switch

c_old = c;
end

fprintf( 'the method did not converge

' );
end

算例 Q1.m

find all roots of (1000000x^3 − 111000x^2 + 1110x = 1)

• 绘制函数函数图像，寻找方程根所在区间
  

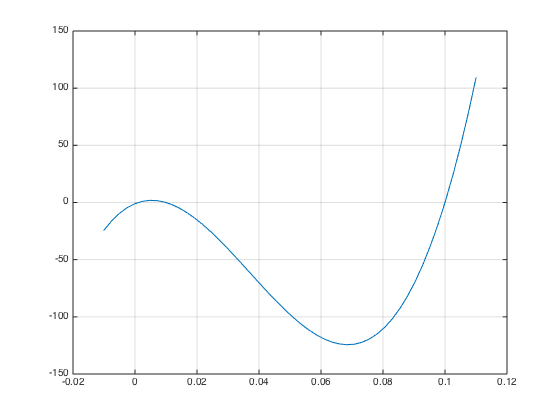
• 选取区间
  选取3个区间分别为 ([-0.01, 0.005], [0.005, 0.06], [0.06, 0.11])。

• 计算
  第一个区间 ([-0.01, 0.005]) 为例，选择绝对误差为 (10^{-6})，迭代40次。得到误差随迭代次数变化关系为
  
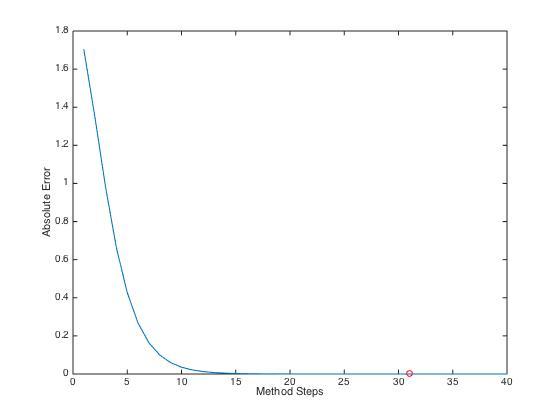
  其中红色点代表第31步方法收敛位置。

• 结果
  最终得到方程三个根为

r =

    0.0010
    0.0100
    0.1000

• 脚本

%% Q1
f = @(x) 1000000*x.^3 - 111000*x.^2 + 1110*x - 1;

% plot function
x = linspace(-0.01, 0.11, 50);
y = f(x);
figure; plot(x,y); grid on;

% set interval bracket
a(1) = -0.01; a(2) = 0.005; a(3) = 0.06; a(4) = 0.11;

% cal roots in a loop
r = zeros(3,1);

for ib = 1:3
    [r(ib), errColumn, con_step] = Secant_Method(f, a(ib), a(ib+1), 40);
    
    if ib == 1
        figure; plot(errColumn); hold on;
        plot(con_step, errColumn(con_step), 'ro');
        xlabel('Method Steps'); ylabel('Absolute Error')
    end% if
end% for