二叉查找树
二叉查找树是二叉树中最常用的一种类型,也叫二叉搜索树。
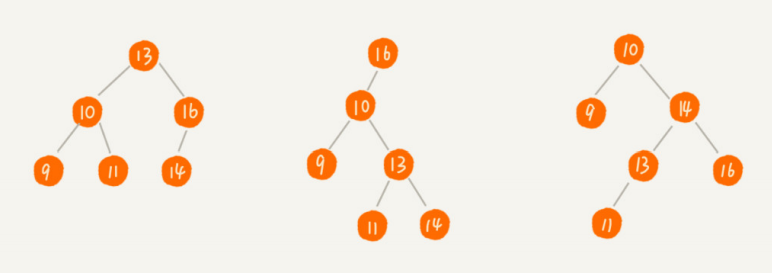
二叉查找树要求,在树中的任意一个节点,其左子的每个节点的值,都要小于这个节点的值,而右子树节点的值都大于这个节点的值。
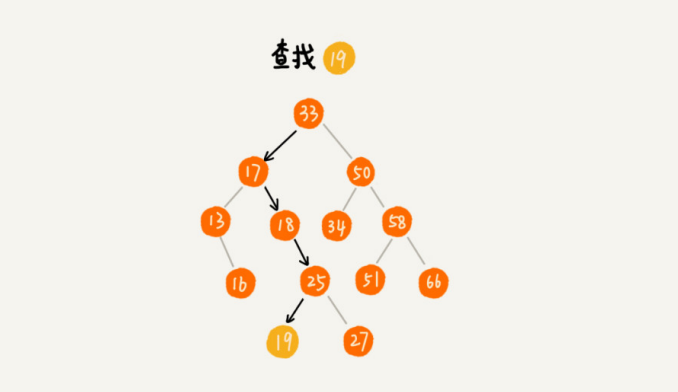
二叉查找树的查找操作
- 对比当前节点(首个是根节点),相等则返回。
- 大于则从右子树查找
- 小于则从左子树查找
- 直到叶子节点,如果不存在,则返回空,存在则返回。
代码实现:
public class BinarySearchTree
{
private Node tree;
public Node Find(int data)
{
Node p = tree;
while (p != null)
{
if (data < p.data) p = p.left;
else if (data > p.data) p = p.right;
else return p;
}
return null;
}
public class Node
{
public int data;
public Node left;
public Node right;
public Node(int data)
{
this.data = data;
}
}
}
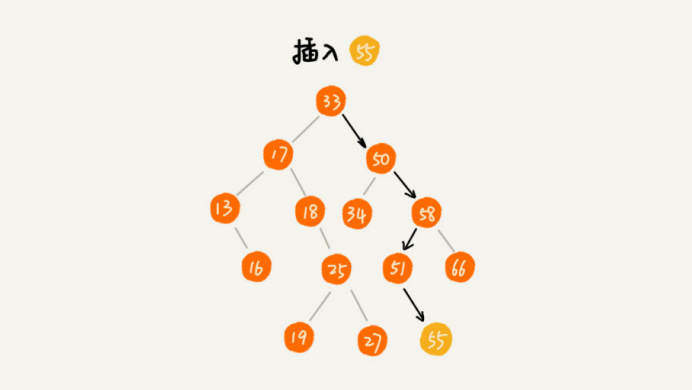
二叉查找树的插入操作
插入操作有点类似查找操作。
- 如果要插入的数据比当前节点的数据大,并且节点的右子树为空,则新数据直接插入右子节点的位置
- 如果不为空,再递归遍历右子树,查找插入位置
- 同理,插入的数据比当前节点的数据要小,并且节点的左子树为空,则插入左子节点的位置。
- 如果不为空,再递归遍历左子树,查找插入位置。
代码实现:
public void Insert(int data)
{
if (tree == null)
{
tree = new Node(data);
return;
}
Insert(tree, data);
}
private void Insert(Node node, int data)
{
if (data > node.data)
{
if (node.right == null)
node.right = new Node(data);
else
Insert(node.right, data);
}
else if (data < node.data)
{
if (node.left == null)
node.left = new Node(data);
else
Insert(node.left, data);
}
}
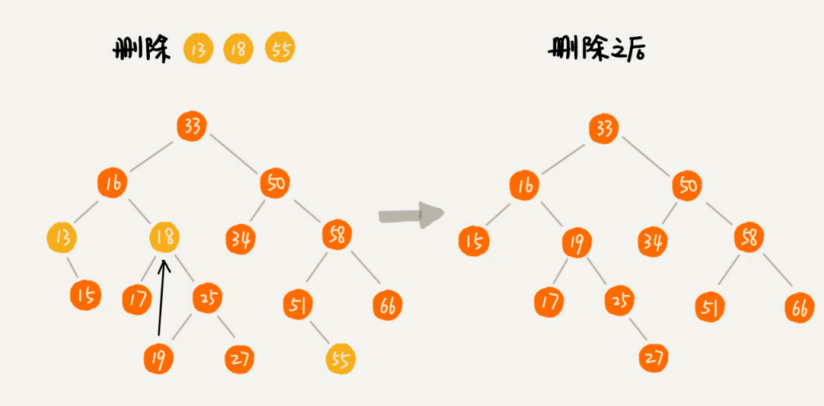
二叉查找树的删除操作
相比二叉查找树的查找和插入操作,删除操作要复杂不少,有三种情况:
- 情况一:删除节点没有没有子节点,父节点的左节点(或右节点)设置为null。
- 情况二:删除节点只有一个子节点,父节点的左节点(或右节点)直接连接此叶子节点。
- 情况三:删除节点有两个子节点,则查找删除节点的右子树的最小节点,替换到删除节点的位置,然后再删除掉这个最小节点。
代码实现:
public void Delete(int data)
{
Node p = tree;
Node pp = null;
while (p != null)
{
if (data < p.data)
{
pp = p;
p = p.left;
}
else if (data > p.data)
{
pp = p;
p = p.right;
}
else
{
break;
}
}
if (p == null) return;
// 删除的结点有两个结点
if (p.left != null && p.right != null)
{
// 查找右子树中最小节点
Node minP = p.right;
Node minPP = p; // minPP表示minP的父节点
while (minP.left != null)
{
minPP = minP;
minP = minP.left;
}
p.data = minP.data; // 将minP的数据替换到p中
p = minP; // 下面就变成了删除minP了
pp = minPP;
}
// 删除的是结点是叶子结点或仅有一个结点
Node child;
if (p.left != null) child = p.left;
else if (p.right != null) child = p.right;
else child = null;
if (pp == null) tree = null; // 如果pp=null,表示树只有一个结点
else if (pp.left == p) pp.left = child;
else pp.right = child;
}
二叉查找树的其他操作
除了插入、删除、查找操作之外,二叉查找树还可以支持快速查找最大节点和最早小节点、前驱节点和后继节点。
另外还有一个重要的特性,就是中序遍历二叉查找树,可以输出有序的数据序列,时间复杂度是O(n)。因此,二叉查找树也叫作二叉排序树。
二叉查找树的时间复杂度分析

最坏情况,二叉查找树退化成链表,时间复杂度为O(n)。
最好情况,二叉查找树是完全二叉树(或满二叉树),时间复杂度为O(height)。而完全二叉树的高度是log2(n),即时间复杂度是O(logn)。
课后思考
今天我讲了二叉树高度的理论分析方法,给出了粗略的数量级。如何通过编程,求出一棵给 定二叉树的确切高度呢?
使用广度遍历,通过两个队列,一个记录广度遍历的顺序,一个记录广度遍历的节点的高度。遍历过程中,找到最大的高度。
代码实现:
public int GetHeight()
{
if (tree == null) return 0;
// 广度遍历,通过两个队列,queueN记录广度遍历的顺序,queueH记录queueN相对应节点的高度
Queue<Node> queueN = new Queue<Node>();
Queue<int> queueH = new Queue<int>();
queueN.Enqueue(tree);
queueH.Enqueue(1);
int maxHeight = 1;
while (queueN.Count > 0)
{
Node p = queueN.Dequeue();
int height = queueH.Dequeue();
if (maxHeight < height) maxHeight = height;
if (p.left != null) { queueN.Enqueue(p.left); queueH.Enqueue(height + 1); }
if (p.right != null) { queueN.Enqueue(p.right); queueH.Enqueue(height + 1); }
}
return maxHeight;
}