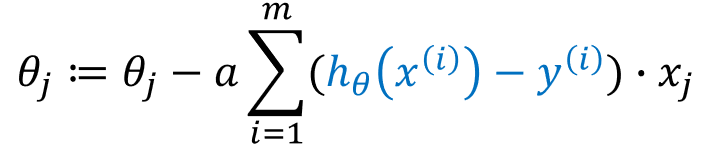1. LR的直观表述
1.1 直观表述
今天我们来深入了解一个工业界应用最多,虽然思想简单但也遮挡不住它NB光芒的绽放的一个分类预测模型,它就是LR模型。LR模型可以被认为就是一个被Sigmoid函数(logistic方程)所归一化后的线性回归模型!为啥这么说呢?我们来看一下它的假设函数的样子:
![]()
首先来解释一下![]() 的表示的是啥?它表示的就是将因变量预测成1(阳性)的概率,具体来说它所要表达的是在给定x条件下事件y发生的条件概率,而
的表示的是啥?它表示的就是将因变量预测成1(阳性)的概率,具体来说它所要表达的是在给定x条件下事件y发生的条件概率,而![]() 是该条件概率的参数。看到这个公式可能一脸懵逼,那我们将它分解一下:
是该条件概率的参数。看到这个公式可能一脸懵逼,那我们将它分解一下:

很容易看出将(1)代入到(2)中是不是就得到了LR模型的假设函数啦。(1)式就是我们介绍的线性回归的假设函数,那(2)式就是我们的Sigmoid函数啦。什么?为什么会用Sigmoid函数?因为它引入了非线性映射,将线性回归![]() 值域映射到0-1之间,有助于直观的做出预测类型的判断:大于等于0.5表示阳性,小于0.5表示阴性。
值域映射到0-1之间,有助于直观的做出预测类型的判断:大于等于0.5表示阳性,小于0.5表示阴性。
其实,从本质来说:在分类情况下,经过学习后的LR分类器其实就是一组权值![]() ,当有测试样本输入时,这组权值与测试数据按照加权得到
,当有测试样本输入时,这组权值与测试数据按照加权得到
![]()
这里的![]() 就是每个测试样本的n个特征值。之后在按照Sigmoid函数的形式求出
就是每个测试样本的n个特征值。之后在按照Sigmoid函数的形式求出![]() ,从而去判断每个测试样本所属的类别。
,从而去判断每个测试样本所属的类别。
由此看见,LR模型学习最关键的问题就是研究如何求解这组权值!
1.2 决策边界
经过上面的讲解,我们应该对LR要做什么,有个一个大体上的把握。接下来,我们在深入一下,介绍一下决策边界(Decision Boundary)的概念,这将会有助于我们能更好的理解LR的假设函数究竟是在计算什么。
在上节我们了解到逻辑回归的假设函数可以表示为
![]() ,其中
,其中![]()
在LR模型中我们知道:当假设函数![]() ,即
,即![]() ,此时我们预测成正类;反之预测为负类。由图来看,我们可以得到更加清晰的认识。下图为Sigmoid函数,也是LR的外层函数。我们看到当
,此时我们预测成正类;反之预测为负类。由图来看,我们可以得到更加清晰的认识。下图为Sigmoid函数,也是LR的外层函数。我们看到当![]() 时,此时
时,此时![]() (即内层函数
(即内层函数![]() ),然而此时也正是将y预测为1的时候;同理,我们可以得出内层函数
),然而此时也正是将y预测为1的时候;同理,我们可以得出内层函数![]() 时,我们将其预测成0(即负类)。
时,我们将其预测成0(即负类)。
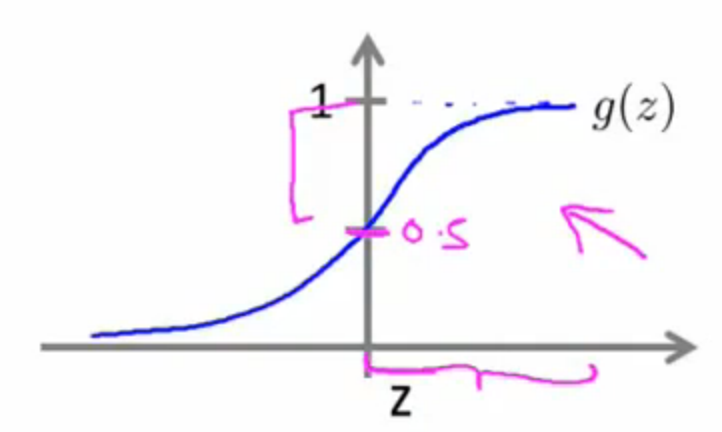
于是我们得到了这样的关系式:

这一步应该明白吧,不明白再回去看一看,它对于我们后面的理解非常重要!下面我们再举一个例子,假设我们有许多样本,并在图中表示出来了,并且假设我们已经通过某种方法求出了LR模型的参数(如下图)。
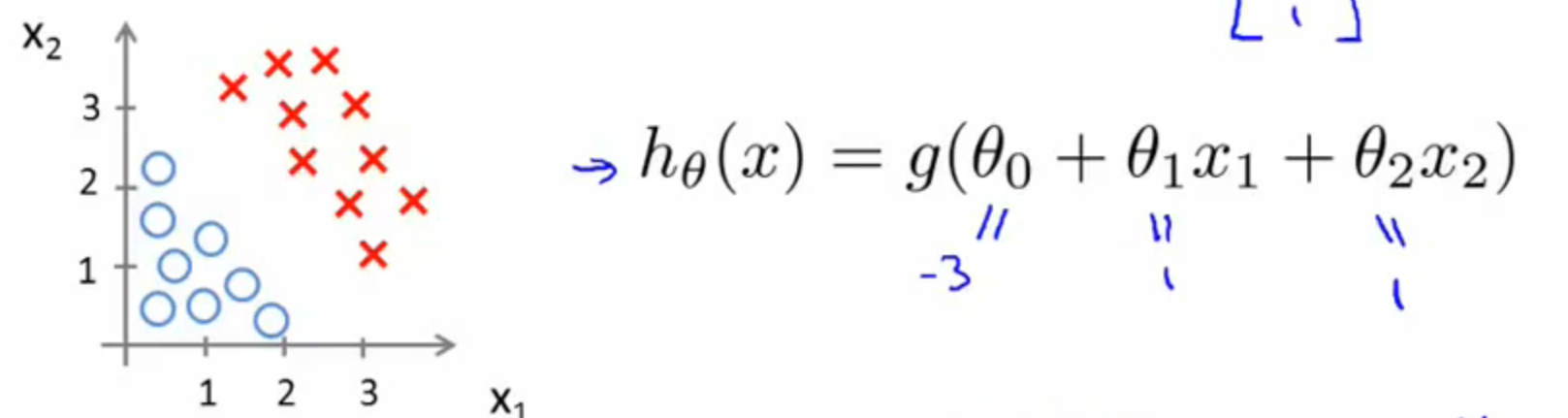
根据上面得到的关系式,我们可以得到:

而![]() 我们再图像上画出得到:
我们再图像上画出得到:
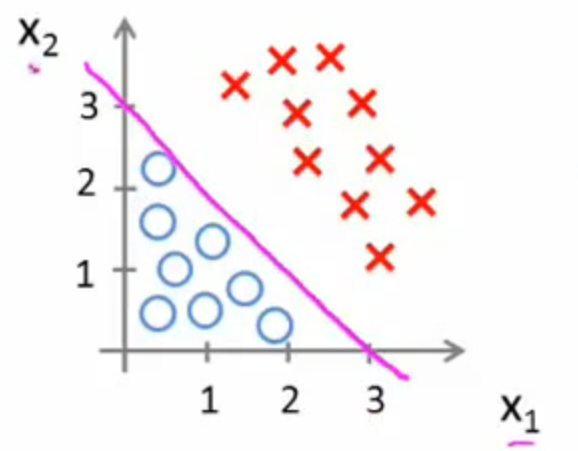
这时,直线上方所有样本都是正样本y=1,直线下方所有样本都是负样本y=0。因此我们可以把这条直线成为决策边界。
同理,对于非线性可分的情况,我们只需要引入多项式特征就可以很好的去做分类预测,如下图:
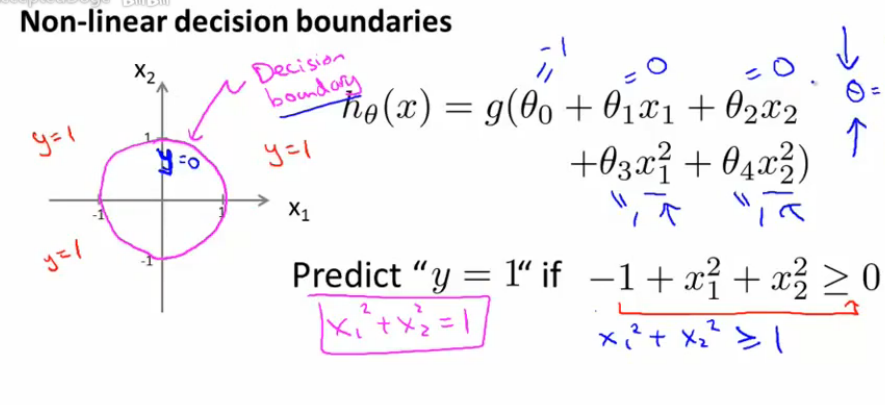
值得注意的一点,决策边界并不是训练集的属性,而是假设本身和参数的属性。因为训练集不可以定义决策边界,它只负责拟合参数;而只有参数确定了,决策边界才得以确定。
LR回归给我的直观感受就是 它利用Sigmoid的一些性质,使得线性回归(多项式回归)从拟合数据神奇的转变成了拟合数据的边界,使其更加有助于分类!就一个感触:NB!
2. 权值求解
2.1 代价函数(似然函数)
前面我们介绍线性回归模型时,给出了线性回归的代价函数的形式(误差平方和函数),具体形式如下:
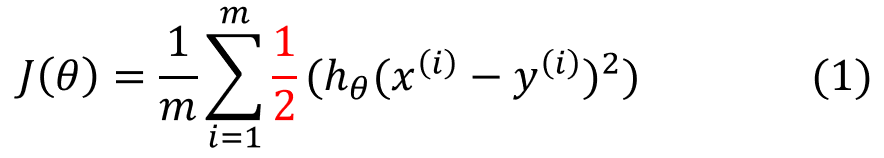
这里我们想到逻辑回归也可以视为一个广义的线性模型,那么线性模型中应用最广泛的代价函数-误差平方和函数,可不可以应用到逻辑回归呢?首先告诉你答案:是不可以的! 那么为什么呢? 这是因为LR的假设函数的外层函数是Sigmoid函数,Sigmoid函数是一个复杂的非线性函数,这就使得我们将逻辑回归的假设函数![]() 带入 (1)式时,我们得到的
带入 (1)式时,我们得到的![]() 是一个非凸函数,如下图:
是一个非凸函数,如下图:
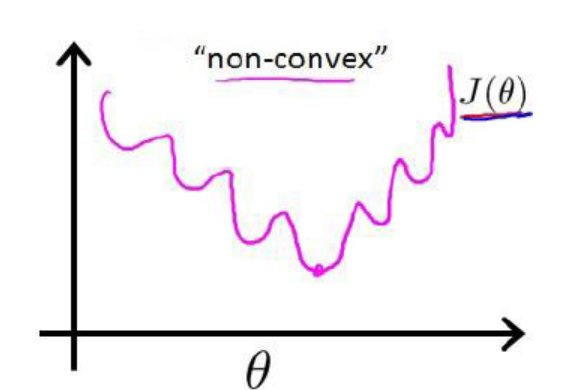
这样的函数拥有多个局部极小值,这就会使得我们在使用梯度下降法求解函数最小值时,所得到的结果并非总是全局最小,而有更大的可能得到的是局部最小值。这样解释应该理解了吧。
虽然前面的解释否定了我们猜想,但是也给我们指明了思路,那就是我们现在要做的就是为LR找到一个凸的代价函数! 在逻辑回归中,我们最常用的损失函数为对数损失函数,对数损失函数可以为LR提供一个凸的代价函数,有利于使用梯度下降对参数求解。为什么对数函数可以做到这点呢? 我们先看一下对数函数的图像:

蓝色的曲线表示的是对数函数的图像,红色的曲线表示的是负对数![]() 的图像,该图像在0-1区间上有一个很好的性质,如图粉红色曲线部分。在0-1区间上当z=1时,函数值为0,而z=0时,函数值为无穷大。这就可以和代价函数联系起来,在预测分类中当算法预测正确其代价函数应该为0;当预测错误,我们就应该用一个很大代价(无穷大)来惩罚我们的学习算法,使其不要轻易预测错误。这个函数很符合我们选择代价函数的要求,因此可以试着将其应用于LR中。对数损失在LR中表现形式如下:
的图像,该图像在0-1区间上有一个很好的性质,如图粉红色曲线部分。在0-1区间上当z=1时,函数值为0,而z=0时,函数值为无穷大。这就可以和代价函数联系起来,在预测分类中当算法预测正确其代价函数应该为0;当预测错误,我们就应该用一个很大代价(无穷大)来惩罚我们的学习算法,使其不要轻易预测错误。这个函数很符合我们选择代价函数的要求,因此可以试着将其应用于LR中。对数损失在LR中表现形式如下:

对于惩罚函数Cost的这两种情况:
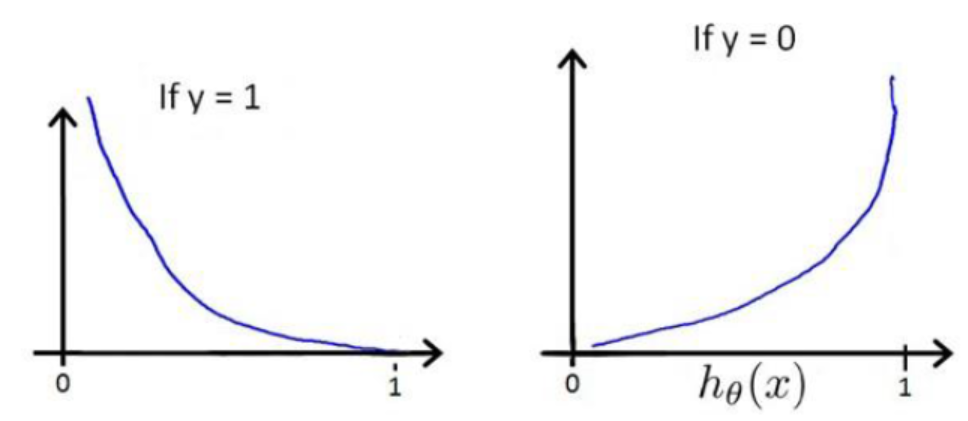
给我们的直观感受就是:当实际标签和预测结果相同时,即y和![]() 同时为1或0,此时代价最小为0; 当实际标签和预测标签恰好相反时,也就是恰好给出了错误的答案,此时惩罚最大为正无穷。现在应该可以感受到对数损失之于LR的好了。
同时为1或0,此时代价最小为0; 当实际标签和预测标签恰好相反时,也就是恰好给出了错误的答案,此时惩罚最大为正无穷。现在应该可以感受到对数损失之于LR的好了。
为了可以更加方便的进行后面的参数估计求解,我们可以把Cost表示在一行:
![]()
这与我们之前给出的两行表示的形式是等价的。因此,我们的代价函数最终形式为:

该函数是一个凸函数,这也达到了我们的要求。这也是LR代价函数最终形式。
2.2 似然函数的求解-梯度下降
前面我们得到了LR代价函数的表示形式,接下来要做的就是使用梯度下降估计参数值或参数组合。
梯度下降算法我们之前介绍过了:
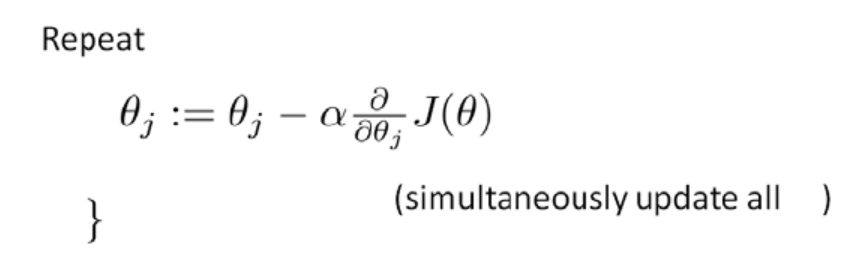
通过求导,我们得到:
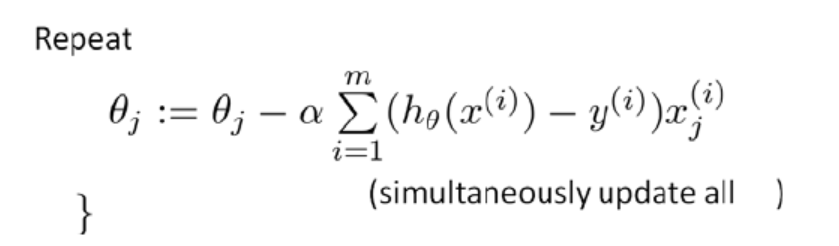
咋一看,LR的梯度下降算法和线性回归算法的形式一样呀! 没错,表现形式就是一样,但是由于假设函数![]() 的不同,注定了它们就是不同的算法。代价函数的求导过程是怎么样的呢?--- 请翻到第4部分 【代价函数的求导过程】!
的不同,注定了它们就是不同的算法。代价函数的求导过程是怎么样的呢?--- 请翻到第4部分 【代价函数的求导过程】!
3. LR模型优缺点分析
优点:
1. 实现简单,广泛应用于工业界。
2. 输出结果并不是一个离散值或确切的类型,而是一个与每个输入样本相关的概率列表,这样我们可以任意设定阈值,从而得到我们想要的分类输入。
3. LR对数据中的小噪音的鲁棒性很好,并且轻微的多重共线性不会对其结果产生特别的影响。严重的多重共线性可以使用LR+l2正则来解决。
缺点:
1. 当样本量很大时,LR的性能并不是很好。
2. 不能很好的处理大量的多类特征和变量。
3. 容易欠拟合
4. 传统的LR只能处理二分类,在此基础上衍生的Softmax才能处理多分类。
5. 对于非线性特征,需要进行转换。
总结: 知道了LR有什么优缺点了,那么我们什么情况下,最应该选择LR模型作为我们的分类预测算法呢?
应用条件有:
1. 当你需要一个概率的框架时
2. 当你希望以后可以将更多的训练数据快速整合到模型中去时
满足这两点应用条件,那就选择LR吧。
4. 代价函数的求导过程
Sigmoid函数的求导过程:

故,sigmoid函数的导数
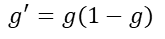
损失函数梯度求解过程:
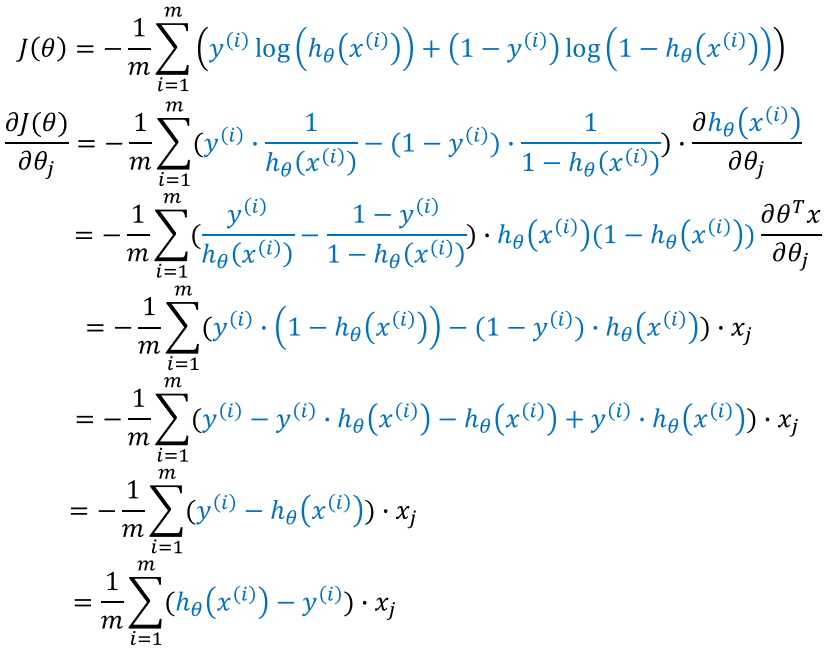
故,参数更新公式为: