一:原始信号
从音频文件中读取出来的原始语音信号通常称为raw waveform,是一个一维数组,长度是由音频长度和采样率决定,比如采样率Fs为16KHz,表示一秒钟内采样16000个点,这个时候如果音频长度是10秒,那么raw waveform中就有160000个值,值的大小通常表示的是振幅。
二:(线性)声谱图
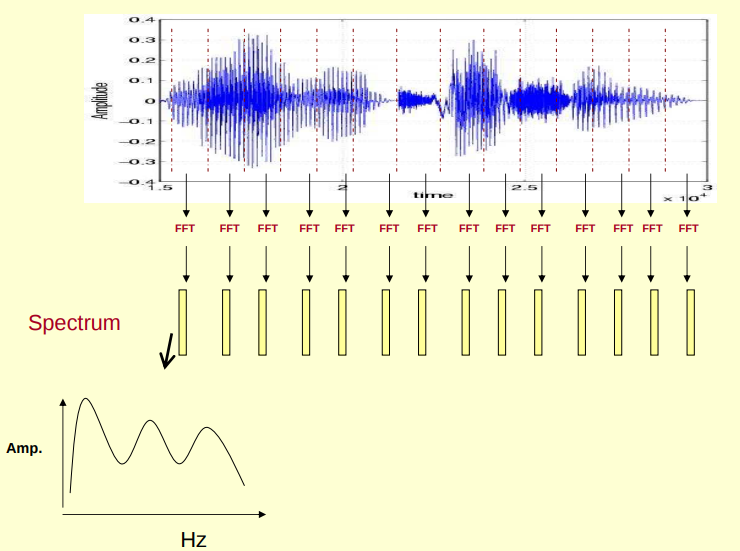
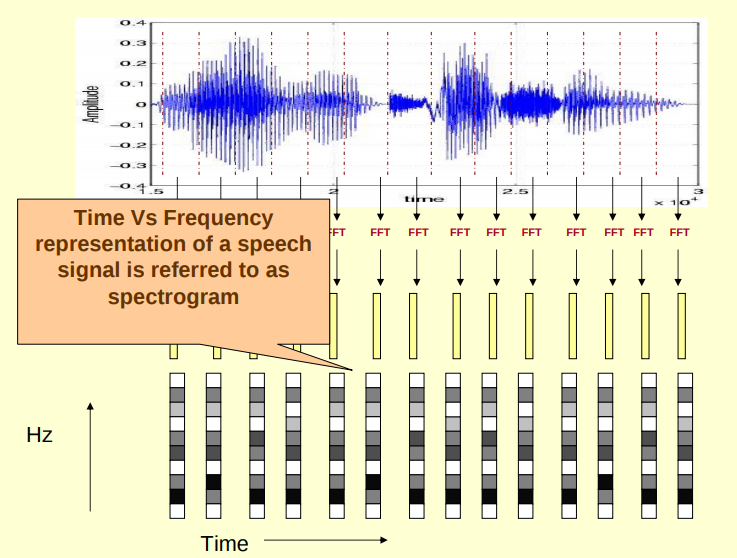
(1)对原始信号进行分帧加窗后,可以得到很多帧,对每一帧做FFT(快速傅里叶变换),傅里叶变换的作用是把时域信号转为频域信号,把每一帧FFT后的频域信号(频谱图)在时间上堆叠起来就可以得到声谱图,其直观理解可以形象地表示为以下几个图,图源见参考资料[1]。
(2)有些论文提到的DCT(离散傅里叶变换)和STFT(短时傅里叶变换)其实是差不多的东西。STFT就是对一系列加窗数据做FFT。而DCT跟FFT的关系就是:FFT是实现DCT的一种快速算法。
(3)FFT有个参数N,表示对多少个点做FFT,如果一帧里面的点的个数小于N就会zero-padding到N的长度。对一帧信号做FFT后会得到N点的复数,这个点的模值就是该频率值下的幅度特性。每个点对应一个频率点,某一点n(n从1开始)表示的频率为(F_n = (n-1)*Fs/N),第一个点(n=1,Fn等于0)表示直流信号,最后一个点N的下一个点(n=N+1,Fn=Fs时,实际上这个点是不存在的)表示采样频率Fs。
(4)FFT后我们可以得到N个频点,频率间隔(也叫频率分辨率或)为 Fs / N,比如,采样频率为16000,N为1600,那么FFT后就会得到1600个点,频率间隔为10Hz,FFT得到的1600个值的模可以表示1600个频点对应的振幅。因为FFT具有对称性,当N为偶数时取N/2+1个点,当N为奇数时,取(N+1)/2个点,比如N为512时最后会得到257个值。
(5)用python_speech_feature库时可以看到有三种声谱图,包括振幅谱,功率谱(有些资料称为能量谱,是一个意思,功率就是单位时间的能量),log功率谱。振幅谱就是fft后取绝对值。功率谱就是在振幅谱的基础上平方然后除以N。log功率谱就是在功率谱的基础上取10倍lg,然后减去最大值。得到声谱图矩阵后可以通过matplotlib来画图。
(6)常用的声谱图都是STFT得到的,另外也有用CQT(constant-Q transform)得到的,为了区分,将它们分别称为STFT声谱图和CQT声谱图。

三:梅尔声谱图:
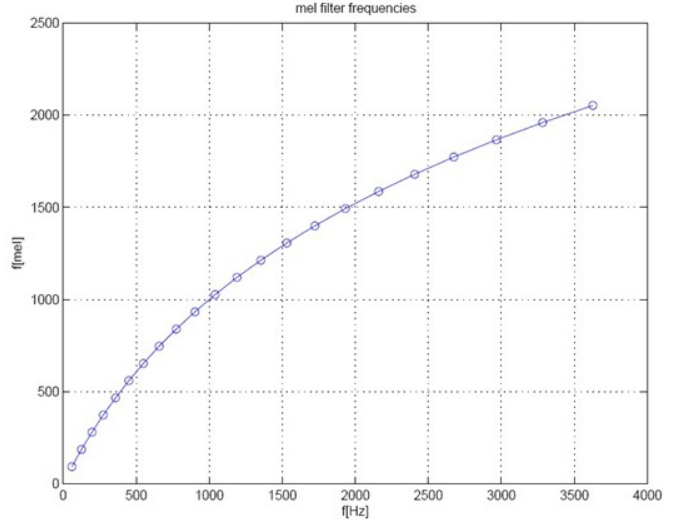
(1)人耳听到的声音高低和实际(Hz)频率不呈线性关系,用Mel频率更符合人耳的听觉特性(这正是用Mel声谱图的一个动机,由人耳听力系统启发),即在1000Hz以下呈线性分布,1000Hz以上呈对数增长,Mel频率与Hz频率的关系为(f_{mel} = 2595 cdot lg(1+frac{f}{700Hz})),如下图所示,图源见参考资料[2]。有另一种计算方式为(f_{mel} = 1125 cdot ln(1+frac{f}{700Hz}))。下面给出一个计算Mel声谱图的例子。另,python中可以用librosa调包得到梅尔声谱图。
(2)假设现在用10个Mel filterbank(一些论文会用40个,如果求MFCC一般是用26个然后在最后取前13个),为了获得filterbanks需要选择一个lower频率和upper频率,用300作为lower,8000作为upper是不错的选择。如果采样率是8000Hz那么upper频率应该限制为4000。然后用公式把lower和upper转为Mel频率,我们使用上述第二个公式(ln那条),可以得到401.25Mel 和 2834.99Mel。
(3)因为用10个滤波器,所以需要12个点来划分出10个区间,在401.25Mel和2834.99Mel之间划分出12个点,m(i) = (401.25, 622.50, 843.75, 1065.00, 1286.25, 1507.50, 1728.74, 1949.99, 2171.24, 2392.49, 2613.74, 2834.99)。
(4)然后把这些点转回Hz频率,h(i) = (300, 517.33, 781.90, 1103.97, 1496.04, 1973.32, 2554.33, 3261.62, 4122.63, 5170.76, 6446.70, 8000)。
(5)把这些频率转为fft bin,f(i) = floor( (N+1)*h(i)/Fs),N为FFT长度,默认为512,Fs为采样频率,默认为16000Hz,则f(i) = (9, 16, 25, 35, 47, 63, 81, 104, 132, 165, 206, 256)。这里256刚好对应512点FFT的8000Hz。
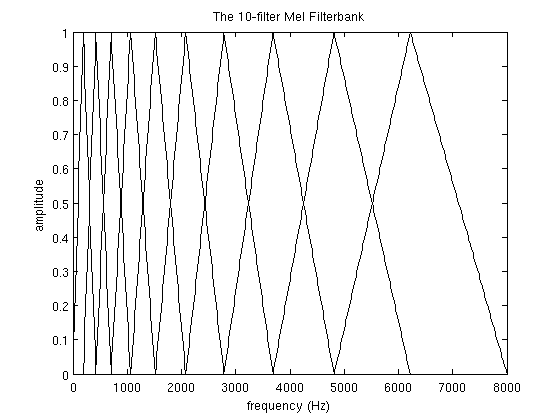
(6)然后创建滤波器,第一个滤波器从第一个点开始,在第二个点到达最高峰,第三个点跌回零。第二个滤波器从第二个点开始,在第三个点到达最大值,在第四个点跌回零。以此类推。滤波器的示意图如下图所示,图源见参考资料[3]。可以看到随着频率的增加,滤波器的宽度也增加。
(7)接下来给出滤波器输出的计算公式,如下所示,其中m从1到M,M表示滤波器数量,这里是10。k表示点的编号,一个fft内256个点,k从1到256,表示了fft中的256个频点(k=0表示直流信号,算进来就是257个频点,为了简单起见这里省略k=0的情况)。
(8)最后还要乘上fft计算出来的能量谱,关于能量谱在前一节(线性)声谱图中已经讲过了。将滤波器的输出应用到能量谱后得到的就是梅尔谱,具体应用公式如下,其中(|X(k)|^2)表示能量谱中第k个点的能量。以每个滤波器的频率范围内的输出作为权重,乘以能量谱中对应频率的对应能量,然后把这个滤波器范围内的能量加起来。举个例子,比如第一个滤波器负责的是9和16之间的那些点(在其它范围的点滤波器的输出为0),那么只对这些点对应的频率对应的能量做加权和。
(9)这样计算后,对于一帧会得到M个输出。经常会在论文中看到说40个梅尔滤波器输出,指的就是这个(实际上前面说的梅尔滤波器输出是权重H,但是这里的意思应该是将滤波器输出应用到声谱后得到的结果,根据上下文可以加以区分)。然后在时间上堆叠多个“40个梅尔滤波器输出”就得到了梅尔尺度的声谱(梅尔谱),如果再取个log,就是log梅尔谱,log-Mels。
(10)把滤波器范围内的能量加起来,可以解决一个问题,这个问题就是人耳是很难理解两个靠的很近的线性频率(就是和梅尔频率相对应的赫兹频率)之间不同。如果把一个频率区域的能量加起来,只关心在每个频率区域有多少能量,这样人耳就比较能区分,我们希望这种方式得到的(Mel)声谱图可以更加具有辨识度。最后取log的motivation也是源于人耳的听力系统,人对声音强度的感知也不是线性的,一般来说,要使声音的音量翻倍,我们需要投入8倍的能量,为了把能量进行压缩,所以取了log,这样,当x的log要翻倍的话,就需要增加很多的x。另外一个取log的原因是为了做倒谱分析得到MFCC,具体细节见下面MFCC的介绍。
四:MFCC
(1)MFCC,梅尔频率的倒谱系数,是广泛应用于语音领域的特征,在这之前常用的是线性预测系数Linear Prediction Coefficients(LPCs)和线性预测倒谱系数(LPCCs),特别是用在HMM上。
(2)先说一下获得MFCC的步骤,首先分帧加窗,然后对每一帧做FFT后得到(单帧)能量谱(具体步骤见上面线性声谱图的介绍),对线性声谱图应用梅尔滤波器后然后取log得到log梅尔声谱图(具体步骤见上面梅尔声谱图的介绍),然后对log滤波能量(log梅尔声谱)做DCT,离散余弦变换(傅里叶变换的一种),然后保留第二个到第13个系数,得到的这12个系数就是MFCC。
(3)然后再大致说说MFCC的含义,下图第一个图(图源见参考资料[1])是语音的频谱图,峰值是语音的主要频率成分,这些峰值称为共振峰,共振峰携带了声音的辨识(相当于人的身份证)。把这些峰值平滑地连起来得到的曲线称为频谱包络,包络描述了携带声音辨识信息的共振峰,所以我们希望能够得到这个包络来作为语音特征。频谱由频谱包络和频谱细节组成,如下第二个图(图源见参考资料[1])所示,其中log X[k]代表频谱(注意图中给出的例子是赫兹谱,这里只是举例子,实际我们做的时候通常都是用梅尔谱),log H[k]代表频谱包络,log E[k]代表频谱细节。我们要做的就是从频谱中分离得到包络,这个过程也称为倒谱分析,下面就说说倒谱分析是怎么做的。

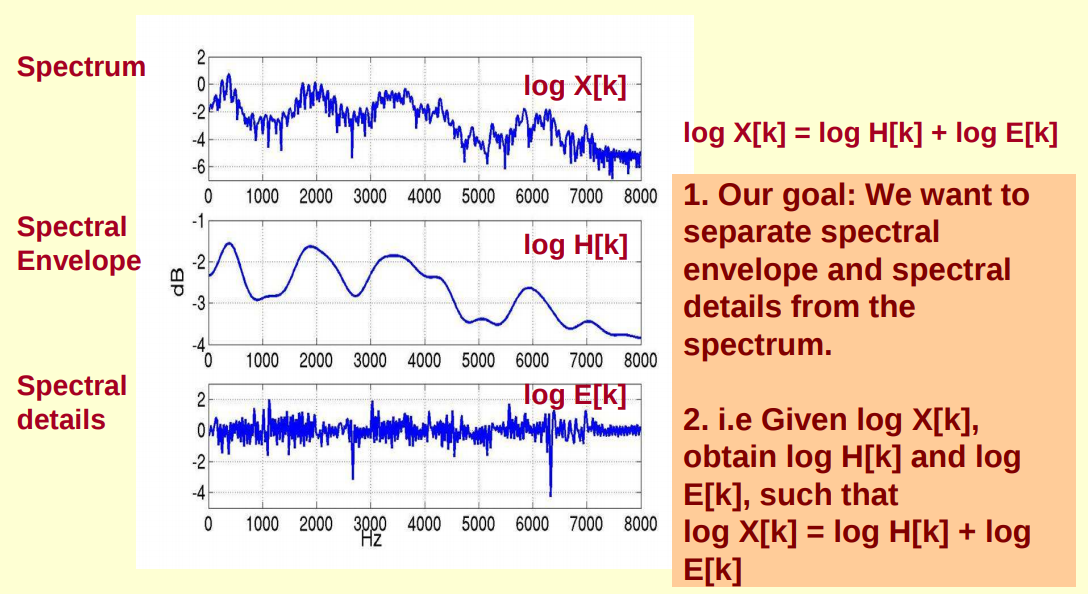
(4)要做的其实就是对频谱做FFT,在频谱上做FFT这个操作称为逆FFT,需要注意的是我们是在频谱的log上做的,因为这样做FFT后的结果x[k]可以分解成h[k]和e[k]的和。我们先看下图(图源见参考资料[1]),对包络log H[k]做IFFT的结果,可以看成“每秒4个周期的正弦波”,于是我们在伪频率轴上的4Hz上给一个峰值,记作h[k]。对细节log E[k]做IFFT的结果,可以看成“每秒100个周期的正弦波”,于是我们在伪频率轴上的100Hz上给一个峰值,记作e[k]。对频谱log X[k]做IFFT后的结果记作x[k],这就是我们说的倒谱,它会等于h[k]和e[k]的叠加,如下第二个图所示。我们想要得到的就是包络对应的h[k],而h[k]是x[k]的低频部分,只需要对x[k]取低频部分就可以得到了。
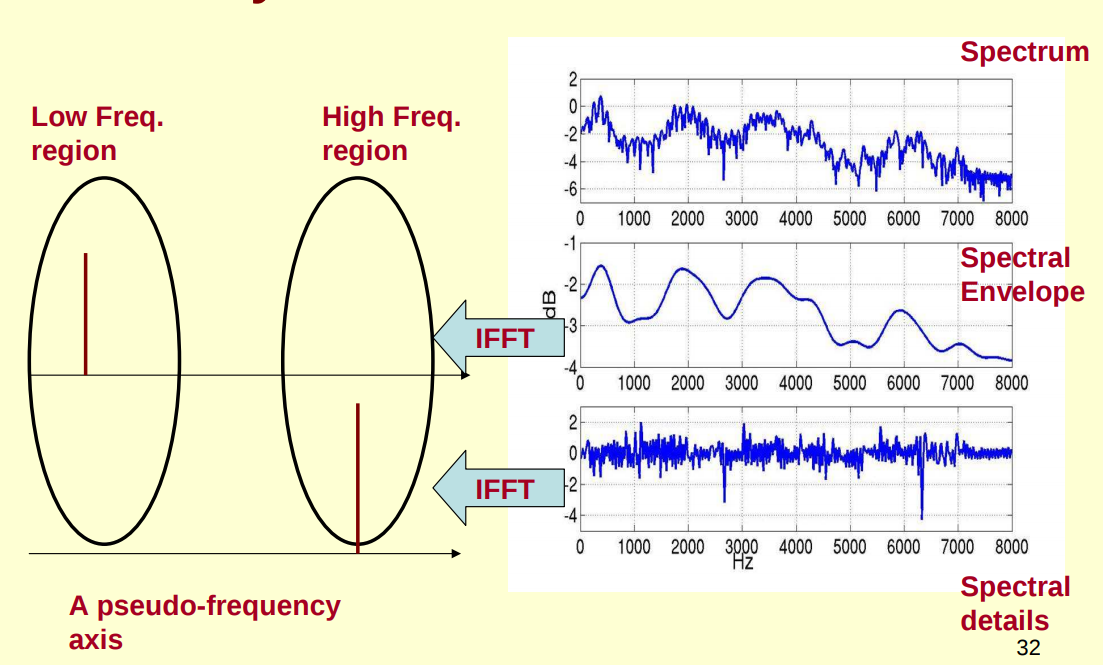

(5)最后再总结一下得到MFCC的步骤,求线性声谱图,做梅尔滤波得到梅尔声谱图,求个log得到log梅尔谱,做倒谱分析也就是对log X[k]做DCT得到x[k],取低频部分就可以得到倒谱向量,通常会保留第2个到第13个系数,得到12个系数,这12个系数就是常用的MFCC。图源见参考资料[1]。

五:deltas,deltas-deltas
(1)deltas和deltas-deltas,看到很多人翻译成一阶差分和二阶差分,也被称为微分系数和加速度系数。使用它们的原因是,MFCC只是描述了一帧语音上的能量谱包络,但是语音信号似乎有一些动态上的信息,也就是MFCC随着时间的改变而改变的轨迹。有证明说计算MFCC轨迹并把它们加到原始特征中可以提高语音识别的表现。
(2)以下是deltas的一个计算公式,其中t表示第几帧,N通常取2,c指的就是MFCC中的某个系数。deltas-deltas就是在deltas上再计算以此deltas。
(3)对MFCC中每个系数都做这样的计算,最后会得到12个一阶差分和12个二阶差分,我们通常在论文中看到的“MFCC以及它们的一阶差分和二阶差分”指的就是这个。
(4)值得一提的是deltas和deltas-deltas也可以用在别的参数上来表述动态特性,有论文中是直接在log Mels上做一阶差分和二阶差分的,论文笔记:语音情感识别(二)声谱图+CRNN中3-D Convolutional Recurrent Neural Networks with Attention Model for Speech Emotion Recognition这篇论文就是这么做的。
六:参考资料
[1] CMU语音课程slides
[2] 一个MFCC的介绍教程
[3] csdn-MFCC计算过程
[4] 博客园-MFCC学习笔记