算法复杂度

序

    算法的复杂性体现在运行该算法时所需的计算机资源多少，而计算机资源最重要的是时间和空间。算法复杂度分为时间复杂度和空间复杂度。

    一个高级语言编写的程序在计算机上运行所消耗的时间取决于下列因素：

        1、算法采用的策略、方案

        2、编译产生的代码质量

        3、问题的输入规模

        4、机器执行指令的速度

   抛开与计算机硬件、软件有关的因素，一个程序的运行时间依赖于算法的好坏和问题的输入规模。

时间复杂度

  时间频度

     一个算法中的语句执行次数。记为T(n);

  时间复杂度

     时间频度中，n称为问题的规模，当n不断变化时，时间频度T(n)也会不断变化。为了知道变化时呈现什么规律，引入时间复杂度。

    若存在某个函数f(n)，当 n –> ∞时，T(n) / f(n) 为不等于0的常数，则称f(n)是T(n)的同数量级函数。记为T(n) = O(f(n))；称O(f(n))为算法的渐进时间复杂度，简称时间复杂度。

     随之n的增大，时间的增长率和f(n)的增长率成正比。f(n)越小，算法的时间复杂度越低，算法的效率越高。

  最坏时间复杂度

     最坏情况下的时间复杂度称为最坏时间复杂度。最坏情况下的时间复杂度是算法在任何输入实例上运行时间的上界。

     不特别说明的情况下，讨论的时间复杂度即为最坏时间复杂度。

  平均时间复杂度

     所有可能的输入实例均以等概率出现的情况下，算法的期望运行时间。

空间复杂度

     算法所耗费的存储空间，记为S(n);

     一个算法在计算机存储器上所占用的存储空间包括三个方面：

     1、存储算法本身所占用的存储空间；

          与算法书写的长短成正比，要压缩此方面的存储空间，则必须编写出精短的算法。

     2、算法的输入输出数据所占用的存储空间；

          由解决的问题决定，是通过参数表由调用函数传递而来，不随算法的不同而改变。

     3、算法在运行过程中临时占用的存储空间；

          随算法的不同而不同。主要包括动态分配的空间、以及递归栈所需的空间等。

     一个算法的空间复杂度只考虑在运行过程中为局部变量分配的存储空间的大小，它包括为参数表中形参变量分配的存储空间和为在函数体中定义的局部变量分配的存储空间两个部分。

源码分析

     以 1+2+3+4+5+6+……+100 为例：

     累加：

int i, sum = 0, n = 100;   // 执行1次
for( i = 1; i <= n; i++ )  // 执行了n+1次
{
    sum = sum + i;         // 执行n次
   5:  }

     高斯算法：

int sum = 0, n = 100;     // 执行1次
sum = ( 1 + n ) * n / 2;  // 执行1次

     把循环看做一个整体，忽略头尾判断的开销，累加与高斯算法之间其实就是n和1的差距。

     循环判断在累加里面执行了n+1次，是个不小的数量，为什么忽略呢？我们研究算法的复杂度，侧重研究的是随着输入规模扩大，增长量的一个抽象，而不是精确的定位需要执行多少次。也就是说我们的研究是基于数量级的判断，而不是精确值的判断。

     比如：

int i, j, x = 0, sum = 0, n = 100;
for( i = 1; i <= n; i++ )
{
    for( j = 1; j <= n; j++ )
    {
        x++;
        sum = sum + x;
    }
}

     我们判断需要执行n^2次。

 

  

     分析一个算法的运行时间，重要的是建立基本操作的数量与输入模式的关系。判断一个算法效率时，函数中的常数和其他次要项常常可以忽略，而更应注意最高项的阶数。

   按数量级递增排序，常见的时间复杂度有：

       1、常数阶O(1)

       2、对数阶O(log(2)n)

       3、线性阶O(n)

       4、线性对数阶O(nlog(2)n)

       5、平方阶O(n^2),立方阶O(n^3),……，

       6、K次方阶O(n^k)

       7、指数阶O(2^n)

       8、阶乘O(n!)

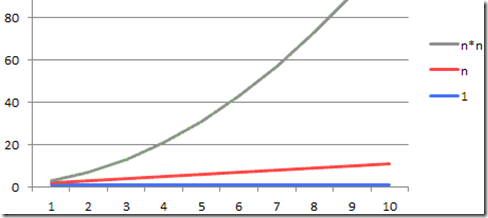
   随着问题规模n的不断增大，上述时间复杂度不断增大，算法的执行效率越低。

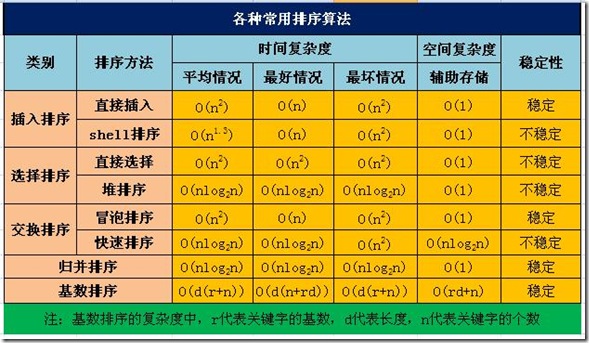
各类排序算法时间复杂度和空间复杂度对比表