3.1高级语言和机器指令中的运算
3.1.1 C程序中涉及的运算
•按位运算:符号|表示按位OR运算;符号&表示按位AND运算;符号~表示按位NOT运算;符号^表示按位XOR运算。
•逻辑运算:符号||表示按位OR运算;符号&&按位AND运算;符号!表示按位NOT运算。
•移位运算:有逻辑移位和算术移位两种。逻辑移位不考虑符号位,总是把高(低)移出,低(高)位补0。
•位扩展和位截断运算:进行数据类型转换时,如果遇到一个短数向长数转换,就要进行位扩展运算。进行位扩展运算时,扩展后的数值应保持不变。有两种位扩展方式:0扩展和符号扩展。
3.2基本运算部件
基本的运算部件是加法器、ALU和移位器、ALU的核心部件是加法器。
3.2.1 串进位加法器
全加器用来实现两个本位数加上低位进行生成一位本位以及一位向高位的进位。第i位的加法运算是指第i位的加数Xi、Yi和低位来的进位Ci-1三者相加,得到本体和Fi和第i位的进位输出Ci。
3.2.3 带标志加法器
n位无符号数加法器只能用于两个n位二进制数相加,不能进行无符号整数的减法运算,也不能进行带符号整数的减法运算
3.3定点运算
3.3.1 补码加减运算
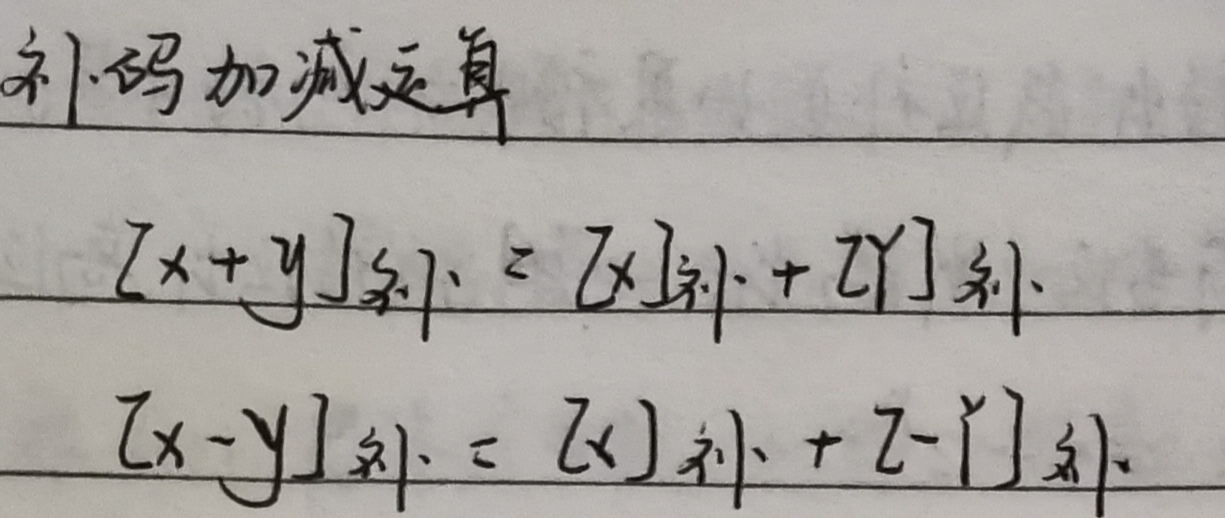
3.3.2 原码加减运算
•比较两个操作数的符号,对加法实行“同号求和,异号求差”,对减法实行“异号求和,同号求差”。
•求和时,数值位相加,若最高位产生进位则结果溢出。和的符号位取被加数(被减数)的符号。
•求差时,被加数(被减数)数值位加上加数(减数)数值位的补码。
3.3.3 移码加减运算:移码的和、差等于和、差的补码。
3.3.4 原码乘法运算
•原码一位乘法
a.确定乘积的符号位,由两个乘数的符号异或得到。
b.计算乘积的数值位,乘积的数值部分为两个乘数的数值部分之积。
•原码二位乘法
对乘数的每两位取值情况进行判断,使每步求出对应于该两位的部分积,则可将乘法速度提高一倍
3.3.5 补码乘法运算
•补码一位乘法
布斯乘法:将符号位和数值位合在一起参与运算,直接得出用补码表示的乘积,且正数和负数同等对待。
•补码两位乘法运算速度。
3.3.6原码除法运算
只有当被除数和除数都不为0,并且商也不可能溢出时,才能进一步进行除法运算。
原码除法运算与原码乘法运算一样,要将符号位和数值位分开来处理,商的符号为相除两数符号的“异或”值,商的数值为两数绝对值之商。
•恢复余数除法
a.符号位单独处理,分别取除数和被除数绝对值进行运算(和原码两位乘一样,参与运算的是绝对值的补码)。
b.若余数(被除数)为正,表示够减,商上1,左移一位,减去[ y ] 补 [y]_补[y] 补 若余数(被除数)为负,表示不够减,商上0,恢复余数(加上除数),左移一位,加上[ − y ] 补 [-y]_补[−y] 补。
c.重复上一步骤n次(需设置一个计数器)。
d.若最后一步余数为负,需要恢复余数,否则不需要。
•不恢复余数除法
若余数(被除数)为负,表示不够减,商上0,恢复余数(加上除数) ,左移一位,加上[-y]_补 , 加上[ y ] 补 [y]_补[y] 补
###3.3.7补码除法运算
首先要对被除数和除数取值、大小等进行相应的判断,以确定除数是否为0,商是否为0,是否溢出。
根据被除数(中间余数)与除数之间符号的异同或差值的正负来确定下次做减法还是加法。
•补码恢复余数除法
a.够键则上商为1,不够减则上商为0。
b.若商为负值,则“各位取反,末位加1”来取得真正的商。
•补码不恢复余数法
a.对于小数补码运算,商等于“-1”是被允许的。
b.n位小数补码除法共上商n+1次,移位n次,和原码除法一样。
3.4 浮点数运算
3.4.1 浮点数加减运算
浮点数运算的特点是阶码运算和尾数运算分开来算。加减运算一律采用补码。
•对阶
对阶的目的是让两个数小数点的位置看齐,使这两个数的阶码相等。
•尾数加减
对阶后两个浮点数的指数相等,此时,可以进行对阶后的尾数相加减。
•尾数规格化
尾数求和后的结果需要规格化,运算结果为正数,规格化的形式应该是00.1xxx......x,为负数,规格化后的形式应该是11.0xxx......x。
•尾数的舍入处理
a.就近舍入。舍入为最近可表示的数。
b.朝+∞方向舍入。总是取右边最近的可表示数。
c.朝-∞方向舍入。总是取左边最近的可表示数。
d.朝0方向舍入。直接截取所需位数,丢弃后面所有位。
•溢出判断
溢出判断其实是在上述尾数规格化和尾数舍入过程中进行,只要涉及阶码求和/差,就可以在解码运算部件中直接用溢出判断电路来实现。
a.右规和尾数舍入。
b.左规。
3.4.2 浮点数乘除运算
•浮点数乘法运算
a.尾数相乘,指数相加。
b.尾数规格化。
c.尾数舍入处理。
d.溢出判断。
•浮点数除法运算
a.尾数相除,阶相减。
b.尾数规格化。
c.尾数舍入处理。
d.溢出判断



