Hash表是一种数据结构 提供快速的存取和查找,他是基于数组的,数组创建后大小是固定的难以拓展 ,当然可以复制数据到更大的数组,但是非常消耗性能,如果数据量固定,需要快速查询时 hash表是一个不错的选择
数组只能以数字作为下标 而不能以字符串作为下标 所以要考虑将字符串转换为唯一的数字 这个过程叫做hash化 过程由hash函数完成,使用hash函数插入数据到数组后,数组被称为hash表
Hash函数
1叠加法
假如给 字母编个号码
空格0 a 1 ,b2 c 2, 27 z
Hash函数采用加法运算
比如 abc = 1+2+3
最大的字母是10位
zzzzzzzzzz=26*10=260
显然 所有的字母可能只能组合出 260个索引为 ,而实际上单词有 50000
而每一个索引的位置 需要存放单词 50000/260=192个单词 显然不行
2 幂的连续乘法
参考数字的拆分
234=2*100+3*10+4
那么abc 因为字母是27个
1*27*27+2*27+3= 786
如果是 zzzzzzzzzz=? 不知道有多大 可能会操过变量允许的最大位数
怎么解决了 可以对产生的数字进行压缩
比如 数组的大小是1000
那么获取下标可以用 要存放的字母幂的连乘获取的结果 % 1000(也就是数组的大小)
就能获取一个数 <1000 的
比如(1000+999)%1000 =999
这样仍然有一个问题
就是数组 可能压缩产生的数字 已经被其他的字母占据了 怎么办了
有两种解决方法 :开放地址法 和 链地址法
2.1开放地址法:
开放地址法就是发现如果被占据,就需要利用方法去找寻空白的位置,三种方法:线性探测,二次探测,再hash法
线性探测: 比如产生的索引位置是123,123被占据了 找124 124被占用找125 一直到找到是空白的地址
二次探测:已填充数据的个数/hash表的大小 就是装填因子,聚集就是hash表某个部分的位置都被填充 而部分位置一个数据的都没有 出现聚集时 可能到比较远一点的单元格去寻找空的位置 就叫二次探测
一次探测 比如 找到的位置是 123 123+1 ,123+2 一步一步探测
二次探测 找到的位置是 123 123+1 123+4 123+9 已 n的平方来探测
可以这么理解 首先查找临边 如果临边被占据了 怀疑可能旁边也被占据了,跳到4的位置
有点忧虑可能有很大的聚集 结果跳到9的位置
但是二次探测也会产生问题 :二次聚集 比如 n多个数 通过hash函数转换的数字式一样的 跳动的步骤也是一样的 出现二次聚集
再哈希法:二次探测出现二次聚集的原因是因为 步长时相同的,现在需要创建一个布长不一样的探测序列 这个序列可以在用一次hash化一便,布长不能为0 否则每次都在原地打转
stepSize=contant*(key%contant)
contant是介质 小于数组容量,key是第一次hash的位置
2.2链地址法:
这种方法比较容易理解
Hash表中位置放置的是第一次插入的值,以后如果hash话出来的位置 已经存在数据的话 就已链表的形式指向第一个位置 ,如果在来一个指向第二个位置
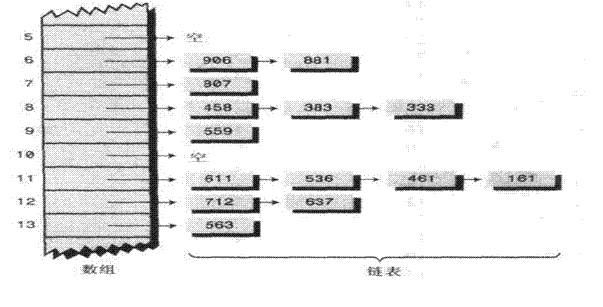
很明显这样做会出现重复值 ,当然也允许出现重复值
链表就不用再担心容量问题