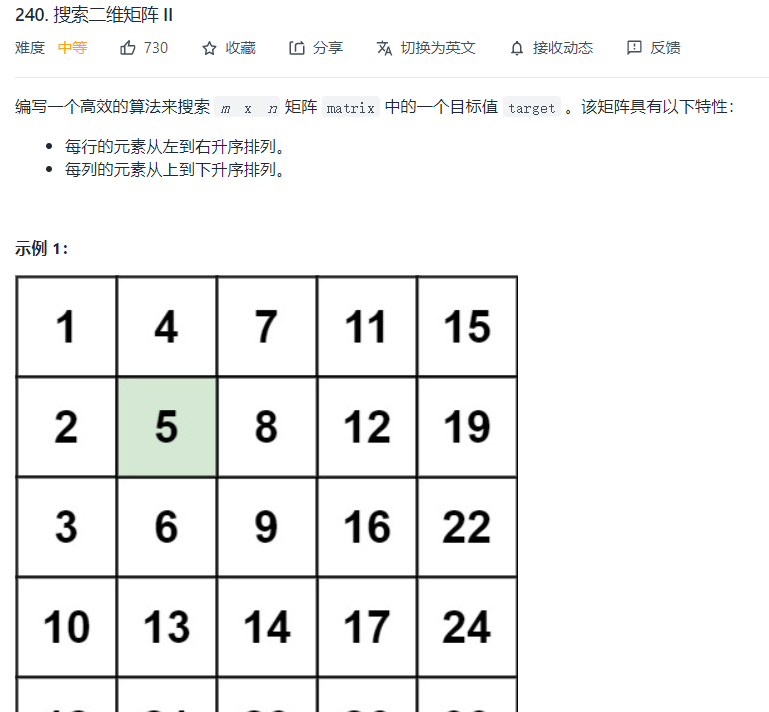
方法二:二分法搜索 矩阵已经排过序,就需要使用二分法搜索以加快我们的算法。 算法: 首先,我们确保矩阵不为空。那么,如果我们迭代矩阵对角线,从当前元素对列和行搜索,我们可以保持从当前 (row,col)(row,col) 对开始的行和列为已排序。
因此,我们总是可以二分搜索这些行和列切片。我们以如下逻辑的方式进行 : 在对角线上迭代,二分搜索行和列,直到对角线的迭代元素用完为止(意味着我们可以返回 false )
或者找到目标(意味着我们可以返回 true )。binary search 函数的工作原理和普通的二分搜索一样,但需要同时搜索二维数组的行和列。 作者:LeetCode 链接:https://leetcode-cn.com/problems/search-a-2d-matrix-ii/solution/sou-suo-er-wei-ju-zhen-ii-by-leetcode-2/ 来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
class Solution { //对每个对角线元素对应的行和列进行二分搜索 private boolean binarySearch(int[][] matrix, int target, int start, boolean vertical) { int lo = start; int hi = vertical ? matrix[0].length-1 : matrix.length-1; while (hi >= lo) { int mid = (lo + hi)/2; if (vertical) { // searching a column if (matrix[start][mid] < target) { lo = mid + 1; } else if (matrix[start][mid] > target) { hi = mid - 1; } else { return true; } } else { // searching a row if (matrix[mid][start] < target) { lo = mid + 1; } else if (matrix[mid][start] > target) { hi = mid - 1; } else { return true; } } } return false; } public boolean searchMatrix(int[][] matrix, int target) { // an empty matrix obviously does not contain `target` if (matrix == null || matrix.length == 0) { return false; } // iterate over matrix diagonals int shorterDim = Math.min(matrix.length, matrix[0].length); for (int i = 0; i < shorterDim; i++) { boolean verticalFound = binarySearch(matrix, target, i, true); boolean horizontalFound = binarySearch(matrix, target, i, false); if (verticalFound || horizontalFound) { return true; } } return false; } } 作者:LeetCode 链接:https://leetcode-cn.com/problems/search-a-2d-matrix-ii/solution/sou-suo-er-wei-ju-zhen-ii-by-leetcode-2/ 来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
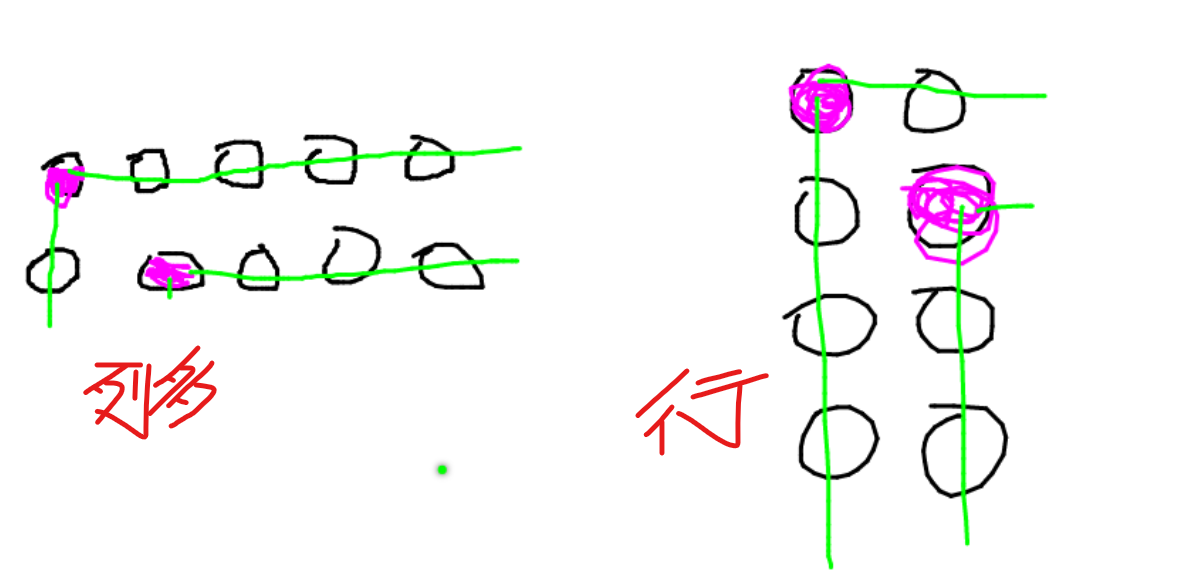
选取行和列的最小值,然后遍历对角线元素对应的行和列即可全部遍历完
方法四: 因为矩阵的行和列是排序的(分别从左到右和从上到下),所以在查看任何特定值时,我们可以修剪O(m)或O(n)元素。 算法: 首先,我们初始化一个指向矩阵左下角的 (row,col) 指针。然后,直到找到目标并返回 true(或者指针指向矩阵维度之外的(row,col) 为止,
我们执行以下操作:如果当前指向的值大于目标值,则可以 “向上” 移动一行。 否则,如果当前指向的值小于目标值,则可以移动一列。
不难理解为什么这样做永远不会删减正确的答案;因为行是从左到右排序的,所以我们知道当前值右侧的每个值都较大。
因此,如果当前值已经大于目标值,我们知道它右边的每个值会比较大。也可以对列进行非常类似的论证,因此这种搜索方式将始终在矩阵中找到目标(如果存在)。 作者:LeetCode 链接:https://leetcode-cn.com/problems/search-a-2d-matrix-ii/solution/sou-suo-er-wei-ju-zhen-ii-by-leetcode-2/ 来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
class Solution { public: bool searchMatrix(vector<vector<int>>& matrix, int target) { int p1=matrix.size()-1; int p2=0; while(p1>=0 && p2<matrix[0].size()) { if(matrix[p1][p2]>target) { p1--; } else if(matrix[p1][p2]<target) { p2++; } else{ return true; } } return false; } };