【河内之塔(汉诺塔)】

/*
说明：
河内之塔(Towers of Hanoi)是法国人M.Claus(Lucas)于1883年从泰国带至法国的，河内之塔为越战时北越的首都
，即现在的胡志明市；1883年法国数学家Edouar Lucas曾提及这个故事，据说创世纪时Benares有一座波罗教塔，
是由三支钻石棒所支撑，开始时神在第一根棒上放置64个由上至下依由小到大排列的金盘(Disc)，并命令僧侣将
所有的金盘从第一根石棒移至第三根石棒，且搬运过程中遵守大盘子在小盘子之下的原则，若每日仅搬一个盘子，
则当盘子全数搬运完毕之时，此塔将毁损，而也就是世界末日的来临之时。

解法：
如果柱子标为ABC，要由A搬至C，在只有一个盘子时，就将它直接搬至C，当有两个盘子，就将B当作辅助柱。如果
盘数超过两个，将第三个以下的盘子遮起来，就很简单了，每次处理两个盘子，也就是：A->B，A->C，B->C这三个
步骤，而被遮住的部分，其实就是进入程式的递回处理。事实上，若有n个盘子，则先移动完毕所需次数为(2^n)-1，
所以当盘数为64时，则所需次数为(2^64)-1 = 18446744073709551615为5.05390248594782e+16年，也就是约5000
世纪，如果对这数字没什么概念，就假设每秒钟搬一个盘子好了，也要5850亿年左右。 
*/

#include <stdio.h>

void hanoi(int n, int A, int B, int C)
{
    if(n == 1)
        printf("Move sheet %d from %c to %c
", n, A, C);
    else
    {
        hanoi(n-1, A, C, B);
        printf("Move sheet %d from %c to %c
", n, A, C);
        hanoi(n-1, B, A, C);
    }
}

int main(void)
{
    int n;
    printf("请输入盘数: 
");
    scanf("%d", &n);
    hanoi(n, 'A', 'B', 'C');
    return 0;
}

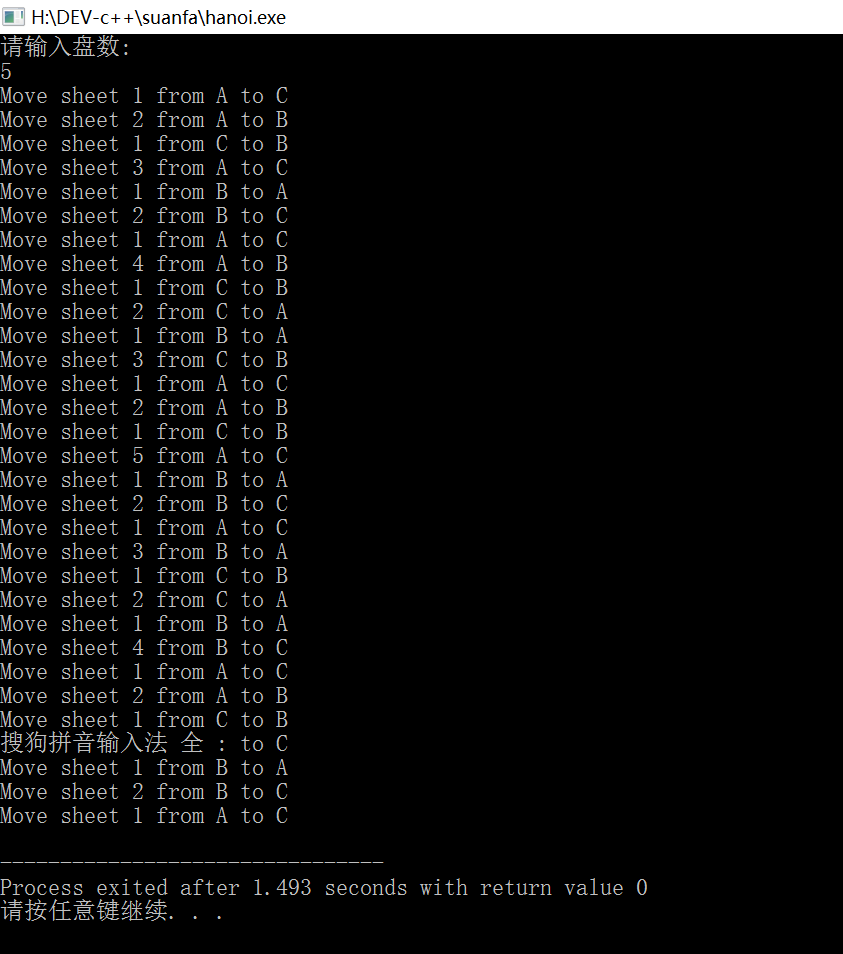
运行结果：