bzoj 2127 happiness（最小割）

【题目链接】

    http://www.lydsy.com/JudgeOnline/problem.php?id=2127

【题意】

    有n*m个学生，每个人可以选择学文学理，都会有相应的分值，而且相邻两个人如果选择相同还会产生联合分值，求最大分值。

【思路】

    建立ST，首先由S连边(S,u,a)a代表学文的分数，连向T(u,T,b)b表示学理的分数，这样构造出了两个人独立的分数。

然后考虑联合分数，对于相邻的两个点xy，看下图（盗个图：

 

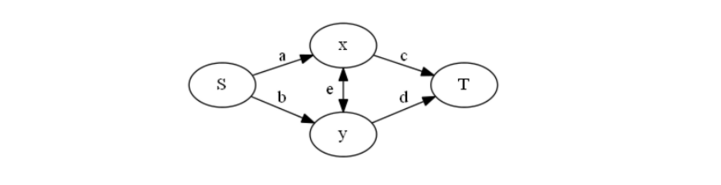
　 设xy都学文的分数为w1,都学理的分数为w2，则a=w1/2,b=w1/2,c=w2/2,d=w2/2,e=(w1+w2)/2，每一种割与其对应的亏损分数如下：

    　　a+b          -w1　　　　　　都学理->w2

    　　c+d          -w2　　　　　　都学文->w1

    　　a+d+e       -w1-w2　　　  不同->   0

    　　c+d+e       -w1-w2　　　　...

　 注意双向边e，我们是变成两条有向边加入网络，而又因为我们求最小割用的是最大流的算法，所以这条边可以看作是一条双向且权值为e的边。

　 然后把权值*2，解决精度问题。

【代码】

#include<set>
#include<cmath>
#include<queue>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define trav(u,i) for(int i=front[u];i;i=e[i].nxt)
#define FOR(a,b,c) for(int a=(b);a<=(c);a++)
using namespace std;

typedef long long ll;
const int N = 4e4+10;
const int M = 1e2+10;
const int inf = 1e9;

ll read() {
    char c=getchar();
    ll f=1,x=0;
    while(!isdigit(c)) {
        if(c=='-') f=-1; c=getchar();
    }
    while(isdigit(c))
        x=x*10+c-'0',c=getchar();
    return x*f;
}

struct Edge {
    int u,v,cap,flow;
};
struct Dinic {
    int n,m,s,t;
    int d[N],cur[N],vis[N];
    vector<int> g[N];
    vector<Edge> es;
    queue<int> q;
    void init(int n) {
        this->n=n;
        es.clear();
        FOR(i,0,n) g[i].clear();
    }
    void AddEdge(int u,int v,int w) {
        es.push_back((Edge){u,v,w,0});
        es.push_back((Edge){v,u,0,0});
        m=es.size();
        g[u].push_back(m-2);
        g[v].push_back(m-1);
    }
    int bfs() {
        memset(vis,0,sizeof(vis));
        q.push(s); d[s]=0; vis[s]=1;
        while(!q.empty()) {
            int u=q.front(); q.pop();
            FOR(i,0,(int)g[u].size()-1) {
                Edge& e=es[g[u][i]];
                int v=e.v;
                if(!vis[v]&&e.cap>e.flow) {
                    vis[v]=1;
                    d[v]=d[u]+1;
                    q.push(v);
                }
            }
        }
        return vis[t];
    }
    int dfs(int u,int a) {
        if(u==t||!a) return a;
        int flow=0,f;
        for(int& i=cur[u];i<g[u].size();i++) {
            Edge& e=es[g[u][i]];
            int v=e.v;
            if(d[v]==d[u]+1&&(f=dfs(v,min(a,e.cap-e.flow)))>0) {
                e.flow+=f; 
                es[g[u][i]^1].flow-=f;
                flow+=f; a-=f;
                if(!a) break;
            }
        }
        return flow;
    }
    int MaxFlow(int s,int t) {
        this->s=s,this->t=t;
        int flow=0;
        while(bfs()) {
            memset(cur,0,sizeof(cur));
            flow+=dfs(s,inf);
        }
        return flow;
    }
} dc;

int n,m,ans,a[M][M],b[M][M],id[M][M];

void addedge(int u,int v,int w)
{
    dc.AddEdge(u,v,w); dc.AddEdge(v,u,w);
}

int main()
{
    n=read(),m=read();
    dc.init(n*m+2);
    int S=0,T=n*m+1;
    FOR(i,1,n) FOR(j,1,m) {
        a[i][j]=read(); ans+=a[i][j];
        a[i][j]<<=1; id[i][j]=(i-1)*m+j;
    }
    FOR(i,1,n) FOR(j,1,m) {
        b[i][j]=read(); ans+=b[i][j];
        b[i][j]<<=1;
    }
    int x;
    FOR(i,1,n-1) FOR(j,1,m) {
        x=read(); a[i][j]+=x,a[i+1][j]+=x;
        ans+=x;
        addedge(id[i][j],id[i+1][j],x);
    }
    FOR(i,1,n-1) FOR(j,1,m) {
        x=read(); b[i][j]+=x,b[i+1][j]+=x;
        ans+=x;
        addedge(id[i][j],id[i+1][j],x);
    }
    FOR(i,1,n) FOR(j,1,m-1) {
        x=read(); a[i][j]+=x,a[i][j+1]+=x;
        ans+=x;
        addedge(id[i][j],id[i][j+1],x);
    }
    FOR(i,1,n) FOR(j,1,m-1) {
        x=read(); b[i][j]+=x,b[i][j+1]+=x;
        ans+=x;
        addedge(id[i][j],id[i][j+1],x);
    }
    FOR(i,1,n) FOR(j,1,m) {
        dc.AddEdge(S,id[i][j],a[i][j]);
        dc.AddEdge(id[i][j],T,b[i][j]);
    }
    printf("%d
",ans-(dc.MaxFlow(S,T)>>1));
    return 0;
}