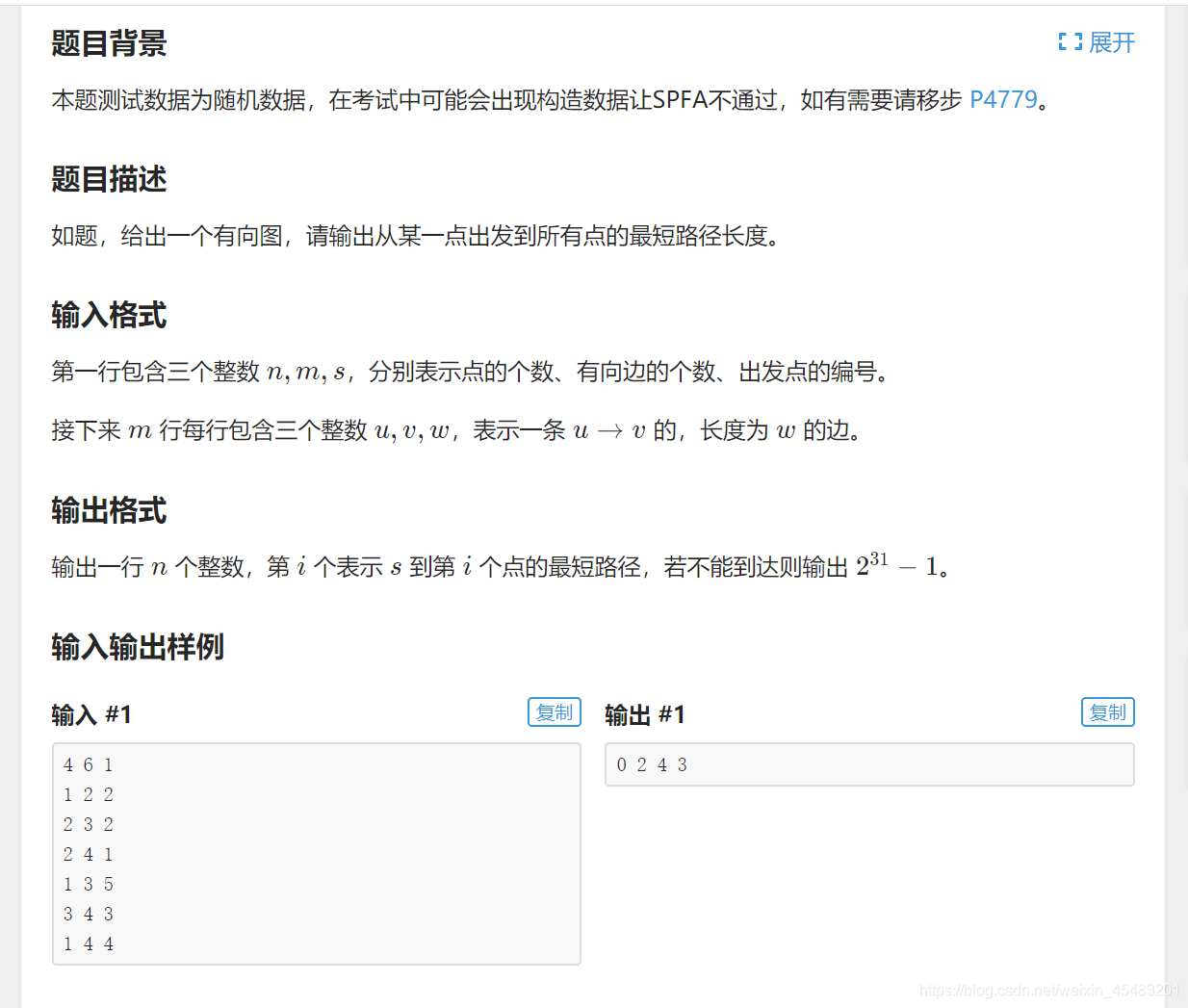
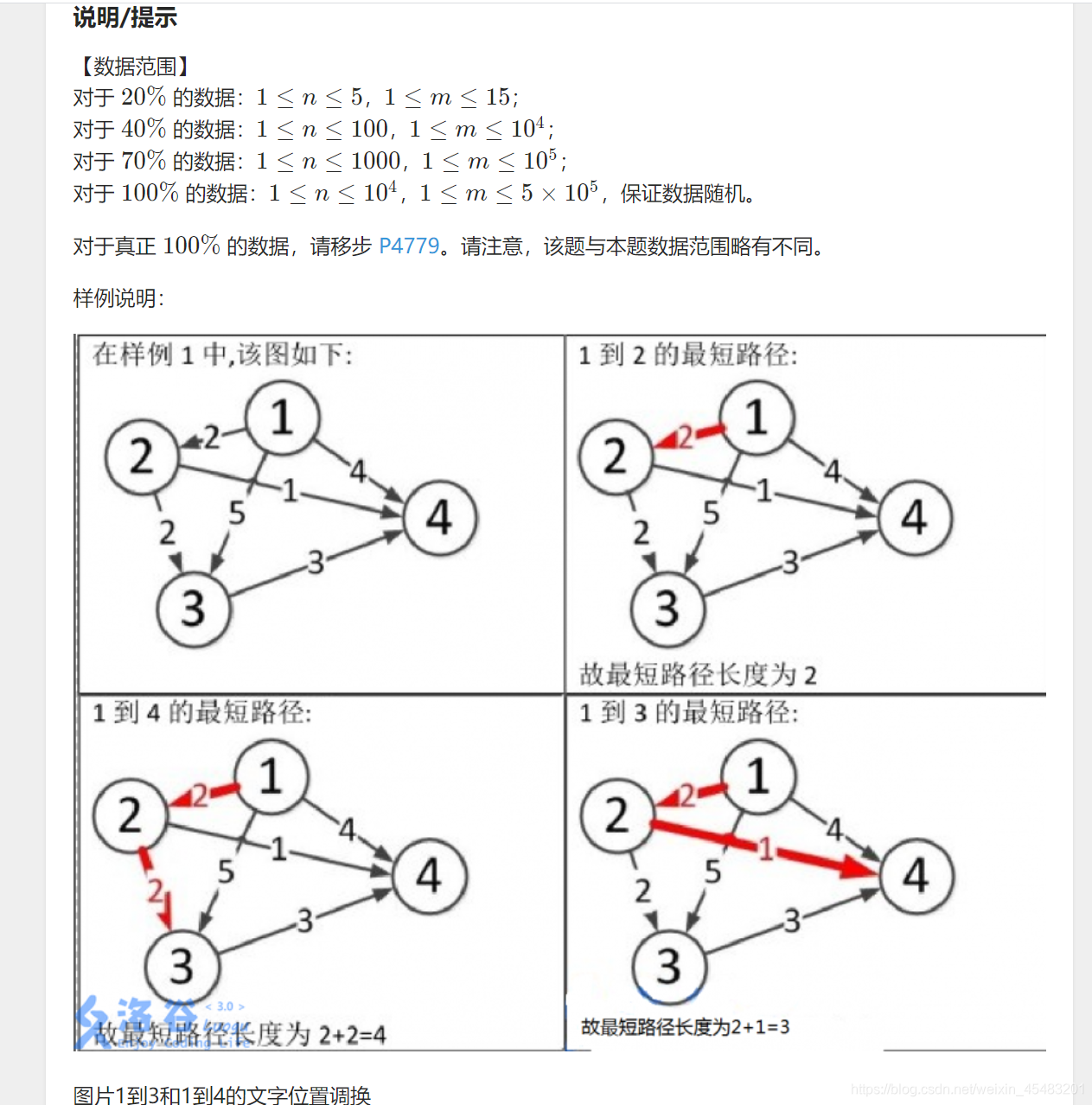
弗洛伊德算法大致有点像dp的推导
dp[i][j] = min(dp[i][k] + dp[k][j], dp[i][j]),
其中 i 是起始点,j 是终止点。k是它们经过的中途点。
通过这个公式不断地更新dp[i][j],得到最短路径长。
我们先定义两个矩阵,minpath[i][j],表示的是从 i 到 j 当前得到的最短路,
road[i][j] = k.表示的是从 i 到 j 点要经过的点是 k 然后不断更新road[k][j],
直到k == j。
这个可以适用与有向图和无向图,就看你minpath[i][j] 怎么初始化了,
#include<iostream>
using namespace std;
const int inf = 0x3f3f3ff3;
const int maxn = 110;
int minpath[maxn][maxn],road[maxn][maxn], n, m, s, t;
void init() {
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
if(i ==j) minpath[i][j] = 0, road[i][j] = j;
else minpath[i][j] = inf, road[i][j] = j;
}
void Floyed() {
for(int k = 1; k <= n; k++) {//中间转折点。
for(int i = 1; i <= n; i++) {//起始点。
for(int j = 1; j <= n; j++) {//终点。
if(minpath[i][j] > minpath[i][k] + minpath[k][j]) {//当前的路是否更好,
minpath[i][j] = minpath[i][k] + minpath[k][j];
road[i][j] = road[i][k];
}
}
}
}
for(int i = 1; i <= n; i++) {
t = s;
cout << minpath[s][i] <<endl;//s->t的花费。
while(t != i) {//从起点开始输出路径。
cout << t << "->";
t = road[t][i];//不断更新路径点。
}
cout << i <<endl;
}
}
int main() {
cin >> n >> m >> s;//输入表示n个点,m条边,求s为起始点,求其到 n 个点的距离。
init();//初始化,
int x, y;
for(int i = 0; i < m; i++) {//输入边。
cin >> x >> y;
cin >> minpath[x][y];
}
Floyed();//算法本体,
return 0;
}
最后运行情况,加上了路径的输出。
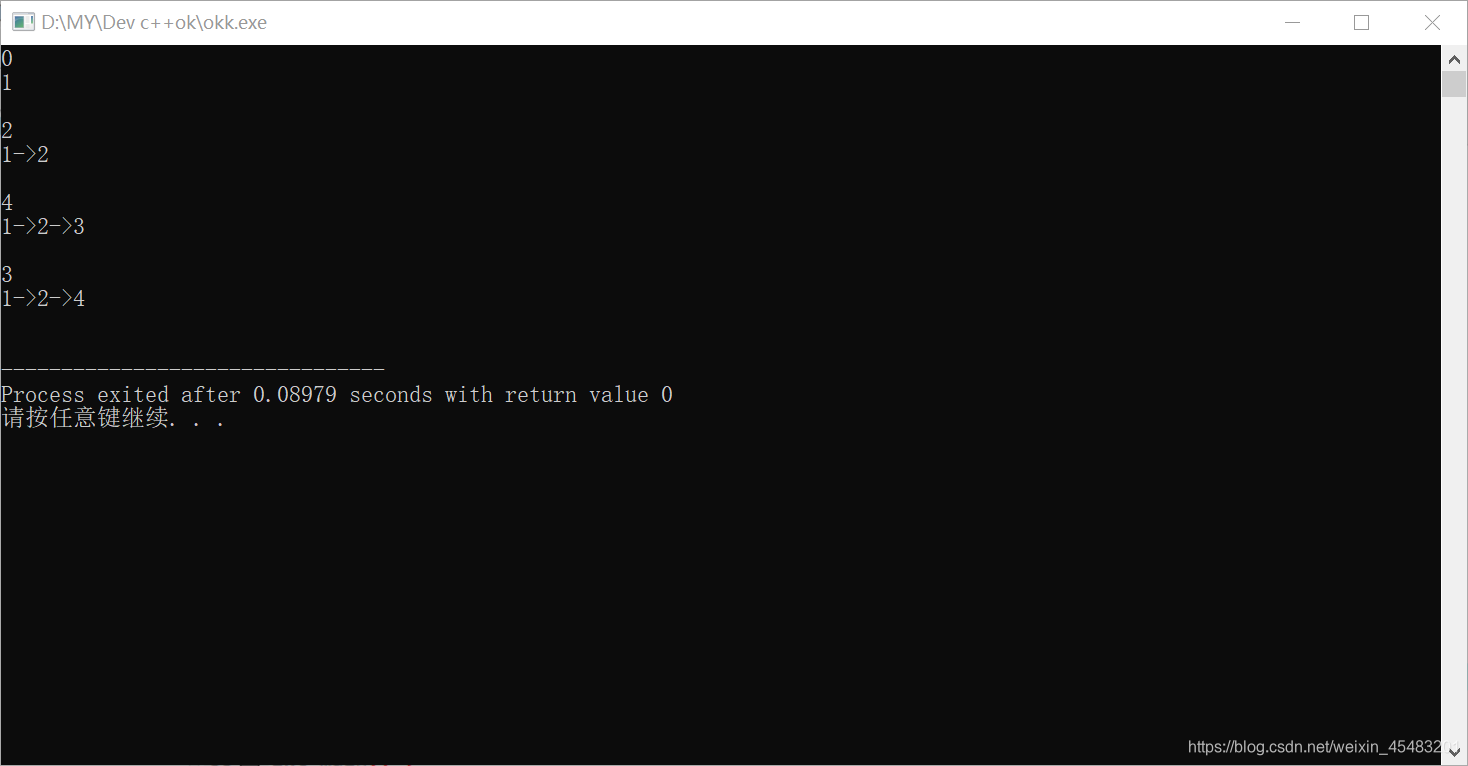
说明一下我上面的代码并不是这道题目的正解,就算上面的代码除去我的路径输出也是错的,
题目的n到了1e4,而这种方法最多就是处理一两百的数据,
这里就是为了方便举个例子。