网络流初步 + Edmond-Karp算法

网络流初步 + Edmond-Karp算法

网络流的基本概念

• 源点，这个点只有流量的流出，没有流入。
• 汇点，这个点只有流量的流入，没有流出。
• 容量，每条有向边的最大可承受的流的理论大小。
• 流量，每条有向边的最大可承受的流的实际大小。
• 最大流，从源点可流入汇点的最大流量。

Edmond-Karp算法

1、如果可以找到增广的路径，取这条路径上的最小的容量作为当前的可增广的流量。

2、在这条增广的路径中的每一个有向边减去当前可增广的流量，同时在其反向边加上当前可增广的流量。

3、重复1的操作，如果不能找到可增广的路径，则说明，已经找到了最大流，输出答案即可。

为什么要在反向边上增加上当前可增广的流量。

毫无疑问这张图的最大流是(4 = 2(1 -> 3 -> 4) + 2(1 -> 2 -> 4))

但是如果我们找寻的一条增广路径是(2(1 -> 2 -> 3 -> 4))之后，我们再也就找不到其他的增广路径了

但是如果我们在每一次取用这条边之后，在其反方向增加对应的反向边。

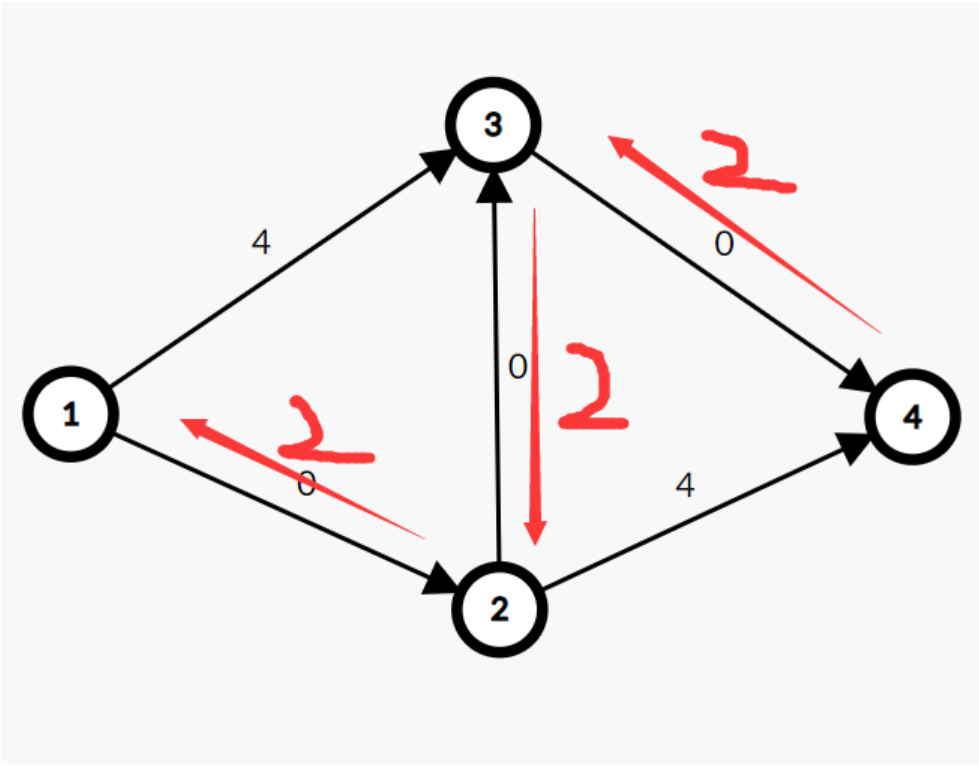
显然我们可以得到另一个增广路径(2(1 -> 3 -> 2 -> 4))，这里我们得到的最大流，也是正确答案。

板子 + 例题

Flow Problem 题目链接

#include <bits/stdc++.h>

using namespace std;

const int INF = 0x3f3f3f3f;

int maze[20][20], n, m;
int visit[20], pre[20];

bool bfs(int st, int ed) {
    queue<int> q;
    memset(visit, 0, sizeof visit);
    q.push(st);
    visit[st] = 1;
    while(!q.empty()) {
        int temp = q.front();
        q.pop();
        if(temp == ed)  return true;
        for(int i = 1; i <= n; i++) {
            if(!visit[i] && maze[temp][i] > 0) {
                visit[i] = 1;
                q.push(i);
                pre[i] = temp;
            }
        }
    }
    return false;
}

int max_flow(int st, int ed) {
    int ans = 0;
    while(bfs(st, ed)) {
        int now_max = INF;
        int p = ed;
        while(p != st) {
            now_max = min(now_max, maze[pre[p]][p]);
            p = pre[p];
        }
        p = ed;
        while(p != st) {
            maze[pre[p]][p] -= now_max;
            maze[p][pre[p]] += now_max;
            p = pre[p];
        }
        ans += now_max;
    }
    // cout << ans << endl;
    return ans;
}

int main() {
    // freopen("in.txt", "r", stdin);
    int t, x, y, w;
    scanf("%d", &t);
    for(int cas = 1; cas <= t; cas++) {
        scanf("%d %d", &n, &m);
        memset(maze, 0, sizeof maze);
        for(int i = 0; i < m; i++) {
            scanf("%d %d %d", &x, &y, &w);
            maze[x][y] += w;
        }
        printf("Case %d: %d
", cas, max_flow(1, n));
    }
    return 0;
}