可持久化线段树又名主席树,是“可持久化”的线段树 (废话)
它能干什么呢? 我们来看这样一道题:【模板】可持久化线段树
题目要求我们支持两种操作,修改历史版本和查询历史版本。
我们可以很轻松地想到一个显然的做法:对每个历史版本开一棵线段树并且储存下来。
OK,这就是可持久化线段树了...
吗?
当然不是,对于每个询问都开一棵SegmentTree,且每棵都要开4倍空间。
那询问次数多一点,空间不就炸了吗?
这就是可持久化线段树高明的地方:我们每次不开一整棵树,而是每次把修改节点插入。
也就是插入一些历史节点来储存历史值。
建出来的可持久化线段树大概长这样,还是理解一下就好( 画图真难用 ):
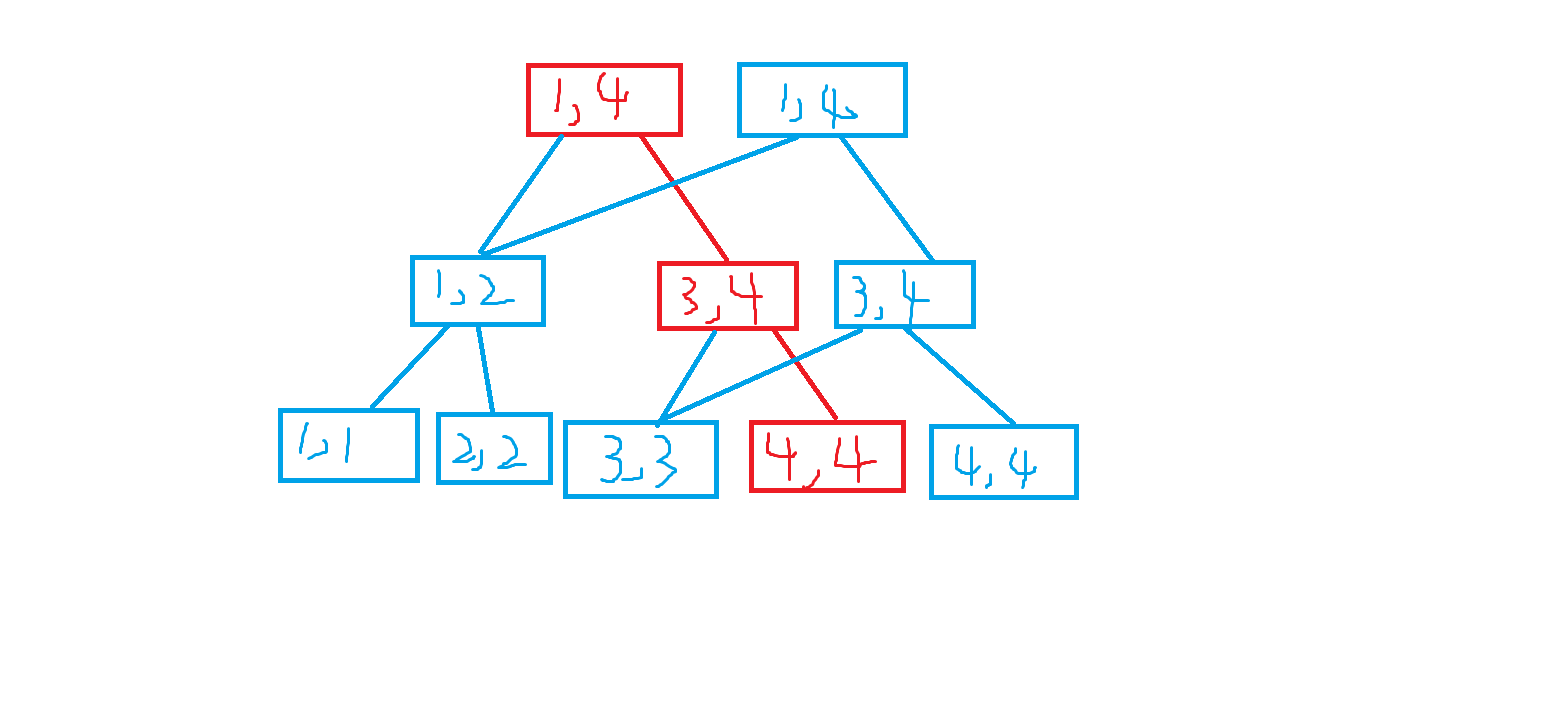
图中的红色节点即为历史节点,它右边多的那些就是新创建的修改节点。
这样我们就可以很方便的查询和修改各个历史版本的值了。
而且,这样做我们的空间复杂度就降到了O(nlogn),高效便捷。
那么我们怎么来构造这一棵PST呢?
首先,跟动态开点线段树一样,我们每个节点保存左右儿子的编号。
然后我们开一个rt[maxn*LOG]的数组来记录每个版本的线段树的根。
可以发现,我们从每个rt开始都是一棵完整的线段树,这样,
我们的查询和访问就可以对应每一个版本的线段树了。
代码我这次会在最后全部放出( 已加好注释,请放心食用 )。
接下来讲修改,
我们每次修改也类似动态开点线段树,先开一个点,然后让新的版本继承老版本。
也就是把你要修改的历史版本的点copy到一个新点上,然后再修改。
这样,我们历史版本的线段树就没有变化,以后还是可以访问这一个版本的线段树。
但是修改操作对应版本的线段树已经建出来了,查询这个版本就可以得到修改后的结果。
那怎么查询呢?
答案是,和动态开点线段树完全一样,直接从你要查询的版本开始递归遍历它的左右子树就ok了。
这里关于修改操作再多说几句,
一般可持久化线段树的题目只要求单点修改,区间修改可以实现不过复杂度比较高。
真的遇到了需要写主席树而且要求区间修改的题目,一般可以转化为单点修改进行操作。
不是i=l...r进行单点修改,而是需要靠思维能力来想到转化的方法。
主席树不难写,考的一般不是怎么写主席树,而是怎么用主席树来解决问题。
所以,灵活运用数据结构,掌握数据结构的思想,才是解决问题的关键。
那本篇博客就讲到这里了,接下来放上面那道例题的标程:
#include<bits/stdc++.h> #define N 1000005 #define LOG 20//开nlogn个节点 using namespace std; inline int read(){ int data=0,w=1;char ch=0; while(ch!='-' && (ch<'0'||ch>'9'))ch=getchar(); if(ch=='-')w=-1,ch=getchar(); while(ch>='0' && ch<='9')data=data*10+ch-'0',ch=getchar(); return data*w; } int a[N],n,m,rt[N*LOG];// struct Persistable_Segment_Tree{ int lc[N*LOG],rc[N*LOG],val[N*LOG],ncnt;//左右子树编号,节点信息,节点个数 inline void build(int &o,int l,int r){ o=++ncnt;//开点 if(l==r){ val[o]=a[l];return;//叶子节点储存信息 } int mid=(l+r)>>1; build(lc[o],l,mid);build(rc[o],mid+1,r);//递归建树 } inline void insert(int &o,int pre,int l,int r,int x,int v){ o=++ncnt;//开点 lc[o]=lc[pre];rc[o]=rc[pre];val[o]=val[pre];//copy历史版本的信息 if(l==r){ val[o]=v;return;//叶子节点储存信息 } int mid=(l+r)>>1; if(x<=mid)insert(lc[o],lc[pre],l,mid,x,v); else insert(rc[o],rc[pre],mid+1,r,x,v);//递归插入 } inline int query(int &o,int l,int r,int x){ if(l==r)return val[o]; int mid=(l+r)>>1; if(x<=mid)return query(lc[o],l,mid,x); else return query(rc[o],mid+1,r,x); } }PST; int main(){ n=read();m=read(); for(int i=1;i<=n;i++)a[i]=read(); PST.build(rt[0],1,n); for(int i=1;i<=m;i++){ int pre=read(),opt=read(),x=read(); if(opt==1){ int v=read(); PST.insert(rt[i],rt[pre],1,n,x,v);//保存修改后的版本 }else if(opt==2){ printf("%d ",PST.query(rt[pre],1,n,x));//查询老版本 rt[i]=rt[pre];//没有修改,直接继承老版本 } } return 0; }
各位如果对博客内容存在疑惑或者不懂的地方欢迎在评论区留下你们的问题和意见。
撰文不易,希望帮到各位。
下一篇讲线段树合并,本系列一直更新,求点赞求关注QuQ。