机器学习_神经网络基础

一、生物神经元与神经网络相关的部分

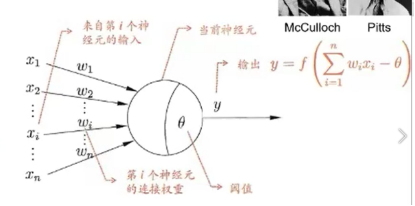
1.每个神经元都是一个多输入单输出的信息处理单元；

2.神经元具有空间整合和时间整合特性；

3.神经元输入分兴奋性输入和抑制性输入两种类型；

4.神经元具有阈值特性。

二、M-P神经元

 

 

三、为什么需要激活函数

从神经元角度：

神经元继续传递信息、产生新连接的概率（超过阈值被激活，但不一定传递）

从数学的角度：

没有激活函数相当于矩阵连乘

1. 多层和一层一样 2.只能拟合线性函数

 

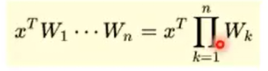
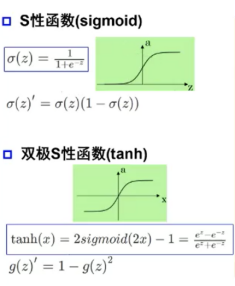
四、常见激活函数举例

 

五、单层感知器

1. M-P神经元的权值预先设置，无法学习
2. 单层感知器是首个可以学习的人工神经网络

 

非线性激活函数

 

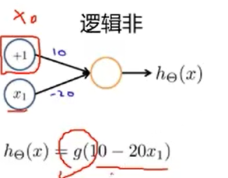
1. 逻辑非的实现

 

 2.逻辑与

 

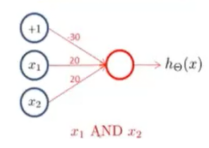
 3.逻辑或

 

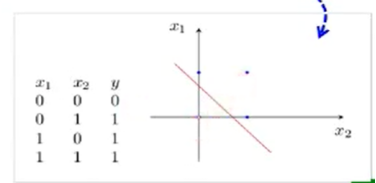
单层感知器能实现一些简单与非或问题，但是非线性问题呢？（如异或）

单层->多层感知器（可以证明单层感知器无法解决异或问题）

可以将异或问题转化为简单的逻辑电路问题，既可以通过多层感知器来解决这个问题。

Eg.用三层感知器实现同或门

 

 

六、万有逼近定理

如果一个隐层包含足够多的神经元，三层前馈神经网络（输入-隐层-输出）能以任意精度逼近任意预定的连续函数。

为什么线性分类任务组合后可以解决非线性分类任务？

可以理解为第一层感知器做的是空间的变化（运用线性代数相关知识）类似于加入变换后的支持向量机。

双隐层感知器逼近非连续函数

当隐层足够宽时，双隐层感知器（输入-隐层1-隐层2-输出）可以逼近任意非连续函数：可以解决任何复杂的分类问题。

 

为何神经网络的层数越多，解决问题的能力越强大？

 

完成输入->输出空间变换

 

神经网络学习如何利用矩阵的线性变换加激活函数的非线性变换，将原始输入空间投影到线性可分的空间去分类/回归。

增加节点数：增加维度，即增加线性转换能力。

增加层数：增加激活函数的次数，即增加非线性转换次数。

七、更宽or更深？

更深更好。

1. 在神经元总数相当的情况下，增加网络深度可以比增加宽度带来更强的网络表示能力：产生更多的线性区域。
2. 深度和宽度对函数复杂度的贡献是不同的，深度的贡献是指数增长的，而宽度的贡献是线性的。

 

 

多层神经网络的问题：梯度消失？

神经网络的参数学习：误差反向传播

 

 

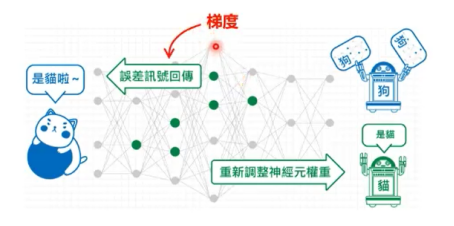
梯度和梯度下降

 

1. 为什么沿着这个方向可以使函数值下降：利用泰勒公式
2. 对于凸函数只有一个极值点，非凸函数非常依赖初始值的选择。

误差反向传播

符合函数的链式求导

 

三层前馈神经网络的BP算法

 

 

 

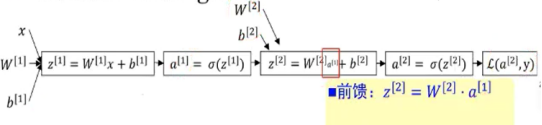
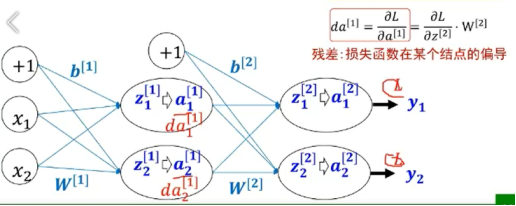
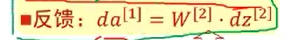
关键理解反向传播名字的来历。

深度学习开发框架（pyTorch）

多层神经网络的问题：梯度消失？

 

 

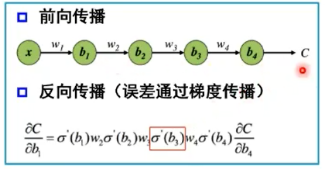
增加深度会导致梯度消失，误差无法传播；

多层网络容易陷入局部极值，难以实现。

故：三层神经网络是主流  预训练、新激活函数使深度成为可能

八、神经网络的“第二次落”

此时的缺点：

1. 训练困难（梯度消失、局部极值）
2. 参数多，计算力不够
3. 数据不够

支持向量机优点：

1. 全局最优解（凸二次规划）
2. 无需调参
3. 基于支持向量，小样本训练

神经网络的“第三次起”

九、逐层预训练

问题一：局部极小值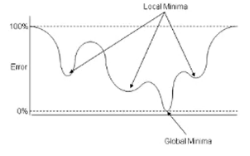

问题二：梯度消失

1. 不同的初始值会收敛到不同的极值点
2. 经过逐层训练后的相对不会那么发散
3. 经过逐层训练它的训练会更快

两种方式实现

受限玻尔兹曼机（RBM）和自编码器

自编码器

 

自编码器假设输入与输出（target = input），是一种尽可能复现输入信号的神经网络。

将input输入一个encoder编码器，就会得到一个code；加一个decoder解码器，输出信息。

通过调整encoder和decoder的参数，是的重构误差最小

没有额外监督信息：无标签数据 误差的来源是直接重构后信号与原输入相比得到

 

自编码器一般是一个多层神经网络（最简单：三层）

训练目标是使输出层与输入层误差最小；

中间隐层是代表输入的特征，可以最大程度上代表原输入信号。

 

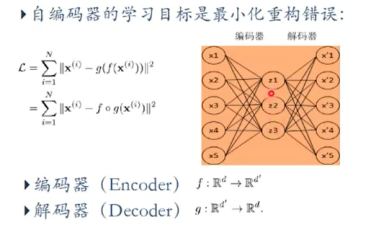
自编码器最初被提出用来降维

堆叠自编码器

1. 将多个自编码器得到的隐层串联；
2. 所有层预训练完成后，进行基于监督学习的全网络微调。

 

受限玻尔兹曼机（RBM）

模型结构

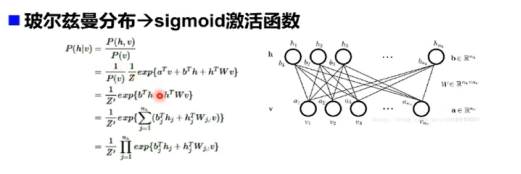
1. RBM是两层神经网络，包含可见层v（输入层）和隐藏层h
2. 不同层之间全连接，层内无连接->二分图
3. 与感知器不同，RBM没有显式的重构过程：

 

1. 目的是让隐藏层得到的可见层与原来的可见层分布一致，从而使隐藏层作为可见层输入的特征。
2. 两个方向权重w共享，偏置不同
3. 模型参数：w, c, b

条件概率建模

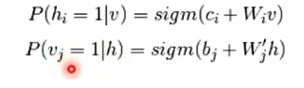
由贝叶斯公式得到条件概率。

 

 

 

 

 

 

 

RBM到DBN（深度信念网络）

一个DBN模型由若干个RBM堆叠而成，最后加一个监督层（BP网络）

训练过程由低到高逐层训练：

1. 最底层RBM以原始输入数据训练
2. 将底部RBM抽取的特征作为顶部RBM的输入继续训练
3. 重复这个过程训练尽可能多的RBM层
4. 基于监督信息通过全局优化算法对网络进行微调，使模型收敛

DBN和DBM的区别

1. DBM没有监督层，是若干个RBM的直接堆叠
2. 无向图模型，每两层间互有反馈。

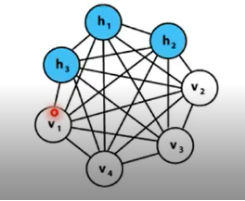
一般玻尔兹曼机（BM）

可见层和隐藏内部节点之间可连接

具有很强大的无监督学习能力能够学习数据中复杂的规则

随机神经网络和递归神经网络的一种

 

全连接图，复杂度很高

1. 难以准确计算BM所表示的分布
2. 难以抽样得到服从BM所表示分布的随机样本

 

 

自编码机和受限玻尔兹曼机的区别

结构上：

自编码器编码和解码函数不同：W1，W2

RBM共享权重矩阵W，两个偏置向量

原理上：

自编码器通过非线性变换学习特征，是确定的，特征值可以为任何实数

RBM基于概率分布定义，高层表示为底层特征的条件概率，输出只有两种状态（未激活激活），用二进制0/1表示；

训练优化：

自编码器通过最损失函数L最小化重构输入数据，直接用BP优化求解

RBM基于最大似然，能量函数偏导无法直接计算，基于采样方法进行估计

生成/判别模型：

RBM对联合概率密度建模，是生成式模型；

自编码器直接对条件概率建模，是判别式模型

 

ReLU更好

解决梯度消失问题的方法

 

波尔兹曼机的理论和应用意义

BM和RBM数学上很漂亮，且有统计物理学支撑；

但受结构限制严重，生成式模型效果往往不如判别式模型；

主流的深度学习平台甚至都不支持RBM和预训练

理论：

1. 模型结构：网络拓扑结构优化
2. 学习算法：非线性优化过程近似

 

应用：

作为一种概率生成式模型应用到了协同滤波推荐、数据降维、时间序列降维问题。

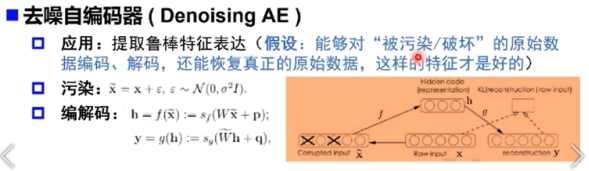
自编码器变种

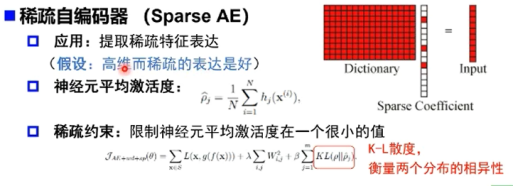
正则自编码器（Regularized AE）

 

 

 

两个问题

问题1：深层网络的局部极小值是非凸的激活函数导致的么？如果是，为什么不用凸激活函数？

1. 深层网络的局部极小值主要是多个隐层符合导致的；
2. ReLU就是凸激活函数，但多个凸激活函数的符合也不一定是凸的：比如f(x) = exp(-x)
3. 在x>0时凸的，但f(f(x))就是非凸的

 

问题2：逐层预训练真的是为了找到更阿红的局部极小值么？

深度网络参数太多，梯度下降在非常高维空间进行，很难得到在所有维度上都是局部最小的局部最小值；

大多数情况参数落在了鞍点处：某些维度上时最低点，某些维度上是最高点->增加扰动很容易跳出鞍点。