[C++]各种排序算法合集（冒泡，选择，插入，shell，基数，快排，归并）

#pragma once
#ifndef SORT_COLLECTIONS_H_
#define SORT_COLLECTIONS_H_
#include <assert.h>
#include <algorithm>
#include <stdlib.h>
#include <time.h>
//#include "generic.h"
using namespace std;
namespace alg {
    //1：冒泡排序，时间复杂度为O(n^2)，稳定，一种传统的排序方法，核心思想是通过不断的遍历整个数组交换顺序达到排序目的。
    template<typename T>
    static void BubbleSort(T list[], int start, int end) {
        int i;
        bool swapped;
        assert(start < end);
        do {
            swapped = false;
            for (int i = start + 1; i <= end; ++i) {
                if (list[i - 1] > list[i]) {
                    swap(list[i - 1], list[i]);
                    swapped = true;
                }
            }
            end--;
        } while (swapped);
    }
    //选择排序，时间复杂度为O(n^2)，不稳定，从前到后，第一层循环所在的索引与其后面的值进行比较选择出最小的并进行交换，优点是不占用额外内存
    template <typename T>
    static void SelectionSort(T list[], int start, int end) {
        int i, j;
        int iMin;
        assert(start < end);
        for (j = start; j < end; ++j) {
            iMin = j;
            for (i = j + 1; i <= end; ++i) {
                if (list[i] < list[iMin]) {
                    iMin = i;
                }
            }
            if (j != iMin)
                swap(list[j], list[iMin]);
        }
    }
    //插入排序，时间复杂度为O(n^2)，稳定，第一层循环遍历后的所有元素都是已序的，第一层循环遍历到的每一个元素都会与前面已序元素进行比较，直到比已序的某个元素大时停止比较并插入其前面
    template<typename T>
    static void InsertionSort(T list[], int num_of_elems) {
        int i, j;
        for (i = 1; i < num_of_elems; ++i) {
            T current_elem = list[i];
            j = i - 1;
            while (j>=0&&list[j]>current_elem)
            {
                list[j + 1] = list[j];
                j--;
            }
            list[j + 1] = current_elem;
        }
    }
    //希尔排序，也叫递减增量排序算法，时间复杂度O(n^(1.3—2))，不稳定，选取合适的递减增量值，对不同增量下的子数组进行插入排序。
    template<typename T>
    static void ShellSort(T list[], int len) {
        int h = 1;
        int i, j;
        while (h < len / 3)
        {
            h = h * 3 + 1;
        }
        while (h>=1)
        {
            for (i = h; i < len; ++i) {
                T current_elem = list[i];
                j = i - h;
                while (j >= 0&&current_elem<list[j])
                {
                    list[j + h] = list[j];
                    j = j - h;
                }
                list[j + h] = current_elem;
            }
            h /= 3;
        }
    }
    //基数排序，时间复杂度O(d(n+rd))，稳定，其原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。由于整数也可以表达字符串（比如名字或日期）和特定格式的浮点数，所以基数排序也不是只能使用于整数。
    //for radix_sort,find the biggest number of list
    template <typename T>
    static int maxbit(T list[], int n) {
        int maxData = list[0];
        for (int i = 1; i < n; ++i) {
            if (maxData < list[i])
                maxData = list[i];
        }
        int d = 1;
        int p = 10;
        while (maxData >= p)
        {
            maxData /= 10;
            d++;
        }
        return d;
    }
    template <typename T>
    static void RadixSort(T list[], int n) {
        int d = maxbit(list, n);
        int *temp = new T[n];
        int *count = new int[10];
        int i, j, k;
        int radix = 1;
        for (i = 0; i < d; ++i) {
            for (j = 0; j < 10; ++j)
                count[j] = 0;
            for (j = 0; j < n; ++j) {
                k = (list[j] / radix) % 10;
                count[k]++;
            }
            for (j = 1; j < 10; ++j)
                count[j] += count[j - 1];
            for (j = n - 1; j >= 0; --j) {
                k = (list[j] / radix) % 10;
                temp[count[k] - 1] = list[j];
                count[k]--;
            }
            for (j = 0; j < n; ++j)
                list[j] = temp[j];
            radix *= 10;
        }
        delete[] temp;
        delete[] count;
    }
    //快速排序，时间复杂度O(nlogn)，不稳定，主要思想是选择基准哨兵，将原数组分为两部分进行，一边是都不大于基准的部分，一边是都大于基准的部分，按此法递归，直至整个数组有序。
    template<typename T>
    static int partition(T list[], int begin, int end) {
        srand(time(0));
        //int pivot_indx = RANDOM(begin, end);
        int pivot_indx = begin + rand() % (end - begin + 1);
        T pivot = list[pivot_indx];
        swap(list[begin], list[pivot_indx]);
        int i = begin + 1;
        int j = end;
        while (i <= j)
        {
            while (i <= end && (list[i] <= pivot))
                ++i;
            while (j >= begin && (list[j] > pivot))
                --j;
            if (i < j)
                swap(list[i], list[j]);
        }
        swap(list[begin], list[j]);
        return j;
    }
    template<typename T>
    static void QuickSort(T list[], int begin, int end) {
        if (begin < end) {
            int pivot_indx=partition<T>(list, begin, end);
            QuickSort(list, begin, pivot_indx - 1);
            QuickSort(list, pivot_indx + 1, end);
        }
    }
    //归并排序，时间复杂度O(nlogn)，稳定，将数组不断切分至单个元素，然后进行排序，将排序后的子数组再作为已序数组供上层进行选择排序。
    template<typename T>
    static void merge_(T *list, int l, int m, int h) {
        T *A = list + l;
        int lb = m - l;
        T *B = new T[lb+1];
        for (int i = 0; i <= lb; B[i] = A[i++]);
        int lc = h - (m + 1);
        T *C = list + m + 1;
        for (int i = 0, j = 0, k = 0; (j <= lb) || (k <= lc);) {
            if ((j <= lb) && (!(k <= lc) || (B[j] <= C[k])))
                A[i++] = B[j++];
            if ((k <= lc) && (!(j <= lb) || (C[k] < B[j])))
                A[i++] = C[k++];

        }
        delete[] B;
    }
    template<typename T>
    static void MergeSort(T *list, int l, int h) {
        if (h - l < 1) return;
        int m = (l + h) >> 1;
        MergeSort(list, l, m);
        MergeSort(list, m+1, h);
        merge_(list,l, m, h);
    }
}
#endif // !SORT_COLLECTIONS_H_

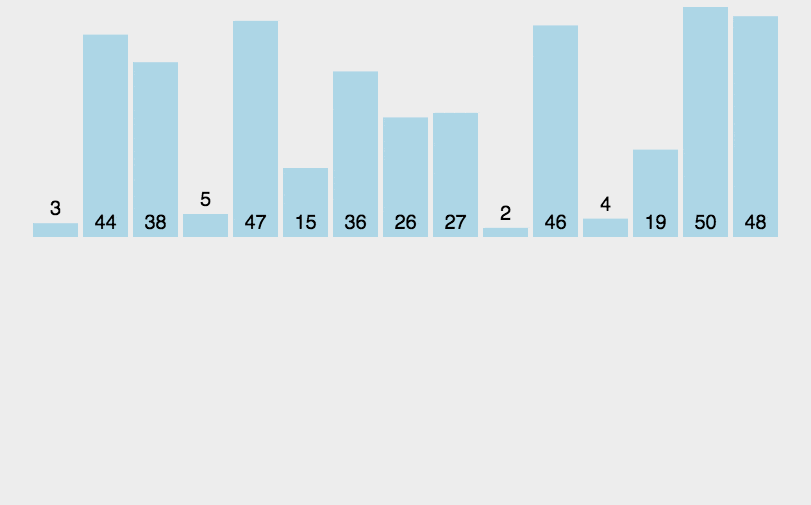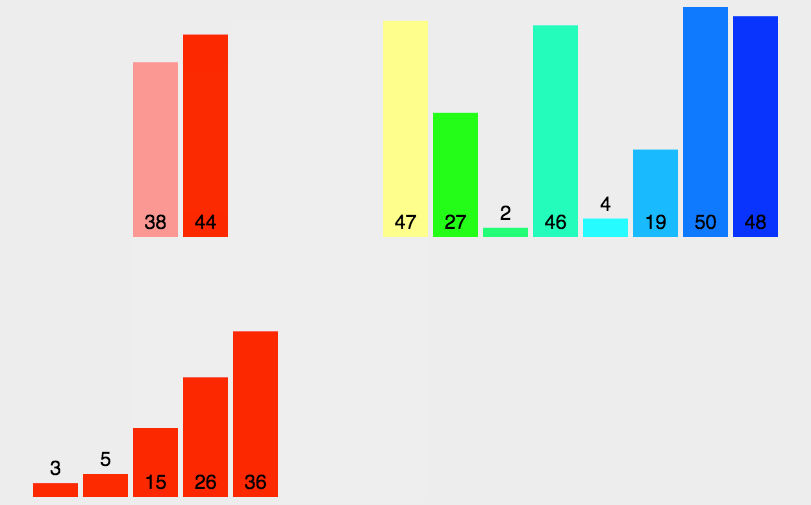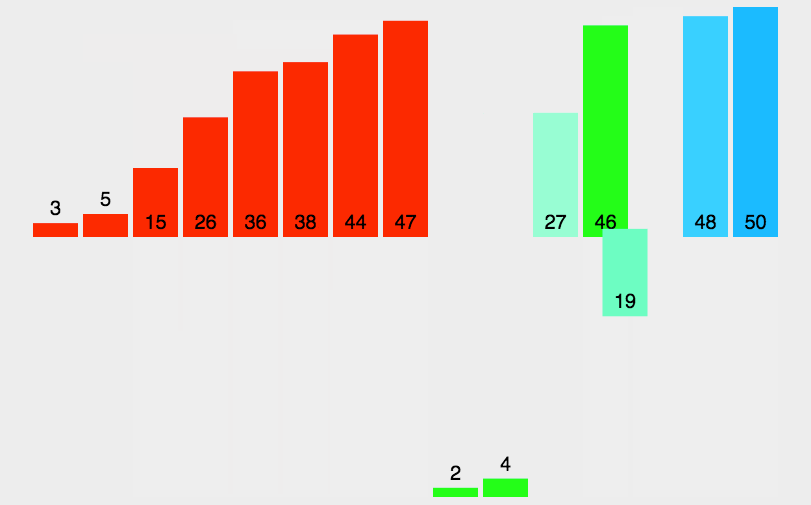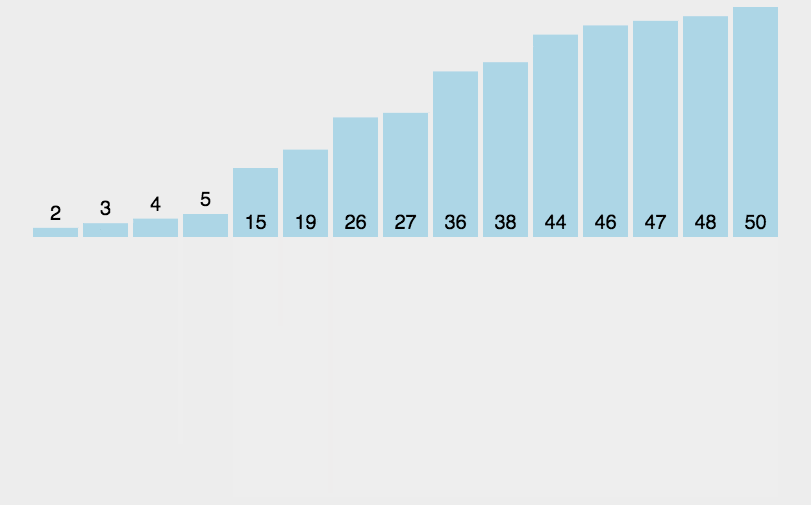
 排序算法的动图演示

冒泡排序

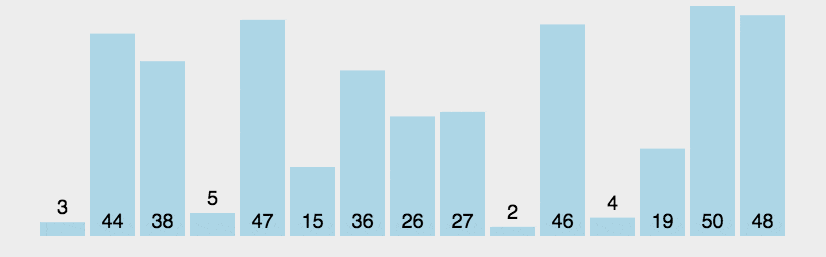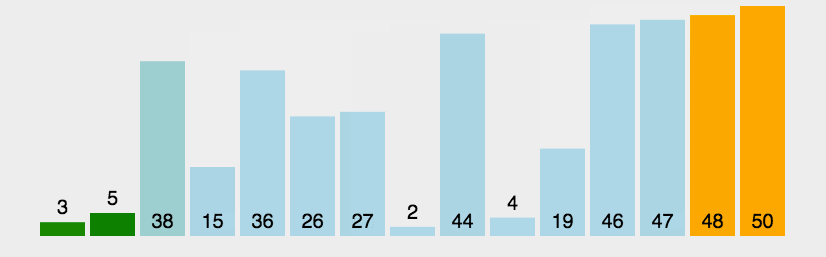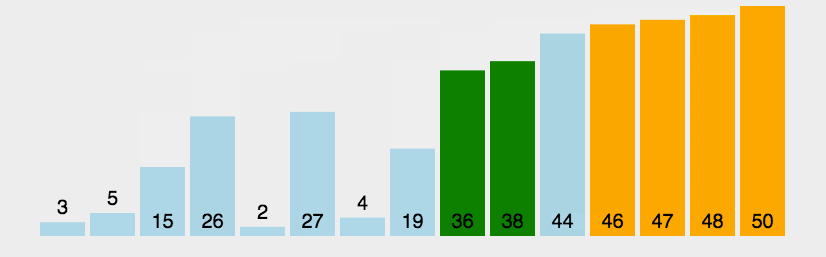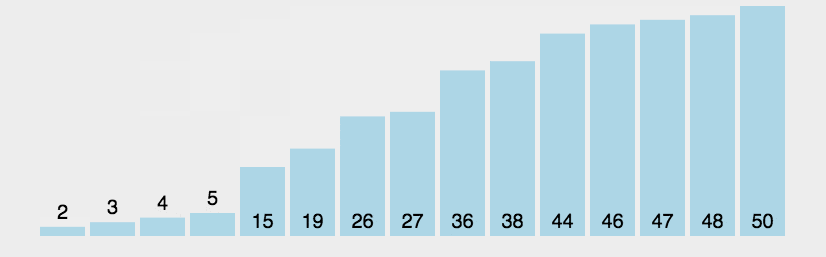
选择排序

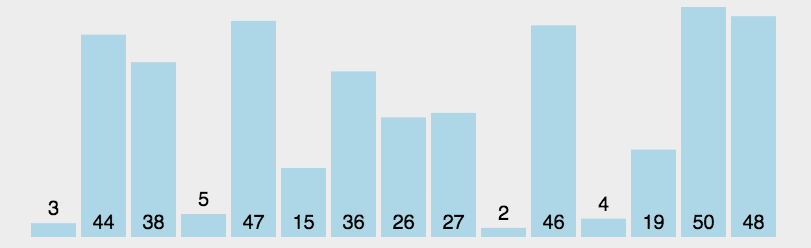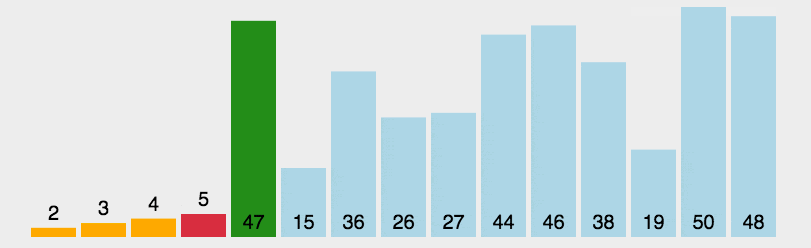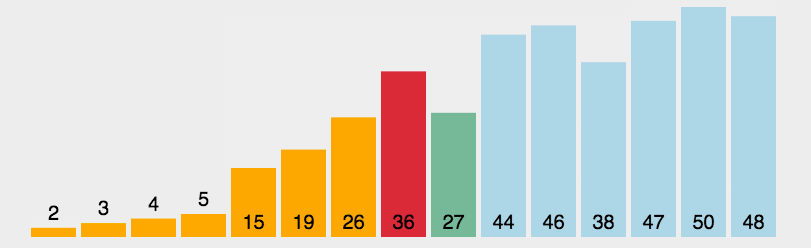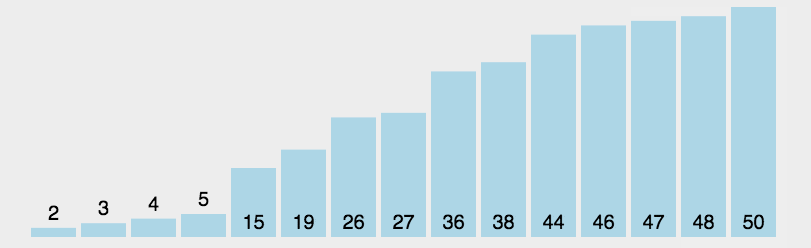
插入排序

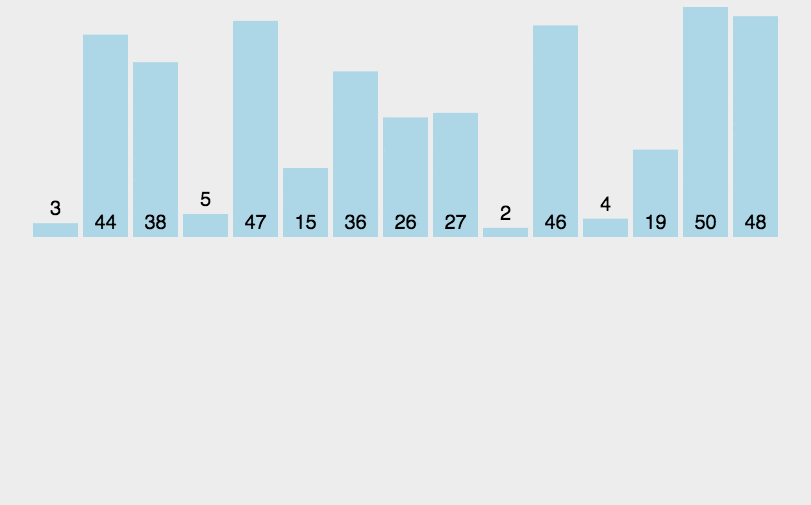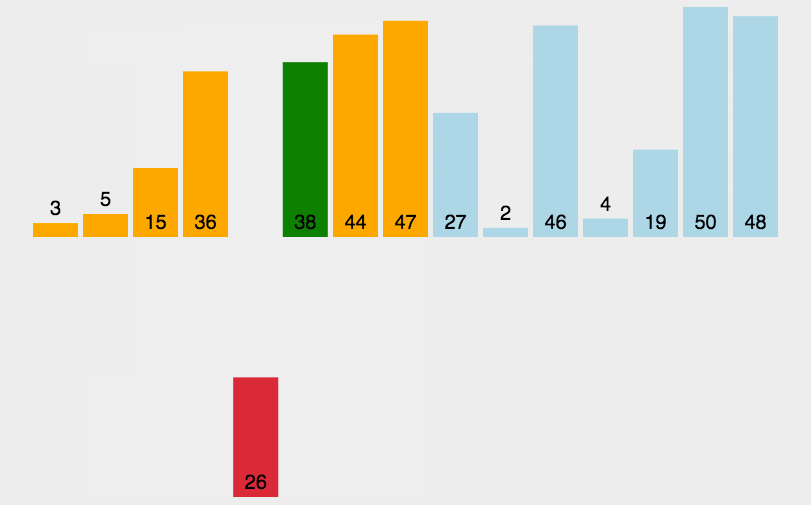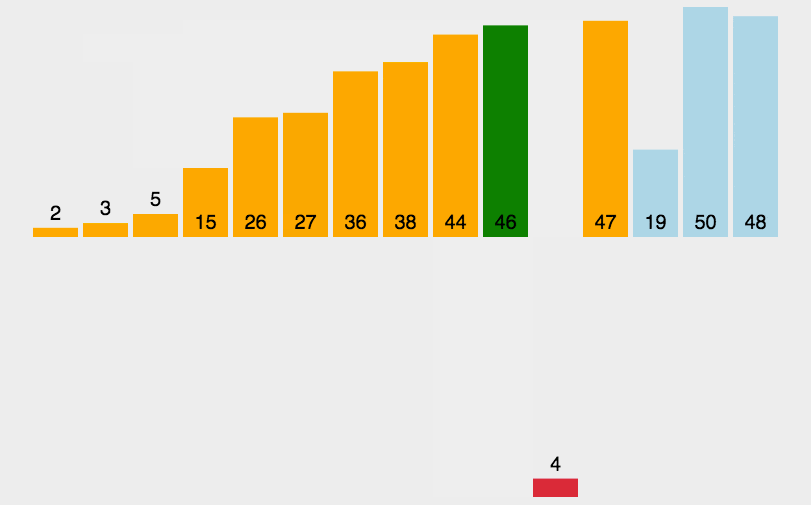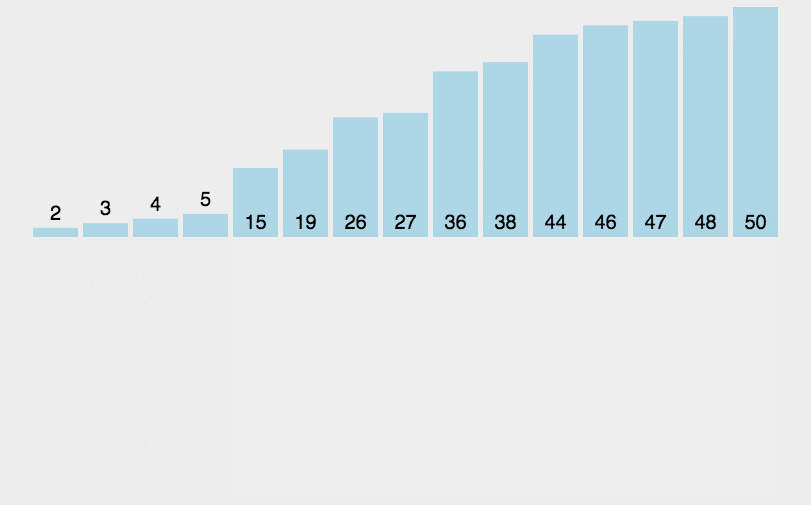
希尔排序

基数排序

归并排序

图片转自--https://www.runoob.com/w3cnote_genre/algorithm