POJ 1003：Hangover

Hangover

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 109231		Accepted: 53249

Description

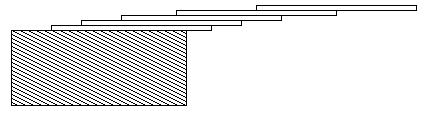
How far can you make a stack of cards overhang a table? If you have one card, you can create a maximum overhang of half a card length. (We're assuming that the cards must be perpendicular to the table.) With two cards you can make the top card overhang the bottom one by half a card length, and the bottom one overhang the table by a third of a card length, for a total maximum overhang of 1/2 + 1/3 = 5/6 card lengths. In general you can make n cards overhang by 1/2 + 1/3 + 1/4 + ... + 1/(n + 1) card lengths, where the top card overhangs the second by 1/2, the second overhangs tha third by 1/3, the third overhangs the fourth by 1/4, etc., and the bottom card overhangs the table by 1/(n + 1). This is illustrated in the figure below.

Input

The input consists of one or more test cases, followed by a line containing the number 0.00 that signals the end of the input. Each test case is a single line containing a positive floating-point number c whose value is at least 0.01 and at most 5.20; c will contain exactly three digits.

Output

For each test case, output the minimum number of cards necessary to achieve an overhang of at least c card lengths. Use the exact output format shown in the examples.

Sample Input

1.00
3.71
0.04
5.19
0.00

Sample Output

3 card(s)
61 card(s)
1 card(s)
273 card(s)

水题，求 1/2 + 1/3 + 1/4 + ... + 1/(n + 1)>=c的最小n。输出时候注意要将退出的n减2才符合条件。

代码：

#include <iostream>
using namespace std;

int main()
{
	double x,sum=0;
	int n;
	cin>>x;
	for(;;)
	{
		if(!x)
		 break;
		for(n=2;;n++)
		{
			if(sum>x)
				break;
			sum=sum+(double)1/n;
		}
		cout<<n-2<<" card(s)"<<endl;
		sum=0;
		cin>>x;
	}
	return 0;
}

版权声明：本文为博主原创文章，未经博主允许不得转载。