| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 7561 | Accepted: 2194 |
Description
RJ Freight, a Japanese railroad company for freight operations has recently constructed exchange lines at Hazawa, Yokohama. The layout of the lines is shown in Figure 1.
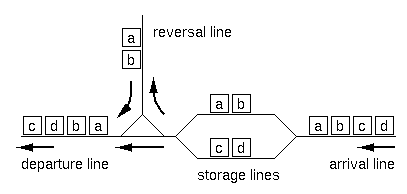
Figure 1: Layout of the exchange lines
A freight train consists of 2 to 72 freight cars. There are 26 types of freight cars, which are denoted by 26 lowercase letters from "a" to "z". The cars of the same type are indistinguishable from each other, and each car's direction doesn't matter either. Thus, a string of lowercase letters of length 2 to 72 is sufficient to completely express the configuration of a train.
Upon arrival at the exchange lines, a train is divided into two sub-trains at an arbitrary position (prior to entering the storage lines). Each of the sub-trains may have its direction reversed (using the reversal line). Finally, the two sub-trains are connected in either order to form the final configuration. Note that the reversal operation is optional for each of the sub-trains.
For example, if the arrival configuration is "abcd", the train is split into two sub-trains of either 3:1, 2:2 or 1:3 cars. For each of the splitting, possible final configurations are as follows ("+" indicates final concatenation position):
[3:1]
abc+d cba+d d+abc d+cba
[2:2]
ab+cd ab+dc ba+cd ba+dc cd+ab cd+ba dc+ab dc+ba
[1:3]
a+bcd a+dcb bcd+a dcb+a
Excluding duplicates, 12 distinct configurations are possible.
Given an arrival configuration, answer the number of distinct configurations which can be constructed using the exchange lines described above.
Input
The entire input looks like the following.
the number of datasets = m
1st dataset
2nd dataset
...
m-th dataset
Each dataset represents an arriving train, and is a string of 2 to 72 lowercase letters in an input line.
Output
For each dataset, output the number of possible train configurations in a line. No other characters should appear in the output.
Sample Input
4 aa abba abcd abcde
Sample Output
1 6 12 18
一串字符串,从中间的某一处切开,前后都可能reverse,然后这两部分前后都有可能,即正常情况下可能出现8中不同的字符串。然后问所有这些可能的字符串中有多少种不同的。
自己写hash会TLE,只能自己写。各种麻烦,函数返回局部变量的指针容易出问题,这样不行。
代码:
#include <iostream>
#include <algorithm>
#include <cmath>
#include <vector>
#include <string>
#include <cstring>
#pragma warning(disable:4996)
using namespace std;
#define maxn 80
int num;
//char *wang_reverse,*sub1,*sub2,*sub3,*sub4;
//char *res1,*res2,*res3,*res4,*res5,*res6,*res7,*res8;
char sub1[80],sub2[80],sub3[80],sub4[80];
char res1[80],res2[80],res3[80],res4[80],res5[80],res6[80],res7[80],res8[80];
struct no
{
char str[maxn];
}node[maxn*maxn];
void reverse2(char *str)
{
int i,j,len;
len=strlen(str);
for(i=len-1,j=0;i>=0;i--,j++)
sub3[j]=str[i];
sub3[j]='�';
}
void reverse3(char *str)
{
int i,j,len;
len=strlen(str);
for(i=len-1,j=0;i>=0;i--,j++)
sub4[j]=str[i];
sub4[j]='�';
}
void substr(char *str,int i)
{
int j;
for(j=0;j<i;j++)
sub1[j]=str[j];
sub1[j]='�';
}
void substr_rever(char *str,int i)
{
int x,j,len;
len=strlen(str);
for(j=len-1,x=0;j>=i;j--,x++)
sub2[x]=str[j];
sub2[x]='�';
}
void add_str1(char *re1,char *re2)
{
int len1=strlen(re1);
int len2=strlen(re2);
int i,j;
for(i=0;i<len1;i++)
{
res1[i]=re1[i];
}
for(j=0;j<len2;j++)
{
res1[i]=re2[j];
i++;
}
}
void add_str2(char *re1,char *re2)
{
int len1=strlen(re1);
int len2=strlen(re2);
int i,j;
for(i=0;i<len1;i++)
{
res2[i]=re1[i];
}
for(j=0;j<len2;j++)
{
res2[i]=re2[j];
i++;
}
}
void add_str3(char *re1,char *re2)
{
int len1=strlen(re1);
int len2=strlen(re2);
int i,j;
for(i=0;i<len1;i++)
{
res3[i]=re1[i];
}
for(j=0;j<len2;j++)
{
res3[i]=re2[j];
i++;
}
}
void add_str4(char *re1,char *re2)
{
int len1=strlen(re1);
int len2=strlen(re2);
int i,j;
for(i=0;i<len1;i++)
{
res4[i]=re1[i];
}
for(j=0;j<len2;j++)
{
res4[i]=re2[j];
i++;
}
}
void add_str5(char *re1,char *re2)
{
int len1=strlen(re1);
int len2=strlen(re2);
int i,j;
for(i=0;i<len1;i++)
{
res5[i]=re1[i];
}
for(j=0;j<len2;j++)
{
res5[i]=re2[j];
i++;
}
}
void add_str6(char *re1,char *re2)
{
int len1=strlen(re1);
int len2=strlen(re2);
int i,j;
for(i=0;i<len1;i++)
{
res6[i]=re1[i];
}
for(j=0;j<len2;j++)
{
res6[i]=re2[j];
i++;
}
}
void add_str7(char *re1,char *re2)
{
int len1=strlen(re1);
int len2=strlen(re2);
int i,j;
for(i=0;i<len1;i++)
{
res7[i]=re1[i];
}
for(j=0;j<len2;j++)
{
res7[i]=re2[j];
i++;
}
}
void add_str8(char *re1,char *re2)
{
int len1=strlen(re1);
int len2=strlen(re2);
int i,j;
for(i=0;i<len1;i++)
{
res8[i]=re1[i];
}
for(j=0;j<len2;j++)
{
res8[i]=re2[j];
i++;
}
}
bool judge(char *str)
{
int i;
for(i=0;i<num;i++)
{
if(strcmp(str,node[i].str)==0)
{
return false;
}
}
return true;
}
int main()
{
//freopen("i.txt","r",stdin);
//freopen("o.txt","w",stdout);
char wang[80];
int test,i,len;
scanf("%d",&test);
while(test--)
{
for(i=0;i<80;i++)
{
wang[i]='�';
sub1[i]='�';
sub2[i]='�';
sub3[i]='�';
sub4[i]='�';
res1[i]='�';
res2[i]='�';
res3[i]='�';
res4[i]='�';
res5[i]='�';
res6[i]='�';
res7[i]='�';
res8[i]='�';
}
scanf("%s",wang);
num=0;
len=strlen(wang);
for(i=1;i <= len-1;i++)
{
substr(wang,i);//sub1
substr_rever(wang,i);//sub2
reverse2(sub1);//sub3
reverse3(sub2);//sub4
add_str1(sub1,sub2);
add_str2(sub2,sub1);
add_str3(sub3,sub2);
add_str4(sub2,sub3);
add_str5(sub1,sub4);
add_str6(sub4,sub1);
add_str7(sub3,sub4);
add_str8(sub4,sub3);
if(judge(res1))
{
strcpy(node[num].str,res1);
num++;
}
if(judge(res2))
{
strcpy(node[num].str,res2);
num++;
}
if(judge(res3))
{
strcpy(node[num].str,res3);
num++;
}
if(judge(res4))
{
strcpy(node[num].str,res4);
num++;
}
if(judge(res5))
{
strcpy(node[num].str,res5);
num++;
}
if(judge(res6))
{
strcpy(node[num].str,res6);
num++;
}
if(judge(res7))
{
strcpy(node[num].str,res7);
num++;
}
if(judge(res8))
{
strcpy(node[num].str,res8);
num++;
}
}
printf("%d
",num);
}
//system("pause");
return 0;
}版权声明:本文为博主原创文章,未经博主允许不得转载。