Codeforces 601A：The Two Routes 宽搜最短路径

A. The Two Routes

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

In Absurdistan, there are n towns (numbered 1 through n) and m bidirectional railways. There is also an absurdly simple road network — for each pair of different towns x and y, there is a bidirectional road between towns x and y if and only if there is no railway between them. Travelling to a different town using one railway or one road always takes exactly one hour.

A train and a bus leave town 1 at the same time. They both have the same destination, town n, and don't make any stops on the way (but they can wait in town n). The train can move only along railways and the bus can move only along roads.

You've been asked to plan out routes for the vehicles; each route can use any road/railway multiple times. One of the most important aspects to consider is safety — in order to avoid accidents at railway crossings, the train and the bus must not arrive at the same town (except town n) simultaneously.

Under these constraints, what is the minimum number of hours needed for both vehicles to reach town n (the maximum of arrival times of the bus and the train)? Note, that bus and train are not required to arrive to the town n at the same moment of time, but are allowed to do so.

Input

The first line of the input contains two integers n and m (2 ≤ n ≤ 400, 0 ≤ m ≤ n(n - 1) / 2) — the number of towns and the number of railways respectively.

Each of the next m lines contains two integers u and v, denoting a railway between towns u and v (1 ≤ u, v ≤ n, u ≠ v).

You may assume that there is at most one railway connecting any two towns.

Output

Output one integer — the smallest possible time of the later vehicle's arrival in town n. If it's impossible for at least one of the vehicles to reach town n, output  - 1.

Sample test(s)

input

4 2
1 3
3 4

output

2

input

4 6
1 2
1 3
1 4
2 3
2 4
3 4

output

-1

input

5 5
4 2
3 5
4 5
5 1
1 2

output

3

Note

In the first sample, the train can take the route 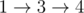 and the bus can take the route . Note that they can arrive at town 4 at the same time.

In the second sample, Absurdistan is ruled by railwaymen. There are no roads, so there's no way for the bus to reach town 4.

题意是有n个点，m条火车道，每一条火车道连接着两个点，没有火车道的边 有客车路，问火车与客车同时从1点出发，两者最终到达n点时，时间最长的那个的最小值。

我算是见识了codeforces水题 唬人的功力了。。。

比赛的时候太困了。。。。搞完AB就一直想睡觉，读了一遍C之后发现要求除了终点之外每个点火车与客车到达时间不能相等。心想这怎么搞，怎么C题就这么难了，睡觉吧。。。。

醒来发现，麻蛋全是骗人的。。。。。

这是一个完全图啊啊啊，点1到n必有路径的啊，也就是说火车与客车 两者到达时间的最小值一定是1，就求剩下的那个的最小值，就是答案了。。。。

对自己写代码能力也真是很伤心。。。

参考代码：

#pragma warning(disable:4996)  
#include <iostream>  
#include <algorithm>  
#include <cmath>  
#include <vector>  
#include <string>  
#include <cstring> 
#include <queue>
using namespace std;

const int maxn = 405;

int n, m;
int dis[maxn];
int connect[maxn][maxn];

int bfs(int val)
{
	queue<int>q;
	memset(dis, -1, sizeof(dis));
	dis[1] = 0;
	q.push(1);

	while (!q.empty())
	{
		int x = q.front();
		q.pop();

		for (int i = 1; i <= n; i++)
		{
			if (connect[x][i] == val&&dis[i] == -1)
			{
				dis[i] = dis[x] + 1;
				q.push(i);
			}
		}
	}
	return dis[n];
}

int main()
{
	//freopen("i.txt", "r", stdin);
	//freopen("o.txt", "w", stdout);
	scanf("%d%d", &n, &m);
	int tx, ty;
	
	for (int i = 0; i < m; i++)
	{
		scanf("%d%d", &tx, &ty);
		connect[tx][ty] = connect[ty][tx] = 1;
	}
	printf("%d
",bfs(1 - connect[1][n]));
	//system("pause");
	return 0;
}