The Embarrassed Cryptographer POJ

The Embarrassed Cryptographer

The young and very promising cryptographer Odd Even has implemented the security module of a large system with thousands of users, which is now in use in his company. The cryptographic keys are created from the product of two primes, and are believed to be secure because there is no known method for factoring such a product effectively.
What Odd Even did not think of, was that both factors in a key should be large, not just their product. It is now possible that some of the users of the system have weak keys. In a desperate attempt not to be fired, Odd Even secretly goes through all the users keys, to check if they are strong enough. He uses his very poweful Atari, and is especially careful when checking his boss' key.

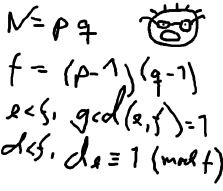
Input

The input consists of no more than 20 test cases. Each test case is a line with the integers 4 <= K <= 10¹⁰⁰ and 2 <= L <= 10⁶. K is the key itself, a product of two primes. L is the wanted minimum size of the factors in the key. The input set is terminated by a case where K = 0 and L = 0.

Output

For each number K, if one of its factors are strictly less than the required L, your program should output "BAD p", where p is the smallest factor in K. Otherwise, it should output "GOOD". Cases should be separated by a line-break.

Sample Input

143 10
143 20
667 20
667 30
2573 30
2573 40
0 0

Sample Output

GOOD
BAD 11
GOOD
BAD 23
GOOD
BAD 31



题意：给出一个由两个素数相乘得到的数字 K 和一个数字 L 要求 K 的较小的那个素数因子 <L 时输出 BAD 否则输出 GOOD。
思路：
素数打表后 从小到大遍历找出能被 K 整除的最小素数判断与 L 的大小关系。
由于 K 很大需要用字符串模拟除法取余操作，但是以十进制方式一位一位取的话会TLE，所以转为千进制，一次取3位模拟取模操作。

代码：

#include <set>
#include <map>
#include <list>
#include <stack>
#include <queue>
#include <deque>
#include <cmath>
#include <string>
#include <vector>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <sstream>
#include <iostream>
#include <algorithm>
//#include <unordered_map>
#define INF 0x3f3f3f3f
#define ll long long
#define ull unsigned long long
#define fcio ios::sync_with_stdio(false); cin.tie(0); cout.tie(0)
using namespace std;
const int maxn=1e6+100;
int prime[maxn];
bool isprime[maxn];
int cnt=0;
void dbprime()
{
    memset(isprime,true,sizeof(isprime));
    isprime[0] = isprime[1] = false;
    for(int i=2;i<maxn;i++)
    {
        if(isprime[i])
        {
            prime[cnt++]=i;
            for(int j=i+i;j<maxn;j+=i)
            {
                isprime[j]=false;
            }
        }
    }
}

int main()
{
    string k;
    dbprime();
    int l;
    while(cin>>k>>l)
    {
        if(k=="0"&&l==0) break;
        bool flag=true;
        for(int i=0;i<cnt&&prime[i]<l;i++)
        {
            int t=0;
            for(int j=0;j<k.size();j+=3)
            {
                int t1=0;
                int pow=1;
                for(int p=j;p<j+3&&p<k.size();p++)
                {
                    pow*=10;
                    t1=t1*10+k[p]-'0';
                }
                t*=pow;
                t+=t1;
                t%=prime[i];
            }
            if(t==0)
            {
                cout<<"BAD "<<prime[i]<<endl;
                flag=false;
                break;
            }
        }
        if(flag) cout<<"GOOD"<<endl;
    }
}