数字三角形问题是一个很经典的dp问题,因为这个题是在书上看到的,所以根本不知道输入是什么!只能通过经验判断输入!!!!
注意:当前版本是我自己臆想出来的输入。
题目描述
有一个非负整数组成的三角形,第一行只有一个数,除了最下行之外每个数的左下方和右下方各有一个数,从第一行的数开始每次可以往左下或者右下走一格,直到走到最下行,把沿途经过的数全部加起来,如何走才能得到最大和?
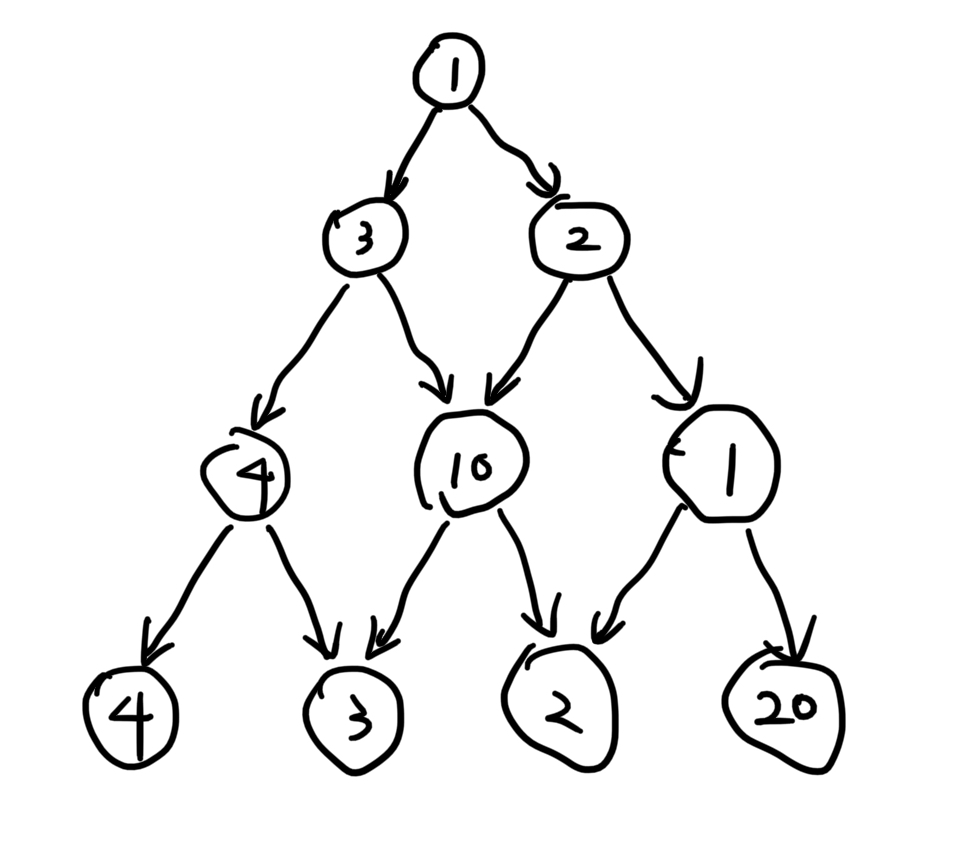
思考过程1
像题目中这样说,不就是转换成一个数组么?
如图所示,先转成数组:
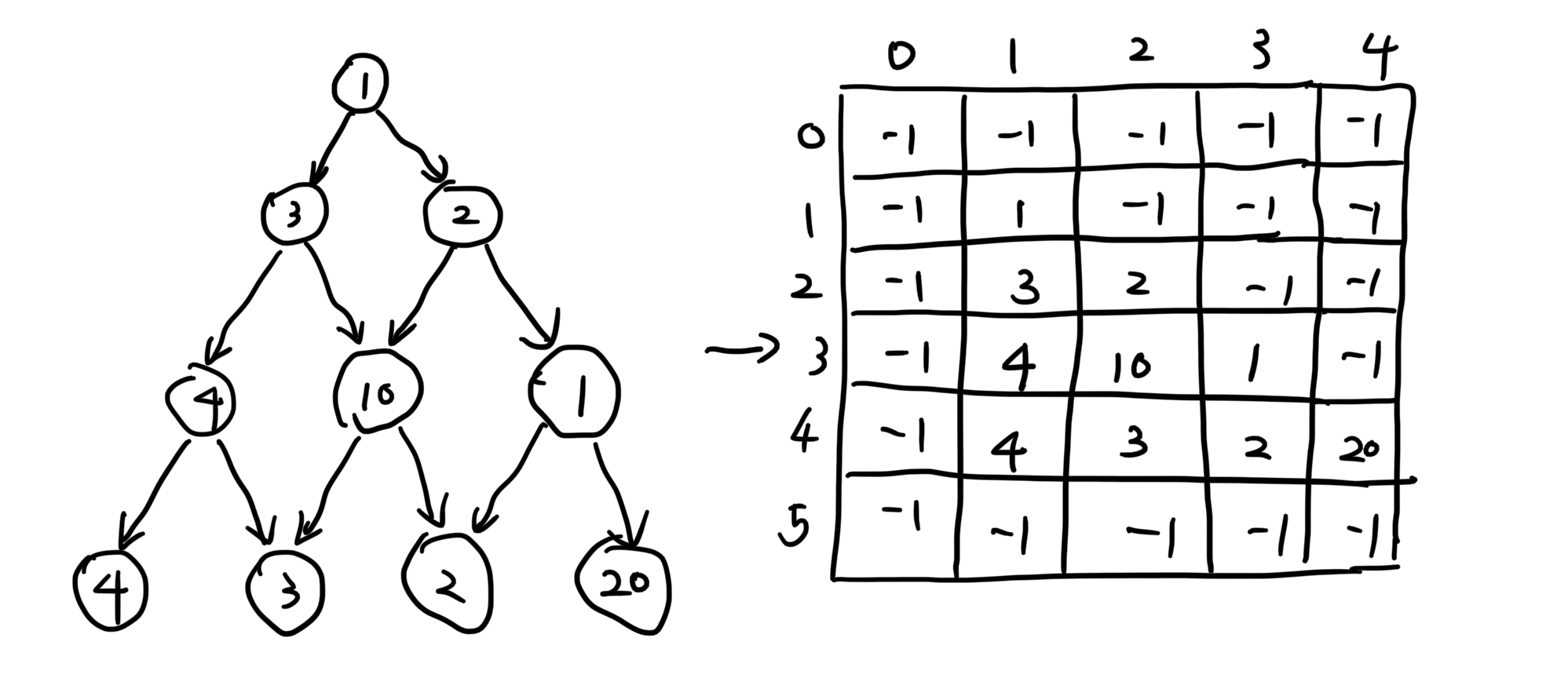
注意:第(0)行和第(0)列是不需要的,因为不好计算。第(k)行有(k)个数。
像这种结构找最大或者最小值,一般就是用深搜,每条路径都要遍历一遍。确定了深搜之后,想一下输入的问题,我以为这道题的输入是给定(n),输入这(n)个数。所以现在要解决的问题是(n)个数一共是多少层:假设(n)个数一共可以组成(k)层(假设是满的),第(1)层有(1)数...第(k)层有(k)个数,则一定有:
左边就是个等差数列,结果为:
展开可得:
这里求解(k),根据韦达定理,可知:
同过这个公式可以求得(k):
因为(k_2)一定是小于(0)的,所以(k_1)为最终答案,但此时一定是满的,需要求解的层数进行上取整ceil()。
深搜代码
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
#include <vector>
#include <map>
#include <cmath>
#include <deque>
using namespace std;
#define MAX_N 100
#define print(a) {
for (int i = 0; i < 10; i++) {
for (int j = 0; j < 10; j++) {
cout << grid[i][j] << " ";
}
cout << endl;
}
}
int n, grid[MAX_N + 5][MAX_N + 5], ans = 0;
int k;
void dfs(int x, int y, int sum) {
sum += grid[x][y];
// cout << "(" << x << ", " << y << ")" << " " << sum << endl;
if (x == k) {
ans = max(sum, ans);
return ;
}
if (grid[x + 1][y] >= 0) {
dfs(x + 1, y, sum);
}
if (grid[x + 1][y + 1] >= 0) {
dfs(x + 1, y + 1, sum);
}
}
void solve() {
memset(grid, -1, sizeof(grid));
cin >> n;
k = ceil((sqrt(1 + 8 * n) - 1) / 2);
cout << "k = " << k << endl;
for (int i = 1; i <= k; i++) {
for (int j = 1; j <= i; j++) {
cin >> grid[i][j];
// print(grid);
}
}
dfs(1, 1, 0);
cout << ans << endl;
}
int main() {
solve();
return 0;
}
思考过程2
深搜是暴力算法,相当于把所有的路径都走了一遍,如果是n层的树,一共会有(2^{n-1})条路径,所以当数据量很大的时候,算法所需要的时间很长,时间复杂度很高。
下面换一种思路,用dp。dp最重要的是确定状态和状态转移方程。当前这道题每一个点都是一个状态dp[i][j],这个状态代表以这个点为终点,从第一层起点到达当前这个点和的最大值。所有的点组成了一个状态空间,也就是答案的集合,遍历状态空间中的最大值就可以找到答案。
可以通俗的理解状态就是dp[i][j]数组。
确定了状态以后,那如何确定状态转移方程呢?这样想,随便找一个当前的状态dp[i][j],这个状态等于什么?也就是到达当前这个点的和的最大值等于什么呢?一定是等于当前这个点的grid[i][j]加上上一个状态的最大值,上一个状态是什么?就是上一层的与(i, j)相连接的点的状态最大值(可能有拗口,多读两遍好好理解一下)。
为什么这么做一定就正确呢?
因为是一个递归的过程,上一层的和的最大值加上当前层值,一定可以得到当前层的每一个点的和的最大值。所以dp数组维护的是每一层和值的最大值。
根据前面的思路可以得到状态转移方程:
dp代码1
/*************************************************************************
> File Name: test.cpp
> Author: lihanwen
> Mail: 18646139976@163.com
> Created Time: 六 6/12 14:36:38 2021
> Description:
************************************************************************/
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
#include <vector>
#include <map>
#include <cmath>
#include <deque>
#include <ctime>
using namespace std;
#define MAX_N 100
#define print(a) {
for (int i = 1; i <= k; i++) {
for (int j = 1; j <= k; j++) {
cout << a[i][j] << " ";
}
cout << endl;
}
}
int n, grid[MAX_N + 5][MAX_N + 5], ans = 0;
int k;
int dp[MAX_N + 5][MAX_N + 5];
void solve() {
memset(grid, -1, sizeof(grid));
memset(dp, -1, sizeof(dp));
cin >> n;
k = ceil((sqrt(1 + 8 * n) - 1) / 2);
for (int i = 1; i <= k; i++) {
for (int j = 1; j <= i; j++) {
cin >> grid[i][j];
}
}
clock_t start = clock();
// 初始化dp数组
dp[1][1] = grid[1][1];
// 构造dp数组
for (int i = 2; i <= k; i++) {
for (int j = 1; j <= i; j++) {
dp[i][j] = grid[i][j] + max(dp[i - 1][j - 1], dp[i - 1][j]);
}
}
for (int i = 1; i <= k; i++) {
ans = max(ans, dp[k][i]);
}
clock_t end = clock();
cout << std::fixed << "use time : " << (double)(end - start) / CLOCKS_PER_SEC << "s" << endl;
cout << ans << endl;
}
int main() {
solve();
return 0;
}
代码说明:
- 因为题目中说的是全部为非负整数,所以代码中初始化的时候全部初始化成(-1),在维护
dp数组的时候并没有确定边界,为什么不用确定边界?例如在i = 2, j = 1时,i - 1 = 1, j - 1 = 0,dp[1][0] == -1,并且i - 1 = 1, j = 1,dp[i - 1][j] == dp[1][1],dp[1][1]一定是大于(-1)的,所以,不需要判断边界。 - 最终答案一定是在
dp数组的最后一行,找到最大。