位运算
百度百科如下:
程序中的所有数在计算机内存中都是以二进制的形式储存的。位运算就是直接对整数在内存中的二进制位进行操作
位操作的优势
- 位运算是一种底层的运算,往往比我们普通的运算要快上许多许多
- 位运算是最高效而且占用内存最少的算法操作,执行效率非常高
- 位运算操作的是二进制数,会拥有一些二进制的特性,在实际问题可以方便运用
- 位运算只需较低的空间需求
- 位运算使用能使程序变得更加简洁和优美
- 位运算可以表示一些状态集合
运算符号
下面的a和b都是整数类型,则
| 含义 | C语言 |
|---|---|
| 按位与 | a & b |
| 按位或 | a | b |
| 按位异或 | a ^ b |
| 按位取反 | ~a |
| 左移 | a << b |
| 带符号右移 | a >> b |
| 无符号右移 |
优先级
C语言中位运算符之间,按优先级顺序排列为
| 优先级 | 符号 |
|---|---|
| 1 | ~ |
| 2 | <<、>> |
| 3 | & |
| 4 | ^ |
| 5 | | |
| 6 | &=、^=、|=、<<=、>>= |
概念简介以及技巧
本文会以C语言的交互环境来做代码演示
常见的二进制位的变换操作
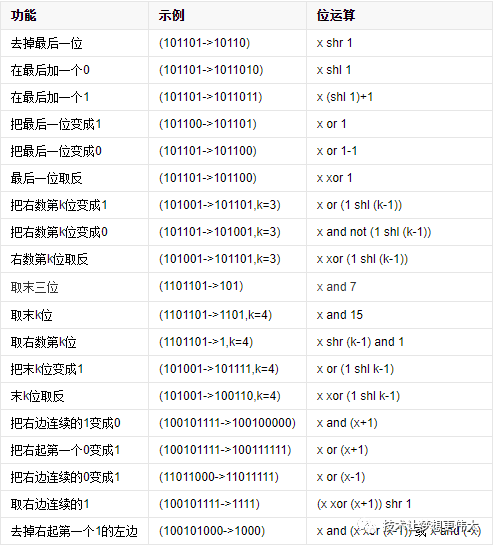
and运算 &
- 判断奇偶数
对于除0以外的任意数x,使用x&1==1作为逻辑判断即可
if (x&1==1) { }
- 判断某个二进制位是否为1
比如第7位, 0x40转到二进制是0100 0000,代表第7位是1.
if (n&0x40) { //TODO:添加你要处理的代码 }
- 字节读取
(x >> 0) & 0x000000ff /* 获取第0个字节 */ (x >> 8) & 0x000000ff /* 获取第1个字节 */ (x >> 16) & 0x000000ff /* 获取第2个字节 */ (x >> 24) & 0x000000ff /* 获取第3个字节 */
- 判断一个数是不是 2 的指数
bool isPowerOfTwo(int n) { if (n <= 0) return false; return (n & (n - 1)) == 0; }
- 取余,(除数为2的n次方)
//得到余数 int Yu(int num,int n) { int i = 1 << n; return num&(i-1); }
- 指定二进制位数截取
比如说16位二进制数A:1001 1001 1001 1000,如果来你想获A的哪一位的值,就把数字B:0000 0000 0000 0000的那一位设置为1.
比如说我想获得A的第三位就把B的第三位数字设置为1,则B为0000 0000 0000 0100,设置完之后再把A、B求与, 其结果若为0,说明A的第三位为0,其结果为1,说明A的第三位为1.
同理:若要获得A的第五位,就把B设置为0000 0000 0001 0000,之后再求与。
通常在我们的程序中,数字B被称为掩码,其含义是专门用来测试某一位是否为0的数值。
- 统计二进制中 1 的个数
利用x=x&(x-1),会将x用二进制表示时最右边的一个1变为0,因为x-1会将该位变为0.
int Count(int x) { int sum=0; while(x) { sum++; x=x&(x-1); } return sum; }
or操作
- 生成组合编码,进行状态压缩
当把二进制当作集合使用时,可以用or操作来增加元素。合并编码 在对字节码进行加密时,加密后的两段bit需要重新合并成一个字节,这时就需要使用or操作。
- 求一个数的二进制表达中0的个数
int Grial(int x) { int count = 0; while (x + 1) { count++; x |= (x + 1); } return count; }
xor操作
- 两个整数交换变量名
void swap(int &a, int &b) { a ^= b; b ^= a; a ^= b; }
- 判断两个数是否异号
int x = -1, y = 2; bool f = ((x ^ y) < 0); // true int x = 3, y = 2; bool f = ((x ^ y) < 0); // false
- 数据加密
将需要加密的内容看做A,密钥看做B,A ^ B=加密后的内容C。而解密时只需要将C ^ 密钥B=原内容A。如果没有密钥,就不能解密!
#include <stdio.h> #include <stdlib.h> #include <string.h> #define KEY 0x86 int main() { char p_data[16] = {"Hello World!"}; char Encrypt[16]={0},Decode[16]={0}; int i; for(i = 0; i < strlen(p_data); i++) { Encrypt[i] = p_data[i] ^ KEY; } for(i = 0; i < strlen(Encrypt); i++) { Decode[i] = Encrypt[i] ^ KEY; } printf("Initial date: %s ",p_data); printf("Encrypt date: %s ",Encrypt); printf("Decode date: %s ",Decode); return 0; }
- 数字判重
利用了二进制数的性质:x^y^y = x。我们可见,当同一个数累计进行两次xor操作,相当于自行抵销了,剩下的就是不重复的数
- 找出没有重复的数
int find(int[] arr){ int tmp = arr[0]; for(int i = 1;i < arr.length; i++){ tmp = tmp ^ arr[i]; } return tmp; }
not操作
- 交换符号
int reversal(int a) { return ~a + 1; }
- 取绝对值(效率高)
- n>>31 取得n的符号
- 若n为正数,n>>31等于0
- 若n为负数,n>>31等于-1
- 若n为正数 n^0=0,数不变
- 若n为负数,有n^-1 需要计算n和-1的补码,然后进行异或运算,结果n变符号并且为n的绝对值减1,再减去-1就是绝对值
int abs(int n) { return (n ^ (n >> 31)) - (n >> 31); }
也可以这样使用
int abs(int n) { int i = n >> 31; return i == 0 ? n : (~n + 1); }
- 从低位到高位.将n的第m位置1
将1左移m-1位找到第m位,得到000...1...000, n在和这个数做或运算
int setBitToOne(int n, int m) { return n | (1 << (m-1)); }
同理从低位到高位,将n的第m位置0,代码如下
int setBitToZero(int n, int m) { return n & ~(1 << (m-1)); }
shl操作 & shr操作
- 求2的N次方
1<<n
- 高低位交换
unsigned short a = 34520; a = (a >> 8) | (a << 8);
- 进行二进制逆序
unsigned short a = 34520; a = ((a & 0xAAAA) >> 1) | ((a & 0x5555) << 1); a = ((a & 0xCCCC) >> 2) | ((a & 0x3333) << 2); a = ((a & 0xF0F0) >> 4) | ((a & 0x0F0F) << 4); a = ((a & 0xFF00) >> 8) | ((a & 0x00FF) << 8);
- 获得int型最大最小值
int getMaxInt() { return (1 << 31) - 1;//2147483647, 由于优先级关系,括号不可省略 } int getMinInt() { return 1 << 31;//-2147483648 }
- m的n次方
//自己重写的pow()方法 int pow(int m , int n){ int sum = 1; while(n != 0){ if(n & 1 == 1){ sum *= m; } m *= m; n = n >> 1; } return sum; }
- 找出不大于N的最大的2的幂指数
int findN(int n){ n |= n >> 1; n |= n >> 2; n |= n >> 4; n |= n >> 8 // 整型一般是 32 位,上面我是假设 8 位。 return (n + 1) >> 1; }
- 二分查找32位整数的前导0个数
int nlz(unsigned x) { int n; if (x == 0) return(32); n = 1; if ((x >> 16) == 0) {n = n +16; x = x <<16;} if ((x >> 24) == 0) {n = n + 8; x = x << 8;} if ((x >> 28) == 0) {n = n + 4; x = x << 4;} if ((x >> 30) == 0) {n = n + 2; x = x << 2;} n = n - (x >> 31); return n; }
- 位图的操作
将 x 的第 n 位置1,可以通过 x |= (x << n) 来实现
set_bit(char x, int n);
将 x 的第 n 位清0,可以通过 x &= ~(1 << n) 来实现
clr_bit(char x, int n);
取出 x 的第 n 位的值,可以通过 (x >> n) & 1 来实现
get_bit(char x, int n);
如下:
#define clr_bit(x, n) ( (x) &= ~(1 << (n)) ) #define set_bit(x, n) ( (x) |= (1 << (n)) ) #define get_bit(x, n) ( ((x)>>(n)) & 1 )
综合应用
以下仅列出,感兴趣可以参考下面链接.
关于操作计数方法
计算整数的符号
检测两个整数是否具有相反的符号
计算无分支的整数绝对值(abs)
计算两个整数的最小值(最小值)或最大值(最大值),而无需分支
确定整数是否为2的幂
标志延伸
- 从恒定位宽扩展的符号
- 从可变位宽扩展的符号
- 通过3个操作从可变位宽扩展符号 有条件地设置或清除位而不分支
有条件地否定一个值而不分支
根据掩码合并两个值中的位
计数位设置
- 计数位设置,幼稚的方式
- 计算由查找表设置的位
- 数位集,Brian Kernighan的方式
- 使用64位指令对14、24或32位字中设置的位进行计数
- 并行设置计数位
- 从最高有效位到给定位置的计数位的设置(等级)
- 从给定的计数(等级)中选择位位置(从最高有效位开始)
计算奇偶校验(如果设置了奇数位数,则为1,否则为0)
- 天真地计算单词的奇偶性
- 通过查找表计算奇偶校验
- 使用64位乘法和模数除法计算字节的奇偶校验
- 用乘法计算单词的奇偶校验
- 并行计算奇偶校验
交换价值
- 用减法和加法交换值
- 用XOR交换值
- 用XOR交换单个位
反转位序列
-
反转位是显而易见的方式
- 逐字查找表中的位反转
- 通过3个操作(64位乘法和模数除法)反转字节中的位
- 通过4个操作反转字节中的位(64位乘法,无除法)
- 通过7个操作反转字节中的位(无64位,仅32位)
- 与5 * lg(N)个运算并行地反转N位数量
模数除法(又名计算余数)
- 在不进行除法运算的情况下,将模数除以1 << s(显而易见)
- 在不进行除法运算的情况下以(1 << s)-1计算模数除法
- 不进行除法运算就并行计算(1 << s)-1的模数除法
查找整数的整数对数2(又称最高位集的位置)
- 使用O(N)运算找到MSB N设置为整数的对数2(显而易见的方法)
- 查找具有64位IEEE浮点数的整数的整数对数2
- 使用查找表找到整数的对数2
- 在O(lg(N))运算中找到N位整数的对数2
- 使用乘法和查找在O(lg(N))操作中找到N位整数的对数2
查找整数的对数以10为底的整数
查找整数的整数对数10
查找32位IEEE浮点数的整数对数基数2
查找32位IEEE浮点的pow(2,r)根的整数对数基数2(对于无符号整数r)
计算连续的尾随零位(或查找位索引)
- 线性计算右边的连续零位(后缀)
- 并行计算右侧连续的零位(后缀)
- 通过二进制搜索计算右边连续的零位(跟踪)
- 通过强制转换为浮点数来计算右侧连续的零位(跟踪)
- 用模数除法和查找计算右边连续的零位(跟踪)
- 用乘法和查找计数右边连续的零位(后跟)
通过浮法舍入到2的下一个最高幂
向上舍入到2的下一个最高幂
交织位(也称为计算莫顿数)
- 交错位的明显方式
- 通过表查找交织位
- 带64位乘法的交织位
-
通过二进制幻数交错位
测试单词中的字节范围(并计算出现的次数)
- 确定单词是否为零字节
- 确定一个单词的字节数是否等于n
- 确定一个单词的字节数是否小于n
- 确定单词的字节数是否大于n
- 确定单词是否在m和n之间有一个字节
按词典顺序计算下一位排列
更多内容可以查看:
http://graphics.stanford.edu/~seander/bithacks.html
关注微信公众号『技术让梦想更伟大』,后台回复“m”查看更多内容,回复“加群”加入技术交流群。

长按前往图中包含的公众号关注