题意:长度为$1e9$的区间$A$下标为$[0,1e9-1]$,数输入$n$个区间,$[l_i,r_i]$区间类的值为1,其余为-1,问有多少区间和大于0.
题解:看了来自大佬的博客,能够产生贡献的点最多只有$3e7$个,意思是先求一个前缀和,然后画成图应该是这样。
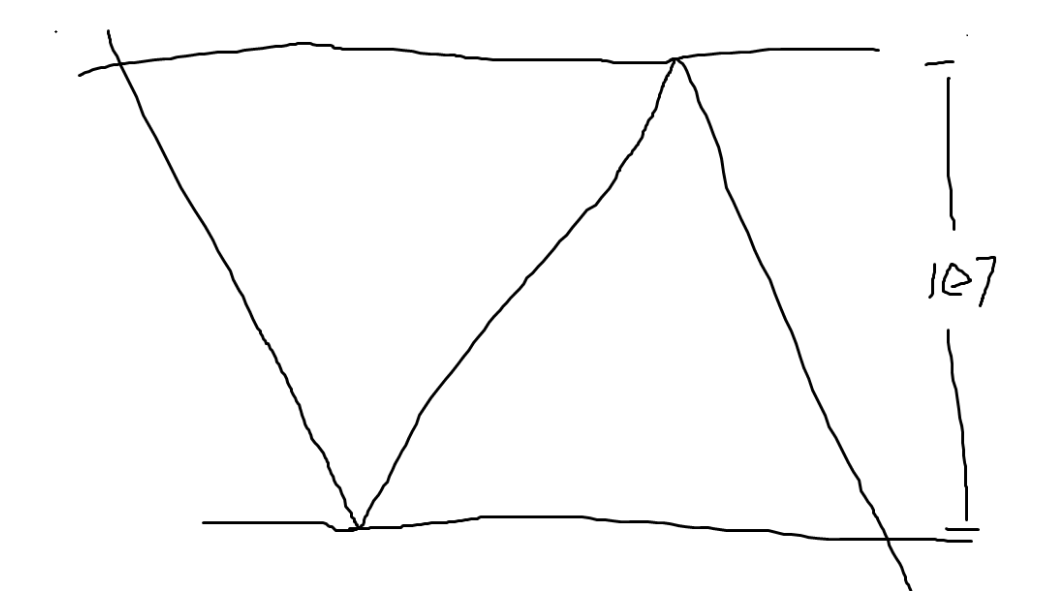
最差就是这样了,能够有影响的就只有这$3e7$个点 (可能是分段的) ,那么问题来了,怎么求出这$3e7$个点。
来自大佬的博客

为什么呢?在大佬眼里很简单,我画了个图才理解。
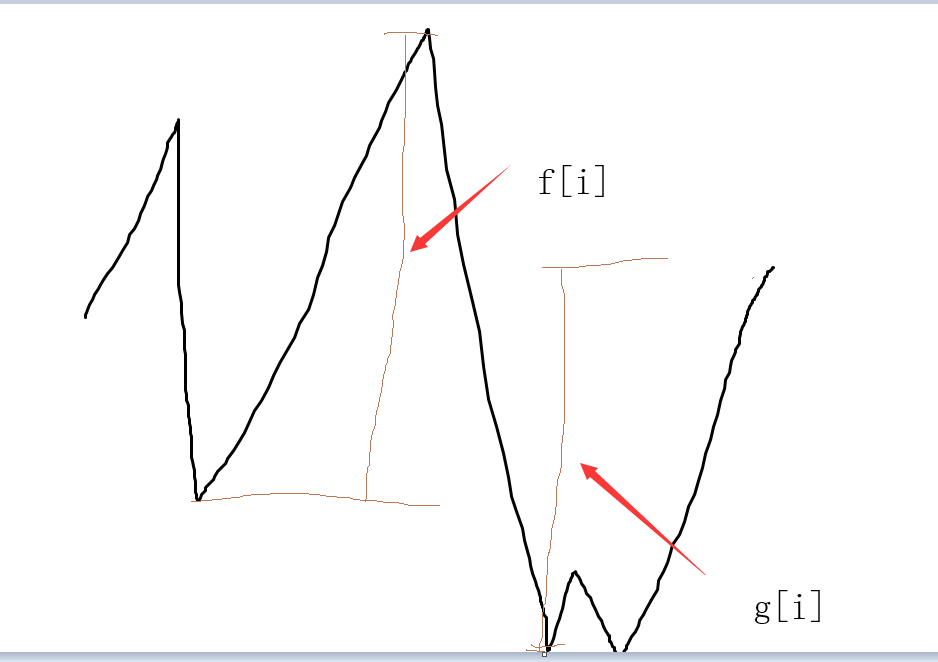
显然前面一个的$f[i]$加后面$g[i+1]$比两个区间之间的长度大就事连在一起的。(我果然太菜了)
然后处理完之后,就相当于处理
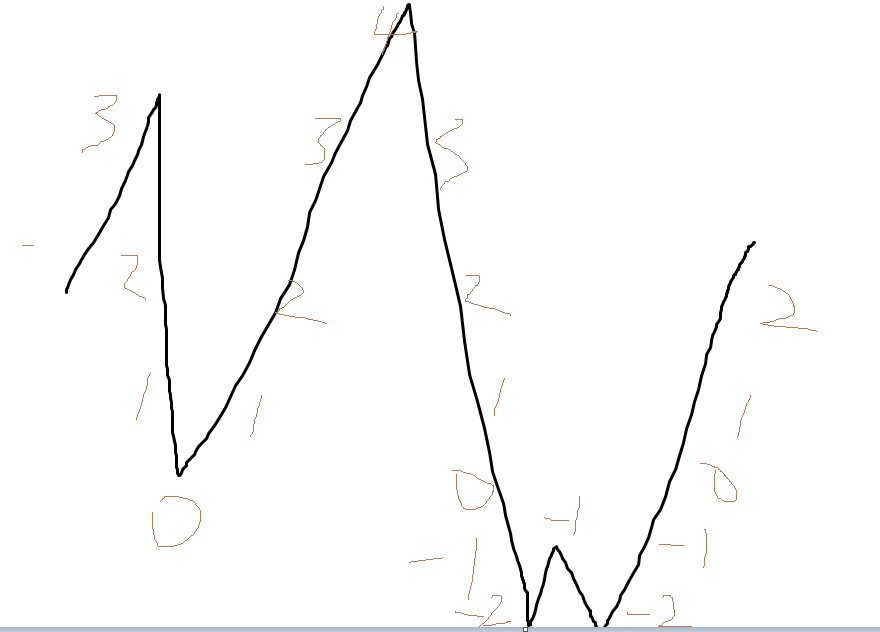
一个这样的前缀和,求所有位置有几个在他前面前缀比他小。如果范围小一点就用树状数组求一下就没了,$3e7log(3e7)$显然超时了。
看到这个前缀和,前后项最大只差了$1$,上下界最大差值不超过$3e7$,这再做个前缀和 sum 。用一个数组表示一个数字出现的次数,然后$sum[m]=sum[m-1]+b[m]$,更新前缀和,答案就是$ans+=sum[m-1]$。
中间有一些细节要处理
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
|
using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, int> P;
typedef long double ld;
#define VNAME(value) (#value)
#define bug printf("*********n");
#define debug(x) cout<<"["<<VNAME(x)<<" = "<<(x)<<"]"<<endl;
#define mid (l+r)/2
#define chl 2*k+1
#define chr 2*k+2
#define lson l,mid,chl
#define rson mid+1,r,chr
#define mem(a, b) memset(a,b,sizeof(a));
const long long mod = 1e9 + 7;
const int maxn = 1e6 + 5;
const int INF = 0x7fffffff;
const LL inf = 0x3f3f3f3f;
const double eps = 1e-8;
void () {
#ifndef ONLINE_JUDGE
freopen("../data.in", "r", stdin);
#endif
}
#ifndef ONLINE_JUDGE
clock_t start = clock();
#endif
int n;
LL l[maxn], r[maxn];
LL f[maxn], g[maxn];
struct node {
LL l, r, x;
} dat[maxn * 5];
LL sum[maxn * 30 + 20], b[maxn * 30 + 20];
int main() {
fin();
大专栏 2019牛客暑期多校训练营(第二场)J Subarray">scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%lld%lld", &l[i], &r[i]);
}
f[1] = r[1] - l[1] + 1;
for (int i = 2; i <= n; i++) {
f[i] = max(0LL, f[i - 1] - (l[i] - r[i - 1] - 1)) + r[i] - l[i] + 1;
}
g[n] = r[n] - l[n] + 1;
for (int i = n - 1; i >= 1; --i) {
g[i] = max(0LL, g[i + 1] - (l[i + 1] - r[i] - 1)) + r[i] - l[i] + 1;
}
int i = 1;
LL ans = 0;
while (i <= n) {
int j = i + 1;
LL mi = 0, mx = 0, pos = 0;
while (j <= n && g[j] + f[j - 1] >= l[j] - r[j - 1] - 1) {
j++;
}
j--;
int t = i, num = 1;
for (; t <= j; t++) {
if (num == 1)dat[num].l = 0;
else if (l[t] - r[t - 1] == 1) dat[num].l = pos + 1;
else dat[num].l = pos;
pos += r[t] - l[t] + 1;
dat[num].r = pos;
dat[num++].x = 1;
mx = max(mx, pos);
if (t != j) {
dat[num].r = pos - 1;
pos -= l[t + 1] - r[t] - 1;
dat[num].l = pos + 1;
dat[num++].x = 0;
mi = min(pos, mi);
} else {
dat[num].r = pos - 1;
dat[num].l = max(mi, pos - ((int) 1e9 - 1 - r[t]));
dat[num++].x = 0;
}
}
dat[0].r = min(mx, l[i]);
dat[0].l = 1;
dat[0].x = 0;
for (int k = 0; k <= mx - mi + 200; k++)b[k] = sum[k] = 0;
assert(mx - mi < maxn * 30);
for (int k = 0; k < num; ++k) {
dat[k].l += -mi;
dat[k].r += -mi;
if (dat[k].x == 1) {
for (int m = dat[k].l; m <= dat[k].r; ++m) {
b[m]++;
sum[m] = sum[m - 1] + b[m];
if (m >= 1)ans += sum[m - 1];
}
} else {
LL tmp = 0;
if (dat[k].l > 0)tmp = sum[dat[k].l - 1];
for (int m = dat[k].l; m <= dat[k].r; ++m) {
if (m >= 1)ans += tmp;
tmp = sum[m];
b[m]++;
sum[m] = sum[m - 1] + b[m];
}
}
}
i = j + 1;
}
printf("%lldn", ans);
#ifndef ONLINE_JUDGE
cout << "RUNTIME:" << (1.0 * clock() - start) / 1000 << "ms" << endl;
#endif
return 0;
}
|
给几组数据你去试试
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| 2
5 9
12 17
3
3 5
6 6
7 9
3
3 5
8 8
9 10
1
999999998 999999999
|



