神经网络一般有三层,输入层、隐含层以及输出层。输入值经过隐含层的作用,在输出层输出,其结果会与期望值作比较,这里用代价函数来衡量误差。神经网络的训练过程,按照我的理解就是通过调整权值和偏置,使代价函数降到最小的过程。
但是使用什么方法调整那些参数?之前讲过梯度,当我们站在半山腰中寻找下山最快的方向,我们只需要找到我们所处位置的梯度,沿着梯度反方向就能找到最快下山的路线。假设我们站在((x_0,,y_0))的位置,则该位置的梯度为((left. frac{partial f}{partial x} right|_{x=x_0,y=y_0},left. frac{partial f}{partial y} right|_{x=x_0,y=y_0})),那么下一刻你需要调整的位置为((x_0-left. frac{partial f}{partial x} right|_{x=x_0,y=y_0},y_0-left. frac{partial f}{partial y} right|_{x=x_0,y=y_0}))。这种方法叫梯度下降法,通过使用这种方法来调整权值和偏置,使代价函数降到最小。
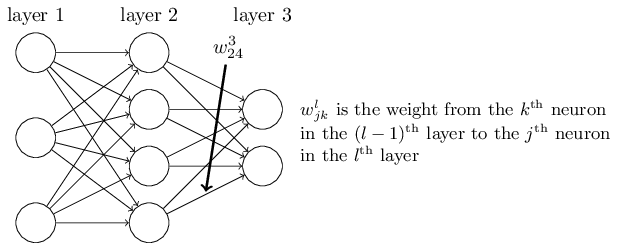
上图是一个三层的神经网络模型,第一层为输入层,第二层为隐含层,第三层为输出层。其中(,w_{jk}^l,)表示第(,l,)层第(,j,)个神经元与第(,l-1,)层第(,k,)个神经元之间的权值。
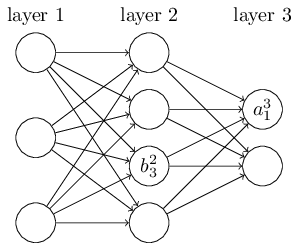
图二中(,a_j^l,)表示第(,l,)层第(,j,)个神经元的输出值,(,b_k^l,)表示第(,l,)层第(,k,)个神经元的偏置。设代价函数为(C_0),则有如下公式:
$$
begin{align}
C_0&=sum_{j=0}^{n_l-1}(a_j^l-y_j)^2
a_j^l&=sigma(z_j^l)
z_j^l&=sum_{k=0}^{n 大专栏 神经网络--反向传播算法_{l-1}-1}a_k^{l-1}w_{jk}^l+b_j^l
end{align}
$$
如果此时神经网络中的权值为((w_0,w_1…w_m)),那么我们需要找到代价函数(,C_0,)相对于此刻权值的梯度((frac{partial C_0}{partial w_0},frac{partial C_0}{partial w_1}…frac{partial C_0}{partial w_m}))。根据链式法则,有
$$
frac{partial C_0}{partial w_{jk}^l}=frac{partial C_0}{partial a_j^l}frac{partial a_j^l}{partial z_j^l}frac{partial z_j^l}{partial w_{jk}^l}
$$
其中
$$
begin{align}
frac{partial C_0}{partial a_j^l}&=2(a_j^l-y_j)
frac{partial a_j^l}{partial z_j^l}&=sigma’(z_j^l)
frac{partial z_j^l}{partial w_{jk}^l}&=a_k^{l-1}
end{align}
$$
所以
$$
frac{partial C_0}{partial w_{jk}^l}=2(a_j^l-y_j)sigma’(z_j^l)a_k^{l-1}
$$
同理
$$
begin{align}
frac{partial C_0}{partial b_j^l}&=2(a_j^l-y_j)sigma’(z_j^l)
frac{partial C_0}{partial a_k^{l-1}}&=2(a_j^l-y_j)sigma’(z_j^l)w_{jk}^l
end{align}
$$
但是对于(frac{partial C_0}{partial a_k^{l-1}}),由于(a_k^{l-1})的变化会影响到(,l,)层所有输出值,则
$$
begin{align}
frac{partial C_0}{partial a_k^{l-1}}&=sum_{j=0}^{n_l-1}frac{partial C_0}{partial a_j^l}frac{partial a_j^l}{partial z_j^l}frac{partial z_j^l}{partial a_{k}^{l-1}}
frac{partial C_0}{partial a_k^{l-1}}&=sum_{j=0}^{n_l-1}2(a_j^l-y_j)sigma’(z_j^l)w_{jk}^l
end{align}
$$
之前说过,神经网络的训练过程就是通过调整权值和偏置的值来使代价函数降到最小,那么此处求代价函数对于(,l-1,)层输出值的偏导有何意义?因为我们在求(frac{partial C_0}{partial w_{jk}^{l-1}})需要用到这个值。
$$
begin{align}
frac{partial C_0}{partial w_{jk}^{l-1}}&=frac{partial C_0}{partial a_j^{l-1}}frac{partial a_j^{l-1}}{partial z_j^{l-1}}frac{partial z_j^{l-1}}{partial w_{jk}^{l-1}}
&=sum_{j=0}^{n_l-1}2(a_j^l-y_j)sigma’(z_j^l)w_{jk}^l cdot sigma’(z_j^{l-1})w_{jk}^{l-1}
end{align}
$$
无论神经网络有多少层,都可以如此类推。到此,误差在各个层之间的传递以及各层间权值的调整已经很清楚了。
以上的代价函数和(,sigma,)函数可根据需求选取。