FFT学习笔记

FFT学习笔记

FFT，快速傅里叶变换，是一种在(O(nlog n))的时间内计算两个多项式乘积的算法。

前置芝士

复数

没学过的请自行翻阅高中数学选修2-2。

多项式的表示

给出一个多项式 $f(x) = a_0 + a_1x + a_2x^2 + ... + a_nx^n $

系数表示法

就是用一个系数序列来表达多项式，显然系数序列和多项式是一一对应的。

[f(x) = a_0 + a_1x + a_2x^2 + ... + a_nx^n Leftrightarrow f(x) = {a_0,a_1,a_2,...,a_n} ]

点值表示法

点值表示法是把这个多项式看成一个函数，从上面选取(n+1)个点，从而利用这 (n+1) 个点来唯一的表示这个函数。

正如解一个 (n) 元方程组需要 (n+1) 个方程一样，这 (n+1) 个点的序列显然也和多项式一一对应。

[f(x) = a_0 + a_1x + a_2x^2 + ... + a_nx^n Leftrightarrow f(x) = {(x_0,y_0),(x_1,y_1),(x_2,y_2),...,(x_n,y_n)} ]

--------------------分割线--------------------

这两种表示法各有优劣，系数表示法可以在 (O(n)) 的时间内求出一个 (f(x_0)) ，但计算多项式乘法时却需要 (O(n^2)) 的时间，点值表示法则正好相反。所以FFT的目的就是利用一些特殊的点，把复杂度均摊一下，变成 (O(nlog n))

单位复根

这是FFT降低复杂度的关键，因为单位复根有极为优秀的性质。

定义：

对于方程 (x^n = 1) 的复数解，称之为 (n) 次单位复根，显然这样的单位复根有 (n) 个。

其中一个可以表示为 $ omega_n = e^{frac{2pi i}{n}} $ 那么对于每一个单位复根，有$$ omega_n^k = e^{frac{2pi i k}{n}} $$

而根据欧拉公式，又有：

[omega_n = e^{frac{2pi i}{n}} = cos(frac{2 pi}{n}) + i · sin(frac{2 pi}{n}) ]

几何意义：

在一个单位圆中，把单位圆等分，几个等分点的坐标就是单位复根的向量。

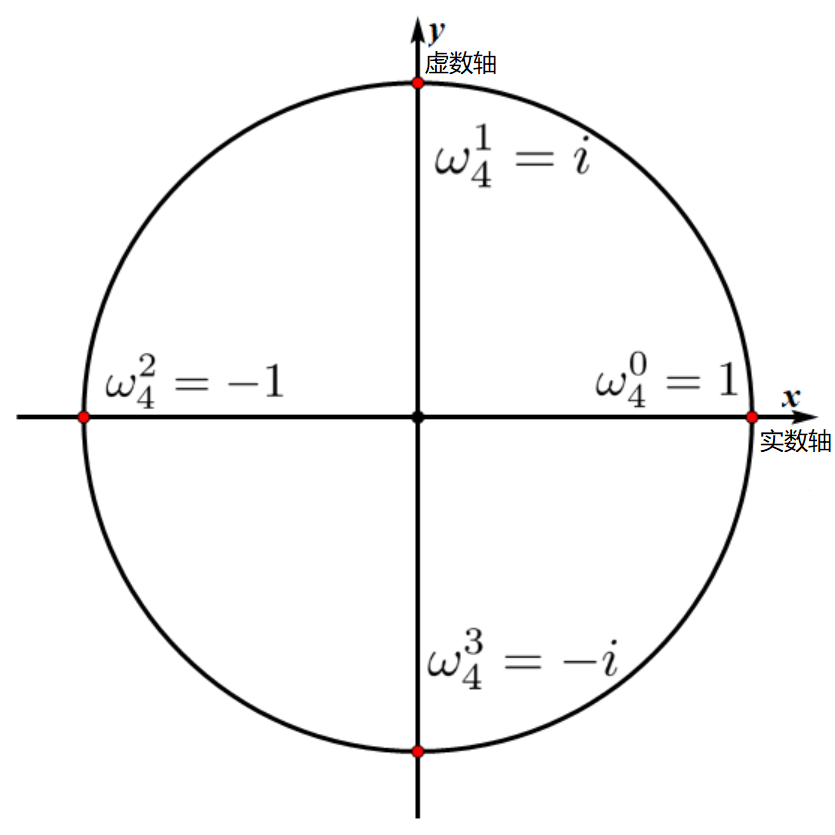
这个图就可以生动形象表示出来了。

单位根的性质

性质1：(omega_n^0 = 1)

这十分显然，看图就知道了。

性质2：(omega_n^k = omega_{2n}^{2k})

可以根据公式证明，或者几何意义也可直观理解。

性质3：(omega_n^{k+frac{n}{2}}=-omega_n^k)

仍然是代入公式证明即可。

这三个性质就是FFT降低复杂度的关键了。

快速傅里叶变换

离散傅里叶变换(DFT)

对于一个多项式 $f(x) = a_0 + a_1x + a_2x^2 + ... + a_{n-1}x^{n-1} $

为了便于操作，设 (n = 2^k)$ ，不足补0即可。

然后按照奇偶项分类，奇数项提出一个 (x)：

[f(x) = (a_0 + a_2x^2 + ... + a_{n-2}x^{n-2}) + x(a_1 + a_3x^2 + ... + a_{n-1}x^{n-2} ]

设两个新的多项式：

[g(x) = a_0 + a_2x + ... + a_{n-2}x^{frac{n}{2}} ]

[h(x) = a_1 + a_3x + ... + a_{n-1}x^{frac{n}{2}} ]

那么就可以得到：

[f(x) = g(x^2)+x·h(x^2) ]

设(DFT(f(x)))表示对 (f(x)) 进行DFT操作后得到的点值表示，则:

[DFT(f(x)) = DFT(g(x^2))+x·DFT(h(x^2)) ]

重要的步骤出现了！这时我们依次代入单位复根：

[DFT(f(omega_n^k)) = DFT(g((omega_n^k)^2))+omega_n^k·DFT(h((omega_n^k))^2)) ]

[DFT(f(omega_n^k)) = DFT(g(omega_n^{2k}))+omega_n^k·DFT(h(omega_n^{2k})) ]

[DFT(f(omega_n^k)) = DFT(g(omega_{frac{n}{2}}^{k}))+omega_n^k·DFT(h(omega_{frac{n}{2}}^{k})) ]

同理：

[DFT(f(omega_n^{k+frac{n}{2}})) = DFT(g(omega_{frac{n}{2}}^{k}))-x·DFT(h(omega_{frac{n}{2}}^{k})) ]

我们发现，只要我们求出了(DFT(g(omega_{frac{n}{2}}^{k}))) 和 (DFT(h(omega_{frac{n}{2}}^{k})))，就可以求出 (DFT(f(omega_n^k))) 和 (DFT(f(omega_n^{k+frac{n}{2}})))，而这是一个问题规模不断变小的子问题，直接递归就行了。

复杂度分析：

代入操作要进行 (n) 次，花费 (O(n)) 的时间，设单次操作复杂度为 (T(n))，则有：

[T(n) = 2T(frac{n}{2}) +O(n) ]

根据主定理，可得复杂度为 (O(n log n))

离散傅里叶逆变换(IDFT)

证明过程又臭又长，这里就不写了qwq。(参考链接)

只介绍算法：

对于一个点值序列：(f(x) = {(x_0,y_0),(x_1,y_1),(x_2,y_2),...,(x_n,y_n)})

进行的操作方法和DFT类似，只是每次代入(frac{1}{omega_n^k})即可。

化简一下：

(frac{1}{omega_n^k} = e^{-frac{2pi ik}{n}} = cos(frac{2 pi k}{n}) + i · sin(-frac{2 pi k}{n}))

我们注意到这个值和DFT代入的值仅仅只有符号上的区别，那么不妨定义一个变量(op)，当 (op) 取 (1) 时进行 DFT操作，取 (-1) 就是IDFT操作。

代码实现：

void fft(comp *f,int n,int op) // op=1 -> DFT,op=-1 -> IDFT
{
	if(n == 1) return;//递归边界
	for(int i = 0;i < n;++i) tmp[i] = f[i];
	for(int i = 0;i < n;++i)//奇偶分别处理
	{
		if(i & 1) f[i / 2 + n / 2] = tmp[i];
		else f[i / 2] = tmp[i];
	}
	comp *g = f,*h = f + n / 2;
	fft(g,n / 2,op);fft(h,n / 2,op);//递归
	comp w(cos(2 * pi / n),sin(2 * pi * op / n)),x(1,0);//单位根
	for(int k = 0;k < n / 2;++k)
	{
		tmp[k] = g[k] + x * h[k];
		tmp[k + n / 2] = g[k] - x * h[k];
		x *= w;
	}
	for(int i = 0;i < n;++i) f[i] = tmp[i];
    return;
}

好的最朴素的FFT就讲完了。

FFT优化

咕咕咕咕咕咕咕咕咕