一、计算模型
1.1 定义:
我们在思考和处理算法的时候是机器无关、实现语言无关的。所有的算法运行在一种“抽象的机器”之上,这就是计算模型。
1.2 种类
图灵机是最有名的计算模型,本课使用更简单更合适的RAM计算模型。
1.3 RAM(Random Access Machine)模型
RAM模型的基本构成如下:
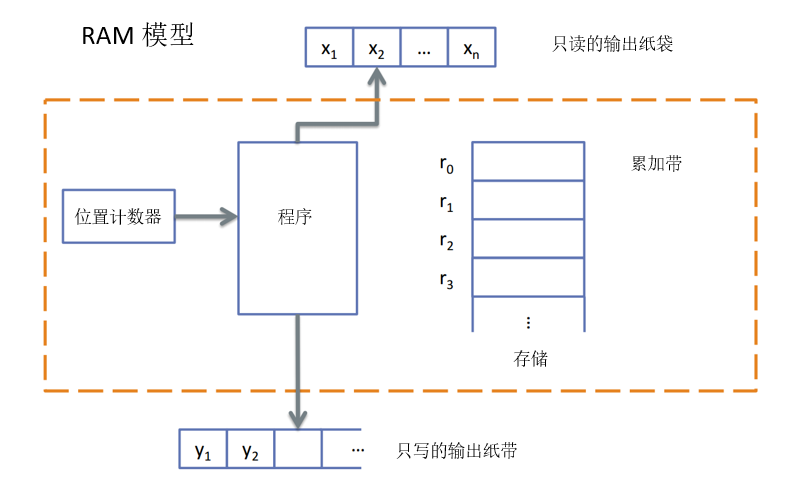
RAM计算模型有如下特点:
- 一个简单操作花费一步:键值比较、加减、内存访问
- 没有操作可以被分解:循环、子程序
- 内存:访存是一个简单操作、无限制的内存
二、算法设计
2.1 算法问题规约
将算法问题严格的定义为精确限定输入输出的“规约”形式:
- 输入:明确定义了算法接受的所有合法输入
- 输出:明确定义了对于每一个合法的输入值,相应的输出值应该是什么
例子1:
Euclid算法,辗转相除法的算法实现,计算m、n的最大公约数
输入:非负整数m,n
输出:gcd(m,n)

int Euclid(int m, int n) { if (m <= n) swap(m,n); while (m%n != 0) { n = m%n; m = n; } return n; } //这是测试用例 int main() { cout << Euclid(15,12) << endl; system("pause"); return 0; }
例子2:
顺序搜索,在一个数组中搜寻一个具体的数
输入:关键字K,数组E[1...n]
输出:如果K在E中,返回K在E中的位置,如果不在则返回-1

int SequentialSearch(vector<int> e, int k) { for (int i = 0; i < e.size(); ++i) if (k == e[i]) return i; return -1; } //这是测试用例 int main() { vector<int> e = {1,2,3,4,5,6}; cout << SequentialSearch(e,8) << endl; system("pause"); return 0; }
2.2 算法正确性的证明:数学归纳法
EUCLID算法正确性的证明:
当n=0时,对于任何m,有Euclid(m,0)=0
假设当n<=N时成立,考虑n=N+1的情况:
先有Euclid(m, N+1) = Euclid(N+1, m mod (N+1) ) ,而m mod(N+1)<=N恒成立,根据假设可知Euclid(N+1, m mod (N+1) )总能得出正确的答案,即n=N+1得证。
三、算法分析
3.1 算法的性能指标
- 时间复杂度
- 空间复杂度
在RAM中,时间复杂度使用RAM中执行简单操作的个数衡量,空间复杂度使用RAM中寄存器的个数来衡量。这样,对算法的性能分析变成了一个计数问题。由于RAM是抽象的,所以我们的衡量指标也是机器无关、语言无关的。
3.2 最坏情况复杂度
最坏复杂度的含义是最坏的输入对于的复杂度
例子:
在顺序搜索之中,待搜索的数k在数组e的位置越靠后,所需要搜寻的次数也就越多,当k在e的最后一个,此时为最坏情况。
3.3 平均情况复杂度
仅仅靠最坏情况时间复杂度不能充分代表算法性能。可以采用平均情况下的复杂度。
- 明确算法所有输入的分布情况
- 计算期望
例子:
对于顺序搜索的问题,给定数组为E[],长度为n,搜寻目标为K,假设所有输入情况等概率的出现。则成功的平均概率应该如下:
![]()
