跳表数据结构

§1 Skip List 介绍

§2 Skip List 定义以及构造步骤

§3 Skip List 完整实现

§4 Skip List 时间复杂度分析

§1 Skip List 介绍

Skip List是一种随机化的数据结构，基于并联的链表，其效率可比拟于二叉查找树（对于大多数操作需要O(log n)平均时间）。基本上，跳跃列表是对有序的链表增加上附加的前进链接，增加是以随机化的方式进行的，所以在列表中的查找可以快速的跳过部分列表(因此得名)。所有操作都以对数随机化的时间进行。Skip List可以很好解决有序链表查找特定值的困难。

§2 Skip List 定义以及构造步骤

Skip List定义

像下面这样（初中物理经常这样用，这里我也盗用下）：

一个跳表，应该具有以下特征：

1. 一个跳表应该有几个层（level）组成；
2. 跳表的第一层包含所有的元素；
3. 每一层都是一个有序的链表；
4. 如果元素x出现在第i层，则所有比i小的层都包含x；
5. 第i层的元素通过一个down指针指向下一层拥有相同值的元素；
6. 在每一层中，-1和1两个元素都出现(分别表示INT_MIN和INT_MAX)；
7. Top指针指向最高层的第一个元素。

构建有序链表

的一个跳跃表如下：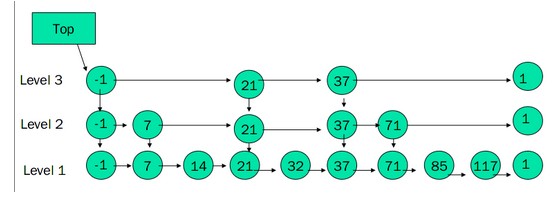 

Skip List构造步骤：

       1、给定一个有序的链表。

2、选择连表中最大和最小的元素，然后从其他元素中按照一定算法（随机）随即选出一些元素，将这些元素组成有序链表。这个新的链表称为一层，原链表称为其下一层。
3、为刚选出的每个元素添加一个指针域，这个指针指向下一层中值同自己相等的元素。Top指针指向该层首元素
4、重复2、3步，直到不再能选择出除最大最小元素以外的元素。

 一、查找

   目的：在跳跃表中查找一个元素x
   在跳跃表中查找一个元素x，按照如下几个步骤进行：
      1. 从最上层的链（Sh）的开头开始
      2. 假设当前位置为p，它向右指向的节点为q（p与q不一定相邻），且q的值为y。将y与x作比较
          (1) x=y  输出查询成功及相关信息
          (2) x>y  从p向右移动到q的位置
          (3) x<y  从p向下移动一格

      3. 如果当前位置在最底层的链中（S0），且还要往下移动的话，则输出查询失败

 

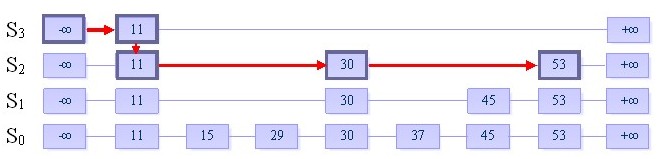
二、插入
     目的：向跳跃表中插入一个元素x
     首先明确，向跳跃表中插入一个元素，相当于在表中插入一列从S0中某一位置出发向上的连续一段元素。有两个参数需要确定，即插入列的位置以及它的“高度”。
     关于插入的位置，我们先利用跳跃表的查找功能，找到比x小的最大的数y。根据跳跃表中所有链均是递增序列的原则，x必然就插在y的后面。
     而插入列的“高度”较前者来说显得更加重要，也更加难以确定。由于它的不确定性，使得不同的决策可能会导致截然不同的算法效率。为了使插入数据之后，保持该数据结构进行各种操作均为O(logn)复杂度的性质，我们引入随机化算法（Randomized Algorithms）。

     我们定义一个随机决策模块，它的大致内容如下：

 产生一个0到1的随机数r     r ← random() 
如果r小于一个常数p，则执行方案A，  if  r<p then do A 
否则，执行方案B         else do B 
     初始时列高为1。插入元素时，不停地执行随机决策模块。如果要求执行的是A操作，则将列的高度加1，并且继续反复执行随机决策模块。直到第i次，模块要求执行的是B操作，我们结束决策，并向跳跃表中插入一个高度为i的列。

     我们来看一个例子：
     假设当前我们要插入元素“40”，且在执行了随机决策模块后得到高度为4
     步骤一：找到表中比40小的最大的数，确定插入位置

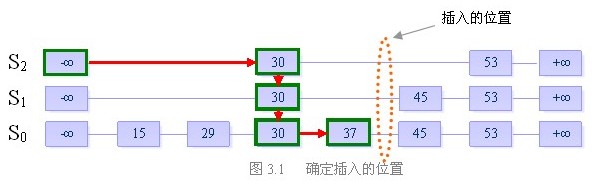
步骤二：插入高度为4的列，并维护跳跃表的结构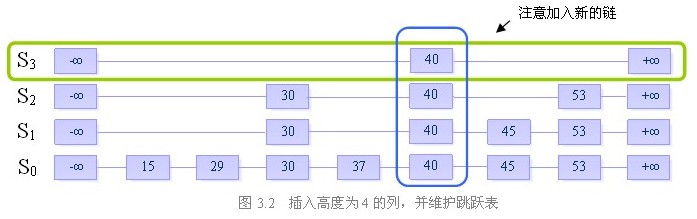 

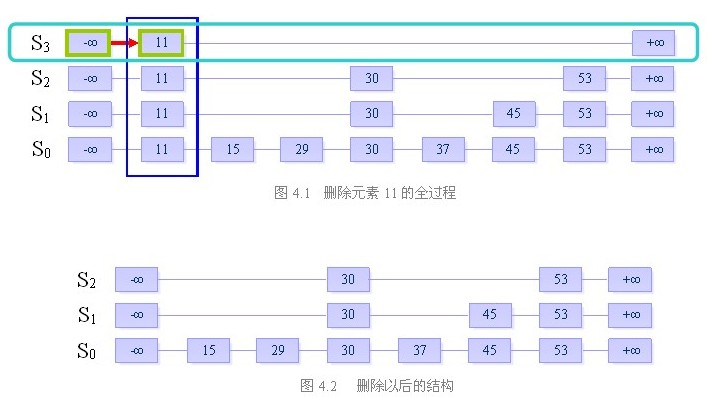
三、删除

    目的：从跳跃表中删除一个元素x
    删除操作分为以下三个步骤：

在跳跃表中查找到这个元素的位置，如果未找到，则退出 
将该元素所在整列从表中删除 
将多余的“空链”删除 

§3 Skip List 完整实现

 

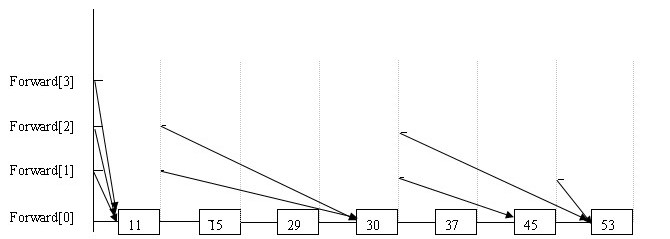
§4 Skip List 时间复杂度分析

这里计算时间复杂度的时候以Redis的源码为准，生成随机层数的源码是：

int zslRandomLevel(void) {
    int level = 1;
    while ((random()&0xFFFF) < (ZSKIPLIST_P * 0xFFFF))
        level += 1;
    return (level<ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL;
}

这里假设 ZSKIPLIST_P 为2 (实际为4,便于理解设置为2),这段代码我们可以理解为,落到层数为i + 1的概率为0.5^i

而反过来理解,每两个节点出现层数为2的期望就是1,每4个节点出现第三层的期望也为1,每8个节点出现第四层(0.5^3)的期望为1 (期望值 = 单个概率 * 数量)

正是基于此,如果我们的数据量越大,越是可以接近期望的值,所以,我们可以认为,我们实现了 "如果每2^i个节点都指向前面2^i个节点"的效果,也就是说,查找的平均复杂度为O(logN)