2020牛客暑期多校训练营（第一场）Easy Integration

传送门：J. Easy Integration

题意：给你n，求这个积分，最后的结果分子是记为p，分母记为q。

求（p*q^-1）mod 998244353。

题解：比赛完看到巨巨说这是贝塔函数，我一搜还真是。

贝塔函数的递推公式：

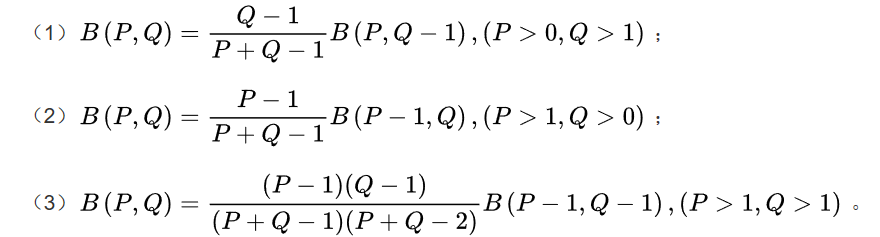
但是菜鸡只会打表找规律。那么说说怎么找到的规律吧。

先把所有的分子分母都找到，这个要用到（x-1）^n=C(n,0)x^n(-1)^0+C(n,1)x^(n-1)(-1)^1+C(n,2)x^(n-2)(-1)^2+……+C(n,n)x^0(-1)^n   ，(-1)^x 从0到n变成从n到0就变成了 (1-x)^n 的公式了。把分母都输出，发现分母是从(n+1)到(2n+1)连续的数，相乘就是 n! / (2n+1)! 。然后把分式通分，求出所有的分子相加，输出分子的和会发现分子就是 n! 。所以这个分式就是 n!*n! / (2n+1)! 。这里应该会用到费马小定理，拓展欧几里得也可以，我这里用的是费马小定理。

#include<bits/stdc++.h>
#define ll long long
#define pb push_back
#define ft first
#define sd second
using namespace std;

ll fac[2000100],inv[2000100];
const ll mod=998244353;
const ll N=2e6+10;
ll a[1001000],b[1000100];

ll quick(ll a,ll b)
{
    ll res=1;
    a=a%mod;
    while(b){
        if(b&1) res=(res*a)%mod;
        a=(a*a)%mod;
        b>>=1;
    }
    return res%mod;
}

void init()
{
    fac[0]=inv[0]=inv[1]=1;
    for(ll i=1;i<=N;i++)
        fac[i]=fac[i-1]*i%mod;
    for(ll i=2;i<=N;i++)
        inv[i]=(mod-mod/i)*inv[mod%i]%mod;
    for(ll i=1;i<=N;i++)
        inv[i]=inv[i-1]*inv[i]%mod;
}
ll C(ll n,ll m)
{
    return fac[n]*inv[m]%mod*inv[n-m]%mod;
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    init();
    ll n;
    while(cin>>n){
/**打表找规律

        ll p=0,q=1;
        for(ll i=0;i<=n;i++){
            a[i]=C(n,i);
            b[i]=n-i+n+1;
            a[i]%=mod;
            b[i]%=mod;
            if((n-i)&1) a[i]=-a[i];
            q*=b[i];
            q%=mod;
            cout<<b[i]<<' ';
        }
        cout<<endl;
        for(ll i=0;i<=n;i++){
            p+=q*a[i]%mod*quick(b[i],mod-2);
            p%=mod;
        }
        cout<<p<<endl;
        ll x=__gcd(p,q);
        p/=x,q/=x;
        ll ans=(p*quick(q,mod-2))%mod;
        cout<<ans<<endl;

**/
        ll p=fac[n]*fac[n]%mod;
        ll q=fac[2*n+1];
        cout<<p*quick(q, mod-2)%mod<<endl;
    }
    return 0;
}