python数据分析与算法之三 顺序表和链表

3.1内存

• 计算机的作用

  • 对二进制数据进行存储和运算

• 问题 :计算机如何计算 "1+2"

  • 将1和2的二进制形式的数据加载到计算机中进行存储，计算机才可以使用相关的寄存器对数据展开相关的运算

• 变量的概念

  • 变量其实表示的就是内存地址

  • 每一块内存空间都会有两个默认的属性

    • 地址：是用16进制的数来表示的。地址是用来让cpu进行寻址

    • 大小 : 衡量计算机内存空间大小的单位

      • bit (位)

      • bytes(字节) 1 bytes = 8 bit

      • kb 1 kb = 1024 bytes

      • mb 1 Mb = 1024 kb

      • Gb 1 Gb = 1024 mb地址：是用16进制的数来表示的。地址是用来让cpu进行寻址

• 引用和指向:

  • 引用 : 就是我们所说的变量

  • 指向 : 如果某一个引用或者变量存储在了某一块内存空间的地址后,则表示该引用(变量)指向了那块内存。

    • 一个变量指向了某块内存，那么该变量就可以视为该那内存空间中存储的数据值

• 不同数据占用内存空间的大小（事先已经指定好）是不同的

  • 字符型（1字节），整形（4字节），浮点型（8字节）

3.2顺序表

• 集合中存储的元素是有顺序的，顺序表的结构可以分为两种形式：单数据类型和多数据类型。

• python中的列表和元组就属于多数据类型的顺序表

  import numpy as np
  arr = np.array([1,2.2,'three'])
  arr[1]

3.2.1单数据类型顺序表

• 单数据类型顺序表的内存图（内存连续开启）

  

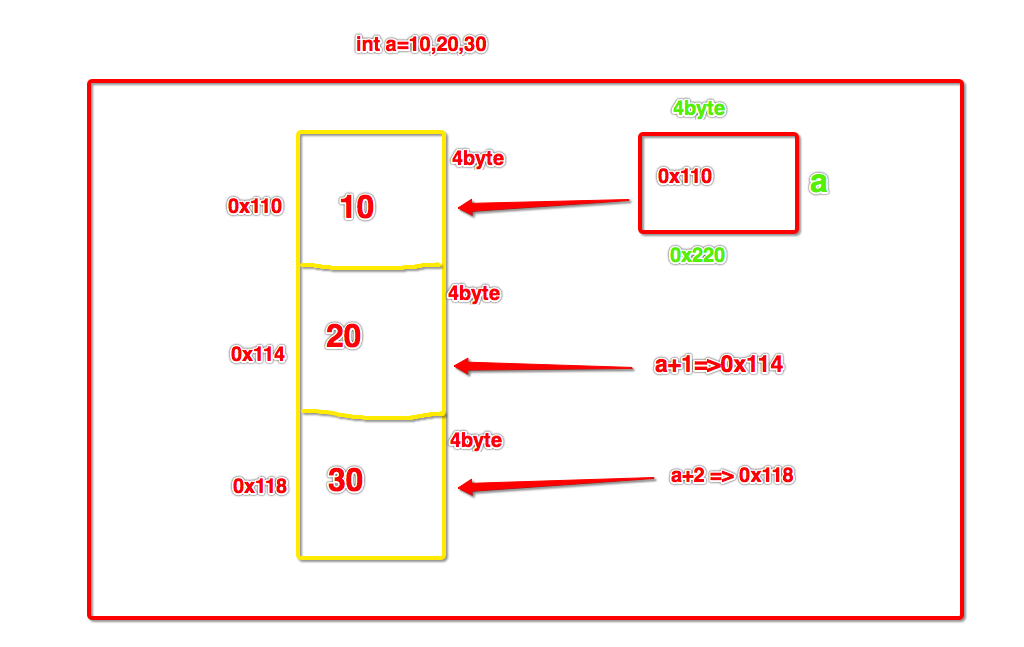
3.2.1多数据类型顺序表

• 多数据类型顺序表的内存图（内存非连续开辟）

  

• 顺序表的弊端：

  • 顺序表的结构需要预先知道数据大小来申请连续的存储空间，而在进行扩充时又需要进行数据的搬迁。

3.3链表

• 链表：相对于顺序表，链表结构可以充分利用计算机内存空间，实现灵活的内存动态管理。

• 链表是通过一个个节点（Node）组成的，每个节点都包含了称为数据域(value)和指针域(next)的基本单元，它也是一种递归的数据结构。它能保持数据之间的逻辑顺序，但存储空间不必按照顺序存储。

  • 链表的节点的结构如下：(data为自定义的数据，next为下一个节点的地址)

  • 链表的结构为，head保存首位节点的地址：

    

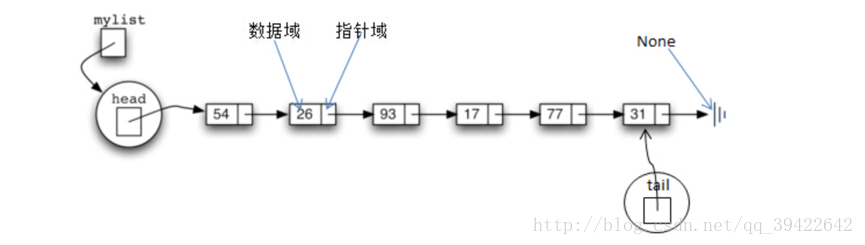
• 链表的基本元素有：

  • 节点：每个节点有两个部分，左边部分称为值域，用来存放用户数据；右边部分称为指针域，用来存放指向下一个元素的指针。

  • head:head节点永远指向第一个节点

  • tail: tail永远指向最后一个节点

  • None:链表中最后一个节点的指针域为None值

• 节点的构建

  class Node():
      def __init__(self,item):
          self.item = item
          self.next = None

3.3.1单链表

• 单向链表也叫单链表，是表中最简单的一种形式，它的每个节点包含两个域，一个信息域（元素域）和一个链接域。这个链接指向链表中的下一个节点，而最后一个节点的链接域则指向一个空值。

  

   

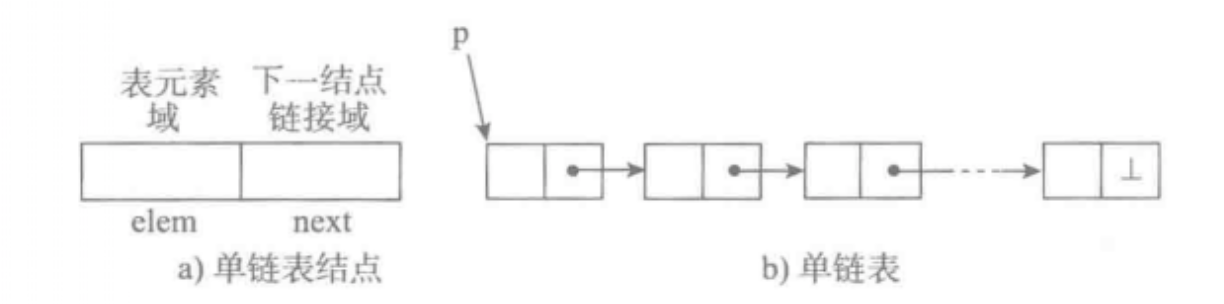
  表中元素elem用来存放具体的数据。链接域next用来存放下一个节点的位置。变量p指向链表的头节点（首节点）的位置，从p出发能找到表中的任意节点。

• 单向链表的抽象数据类型定义:

  • .is_empty()：链表是否为空

  • .length()：链表长度

  • . travel()：遍历整个链表

  • .add(item)：链表头部添加元素

  • .append(item)：链表尾部添加元素

  • . insert(pos, item)：指定位置添加元素

  • .remove(item)：删除节点

  • .search(item)：查找节点是否存在

  class Node():
      def __init__(self,item):
          self.item = item
          self.next = None
  ​
  class Link():
      #构建出一个链表
      def __init__(self):
          self._head = None
      
      #向链表的头部插入节点
      def add(self,item):
          node = Node(item)
          node.next = self._head
          self._head = node
          
      def traver(self):
          cur = self._head
          #如果链表为空,则输出"链表为空"
          if self._head == None:
              print("链表为空")
          while cur:
              print(cur.item)
              cur = cur.next
              
      def isEmpty(self):
          return self._head == None
      
      def length(self):
          cur = self._head
          count = 0
          while cur:
              count += 1
              cur = cur.next
          return count
      
      def search(self,item):
          cur = self._head
          find = False
          while cur:
              if cur.item == item:
                  find = True
                  break
              cur = cur.next
          return find
            
      def append(self,item):
          #构建新节点
          node = Node(item)
          
          if self._head == None:
              self._head = node
              return
              
          cur = self._head  #头结点
          pre = None   #cur的前一个节点
          while cur:
              pre = cur
              cur = cur.next
          pre.next = node
          
      def insert(self,pos,item):
          node = Node(item)
          
          if pos < 0 or pos > self.length():
              print("请重新给pos赋值!!!")
              return
          
          cur = self._head
          pre = None
          for i in range(pos):
              pre = cur
              cur = cur.next
          pre.next = node
          node.next = cur
          
      def remove(self,item):
          cur = self._head
          pre = None
          
          #链表为空
          if self._head == None:
              print("链表为空,无可删除的节点")
              return 
          
          #删除的是第一个节点
          if self._head.item == item:
              self._head = self._head.next
              return
          #删除的是费第一个节点
          while cur:
              pre = cur
              cur = cur.next
              if cur.item == item:
                  pre.next = cur.next
                  return
  ​
          
  link = Link()
  # link.add(3)
  # link.add(4)
  # link.add(5)
  # link.add(6)
  # link.traver()
  # print(link.length())
  # print(link.search(3))
  ​
  link.remove(6)
  # link.append(6)
  # link.insert(7,7)
  link.traver()