一、树
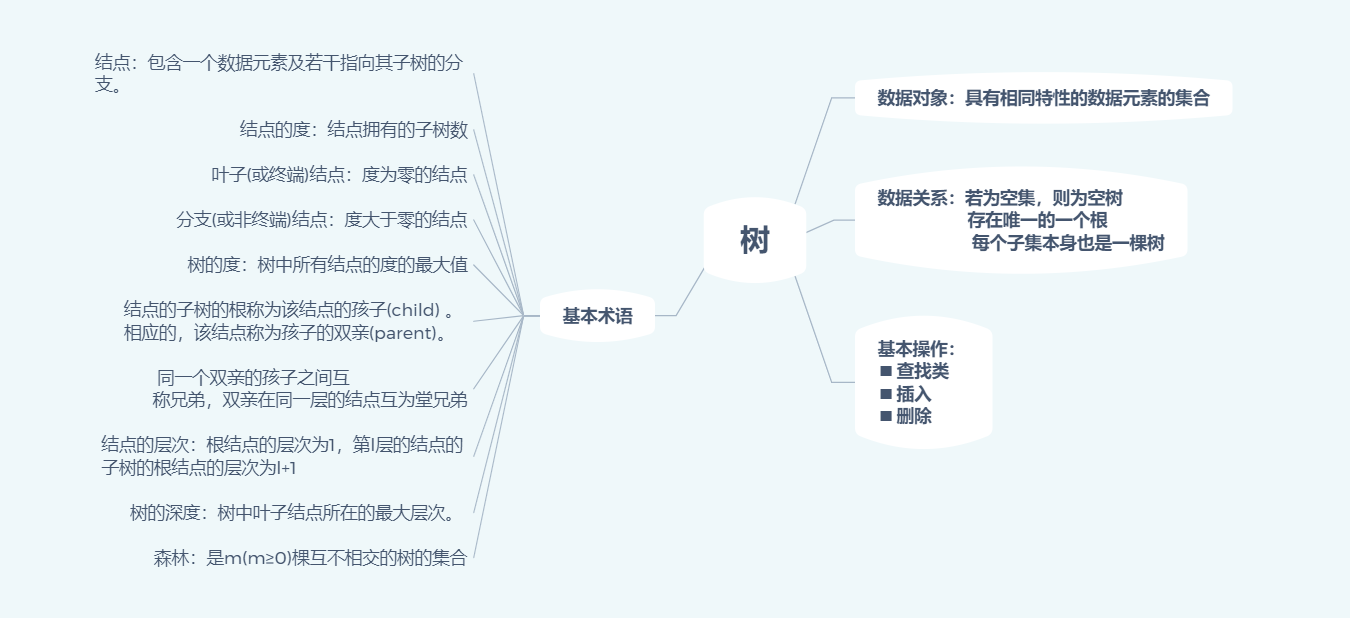
树的基本操作


二、二叉树
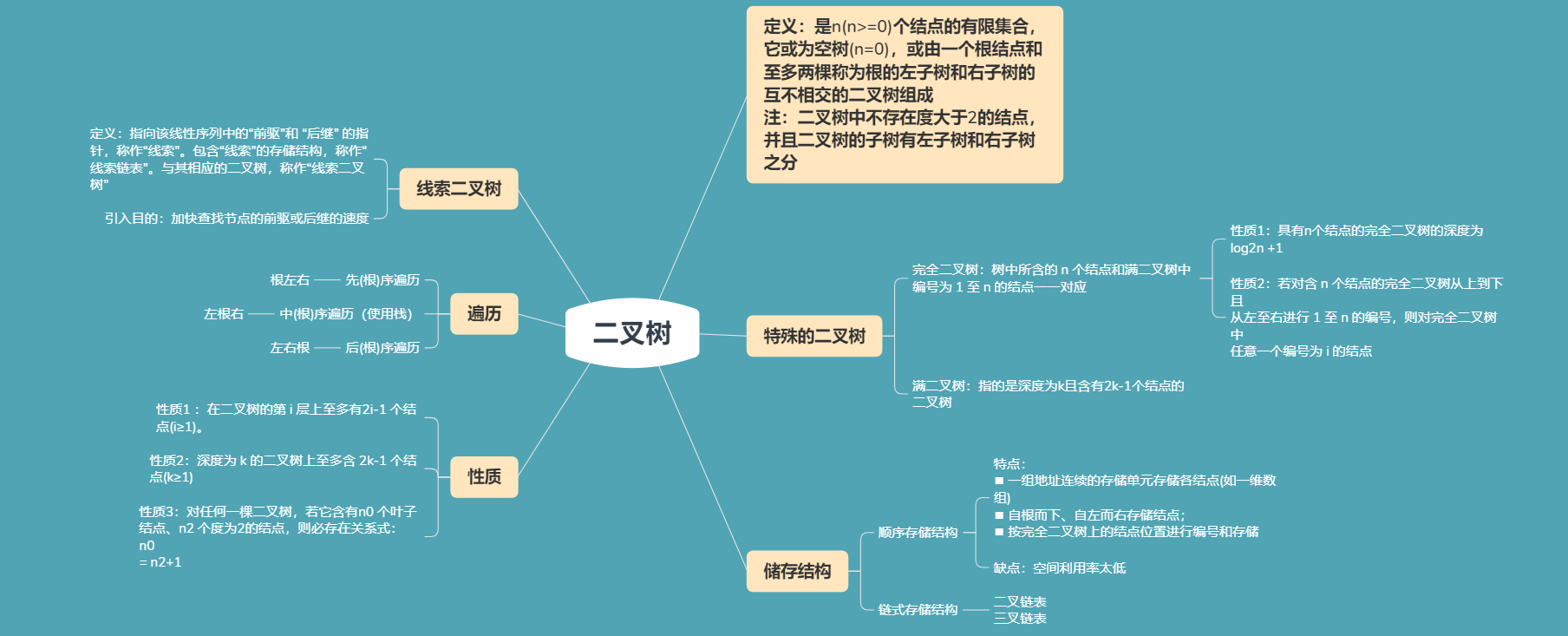
最优二叉树:哈夫曼树
在所有含 n 个叶子结点、并带相同权值的 m 叉树中,必存在一棵其带权路径长度取最小值的树,称为“最优树”
(赫夫曼算法) 以二叉树为例:
⑴根据给定的 n 个权值 {w1, w2, …, wn},构造 n 棵二叉树的集合F = {T1, T2, … , Tn},
其中每棵二叉树中均只含一个带权值为 wi 的根结点,其左、右子树为空树;
⑵在F中选取其根结点的权值最小的两棵二叉树,分别作为左、右子树构造一棵新的二叉树,并置这棵新的二叉树根结点的权值为其左、右子树根结点的权值之和;
⑶从F中删去这两棵树,同时加入刚生成的新树;
⑷重复 (2) 和 (3) 两步,直至 F 中只含一棵树为止。
三、树和森林
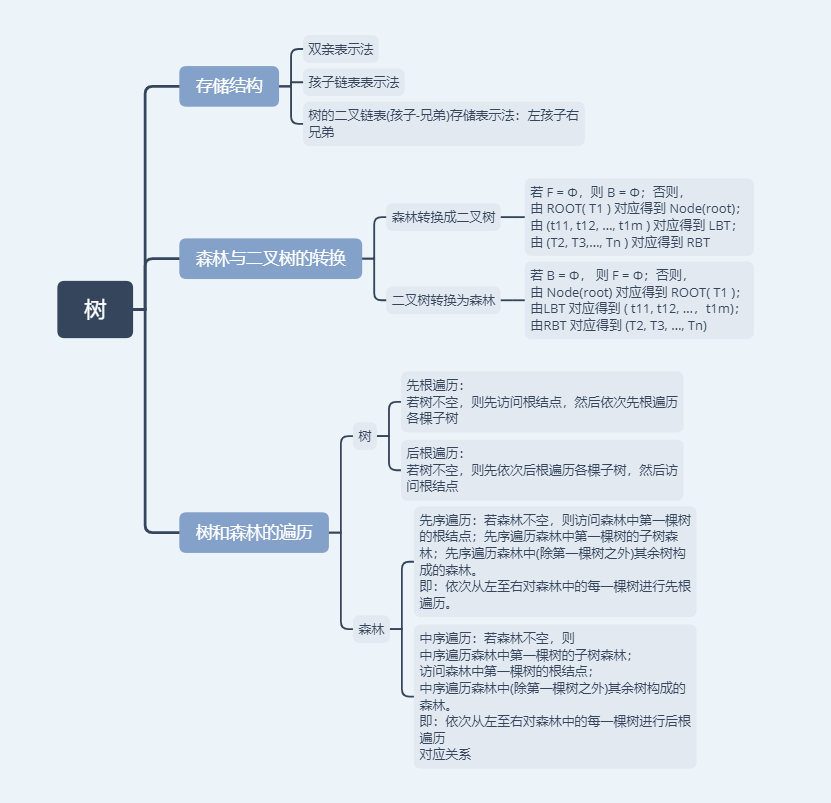
对应关系

四、查找

五、哈希表
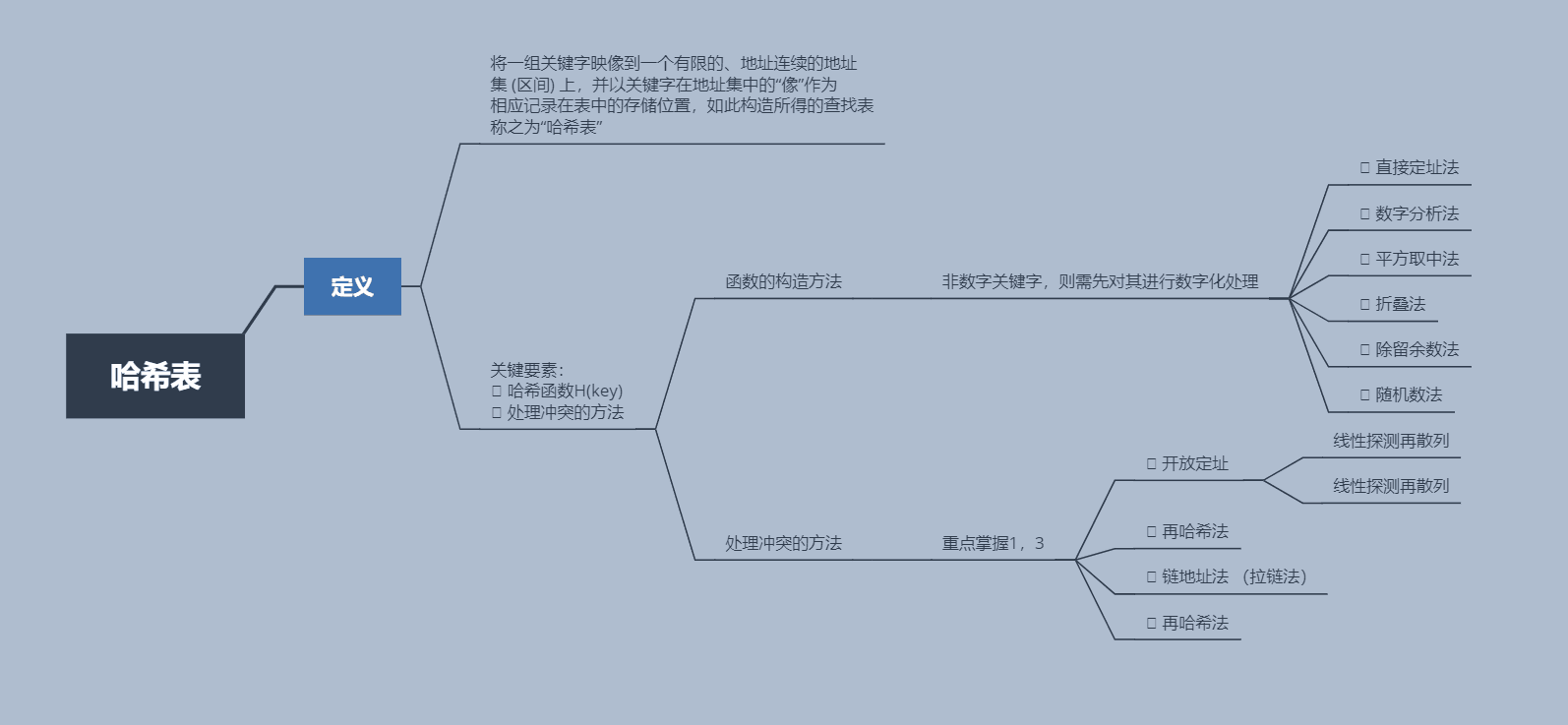
六、疑难问题及解决
树的操作和平衡二叉树的变换,已通过练习和网上的学习资料解决