一、图
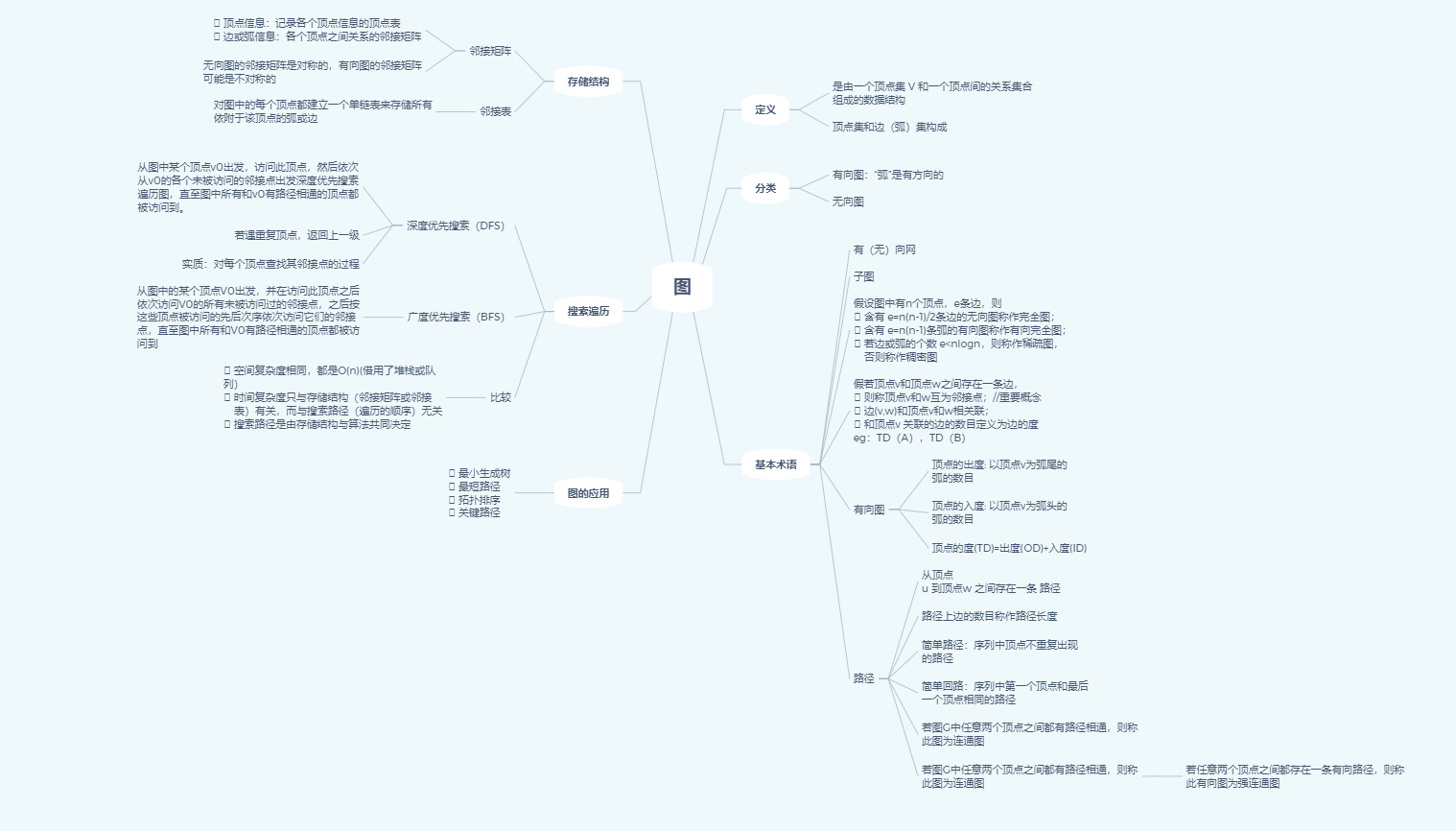
邻接矩阵

邻接表
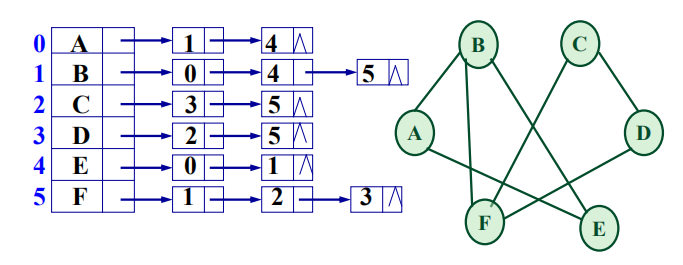
十字链表:查找进入或离开顶点的弧都容易;求顶点的出度和入度方便;建立十字链表时间复杂度与邻接表相同
邻接多重表:同一条边只对应一个边结点,避免数据冗余;建立邻接多重表时间复杂度与邻接表相同,且各种基本操作实现也与邻接表相似
二、图的应用
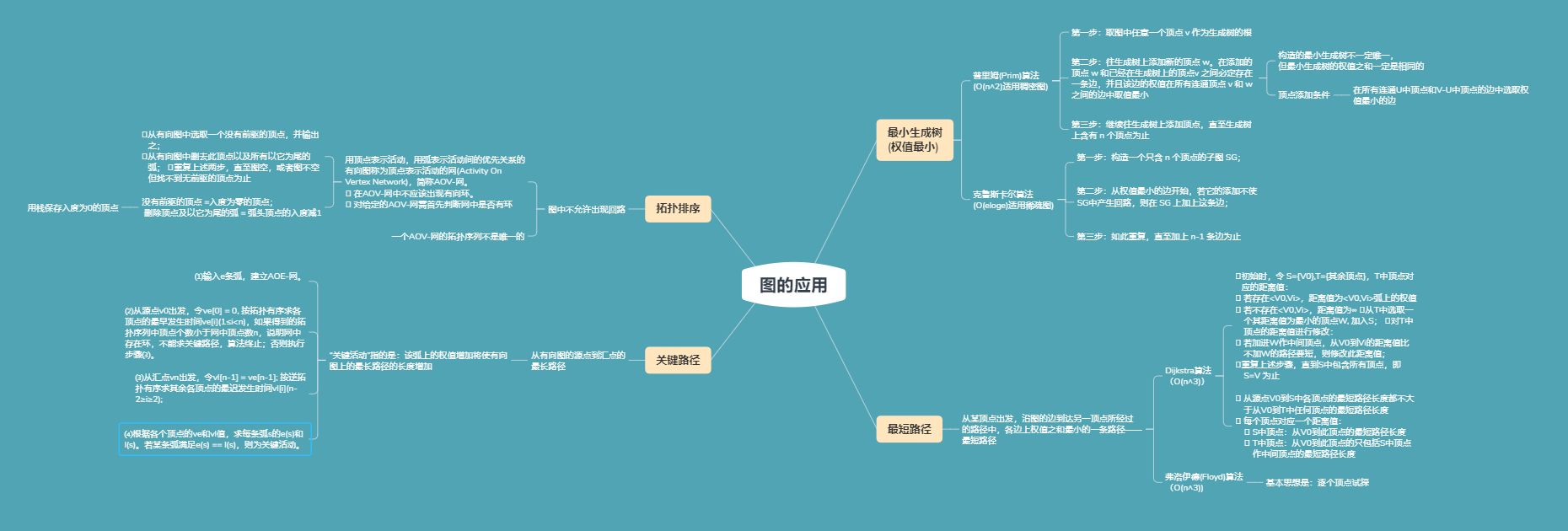
拓扑算法
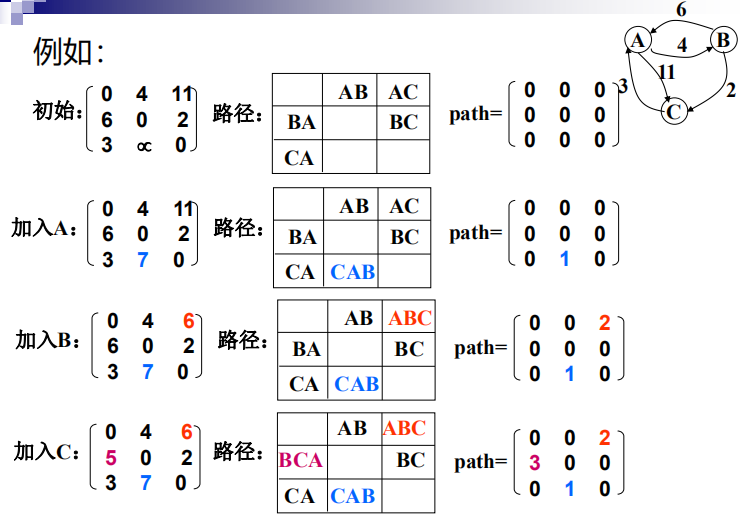
图用邻接矩阵存储;
二维数组c[][]存放最短路径长度;
path[i][j]是从vi到vj的最短路径上vj前一顶点序号。
关键路径符号含义:
事件v**i的最早发生时间:从开始点v1到v**i的最长路径长度。用ve(i)表示。
事件v**i的最迟发生时间:在不推迟整个工期的前提下,事件v**i允许的最晚发生时间。用vl(i)表示。
活动a**i的最早开始时间:即为a**i的弧尾顶点(事件)的最早发生时间。用e(i)表示。
活动a**i的最迟开始时间:在保证不推迟整个工程的完成时间的前提下,活动a**i的最迟开始时间。用 l(i*)表 示。
关键活动:l(i) = e(i)的活动
三、算法伪代码
普里姆(prim)算法
struct {
VertexType adjvex; //U集中的顶点序号
VRType lowcost; //边的权值
} closedge[MAX_VERTEX_NUM];
void MiniSpanTree_P(MGraph G, VertexType u)//用普里姆算法从顶点u出发构造网G的最小生成树
{
k = LocateVex ( G, u );
for (j=0; j<G.vexnum; ++j )//辅助数组初始化
if (j!=k)
closedge[j] = {u,G.arcs[k][j].adj };
closedge[k].lowcost = 0; //初始,U={u}
for (i=0; i<G.vexnum; ++i) {
继续向生成树上添加顶点; }
k = Min(closedge);//求出加入生成树的下一个顶点k
printf(closedge[k].adjvex, G.vexs[k]);
//输出生成树上一条边
closedge[k].lowcost = 0;//第k顶点并入U集
for(j = 0; j < G.vexnum; ++j)
//修改其它顶点的最小边
if (G.arcs[k][j].adj < closedge[j].lowcost)
closedge[j]={G.vexs[k], G.arcs[k][j].adj };
克鲁斯卡尔算法
构造非连通图 ST=( V,{ } );
k = i = 0; // k 计选中的边数
while (k<n-1) {
++i;
检查边集 E 中第 i 条权值最小的边(u,v);
若(u,v)加入ST后不使ST中产生回路,则输出边(u,v);
且k++;
}
Dijkstra算法
void ShortestPath_DIJ(AMGraph G, int v0){
//初始化
n = G.vexnum;
for(v = 0; v<n; ++v){
S[v] = false; //s初始为空集
D[v] = G.arcs[v0][v]; //v0到各个顶点的弧的权值
if (D[v] < MaxInt) Path[v] = v0; //v0和v之间有弧
else Path[v] = -1; //v0和v之间无弧
}
S[v0] = true; //v0加入s
D[v0] = 0; //源点到源点距离为0
.....初始化结束开始进行最短路径求解
for(i = 1;i < n; ++i){
min = MaxInt;
for(w = 0; w < n; ++w){
if(!S[w] && D[w] < min){
v = w; min = D[w];
}//选择一条当前最短路径
}
S[v] = true; //将v加入s
for(w = 0; w < n; ++w)//加入v后,v0到其他节点需更新
if(!S[w] && (D[v] + G.arcs[v][w] < D[w]){
D[w] = D[v] + G.arcs[v][w];
Path[w] = v;
}
}
拓扑排序
取入度为零的顶点v;
while (v<>0) {
printf(v); ++m;
w:=FirstAdj(v);
while (w<>0) {
inDegree[w]--;
w:=nextAdj(v,w);
}
取下一个入度为零的顶点v;
}
if m<n printf(“图中有回路”);
为避免每次都要搜索入度为零的顶点,在算法中设置
一个“栈”,以保存“入度为零”的顶点。
CountInDegree(G,indegree); //对各顶点求入度
InitStack(S);
for ( i=0; i<G.vexnum; ++i)
if (!indegree[i]) Push(S, i); //入度为零的顶点入栈
count=0; //对输出顶点计数
while (!EmptyStack(S)) {
Pop(S, v); ++count; printf(v);
for (w=FirstAdj(v); w; w=NextAdj(G,v,w)){
--indegree(w); // 弧头顶点的入度减一
if(!indegree[w]) Push(S,w);//新产生的入度为零的顶点入栈
}
}
if (count<G.vexnum) printf(“图中有回路”);
四、遇到问题及解决
一开始不能很好的算出最短路径每个顶点的路径长度,现在通过这次整理已经解决