集合
不含任何元素的集合称为空集,记作Ø
元素a属于集合M,记作a∈M.
元素a不属于集合M,记作a∉M
集合的表示法:

(1)列举法:按某种方式列出集合中的全体元素例:有限集合A={a1,a2…,an} ![]()
自然数集N={0,1,2…,n…} ={n}
(2)描述法:M={x | x所具有的特征}
例:整数集合 Z={x l x∈N 或 -x∈N+}
有理数集 Q={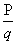 | p∈Z,q∈N+,p与q互质}
| p∈Z,q∈N+,p与q互质}
实数集合 R={x | x为有理数或无理数}

集合之间的关系与运算:
定义设有集合A、B,若x∈A必有x∈B,则称A是B的子集,或称B包含A,或称A包含于B,记作A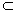 B.
B.
若A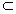 B且B
B且B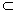 A,则称A与B相等,记作A=B
A,则称A与B相等,记作A=B
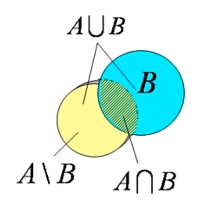
并集 AUB={x|x∈A或x∈B}
交集 A∩B={x|x∈A且x∈B}
差集 AB={x|x∈A且x∉B}
区间与邻域:
区间:是指介于某两个实数之间的全体实数.这两个实数叫做区间的端点.
{x l a<x<b} 称为开区间,记作 (a,b)
![]()
{x l a≤x≤b}称为闭区间,记作[a,b]
![]()
{xla≤x<b}称为半开区间,记作[a,b)
无限区间: [a,+∞)={x|a≤x}
邻域:



映射:
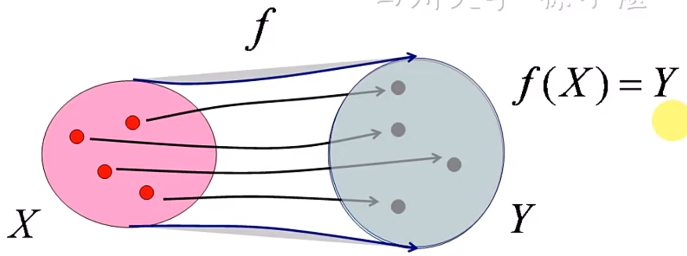
两个非空集合X与Y间存在着对应关系f,而且对于X中的每一个元素x,Y中总有有唯一的一个元素y与它对应,就这种对应称为从X到Y的映射,记作f:X→Y
y称为元素x在映射f下的象,记作:y=f(x)。x称为y关于映射f的原象。集合X中所有元素的象的集合称为映射f的值域,记作f(X)。
满射:Y中的所有元素都是映射f的象
非满射:Y中的部分元素不是映射f的象

单射:X中的不同原象在Y中存在不同的象
单射可以诱导一个逆映射
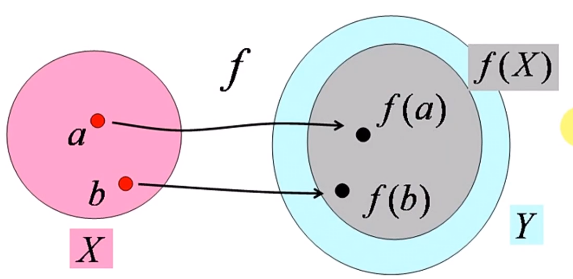
非单射:至少存在两个元素有相同的象
双射(一一映射):即使单射又是满射
函数:
单映射的函数才有反函数
直接函数与反函数是关于y=x对称
符号函数:
y=sgn(x)=
取整函数[向下取整floor]:
y=[x]
![]()
例子
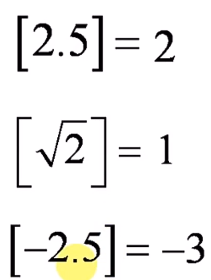
向上取整[ceil]
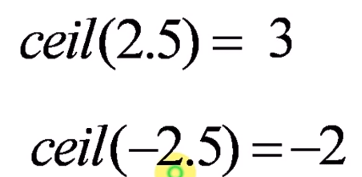
向零取整(trunc---int)-靠近零方向取整:
![]()
![]()
四舍五入函数:
y=round(x)
有界函数:函数在定义域内所对应的所有值域的绝对值都小于等于某个值 |f(x)|<=|M|
如果f(x)>=A 就说f(x)在定义域上有下届,A是下届
如果f(x)<=B 就说f(x)在定义域上有上届,B是上届
有界函数既有上届也有下届;既有上届也有下届的函数肯定是有界函数
单调函数:递增函数或递减函数
偶函数:定义域关于原点对称,f(x)=f(-x)
关于y轴对称
奇函数:定义域关于原点对称,f(x)=-f(x)
关于原点对称
周期函数:
复合函数:
设函数y=f(u)的定义域为Du,值域为Mu,函数u=g(x)的定义域为Dx,值域为Mx,如果Mx∩Du≠Ø,那么对于Mx∩Du内的任意一个x经过u;有唯一确定的y值与之对应,则变量x与y之间通过变量u形成的一种函数关系,这种函数称为复合函数(composite function),记为:y=f[g(x)],其中x称为自变量,u为中间变量,y为因变量(即函数)
y=f(u)称为外函数 u=g(x)称为内函数 u称为中间变量
天子骄龙