矩阵的初等变换

 定义1:三种初等变换：

（i）对换两行（对换 i，j两行，记作 r_i ↔ r_j）；

（ii）以数 k≠0 乘某一行中的所有元（第i行乘 k，记作 r_i×k）；

（iii）把某一行所有元的 k 倍加到另一行对应的元上去（第j 行的 k 倍加到第i行上，记作 r_i +kr_j）

把定义中的“行”换成“列”，即得矩阵的初等列变换的定义（所用记号是把 “r”换成“c”）.

矩阵的初等行变换与初等列变换，统称初等变换

如果矩阵 A 经有限次初等行变换变成矩阵 B，就称矩阵 A 与 B 行等价，记 作 ；如果矩阵 A 经有限次初等列变换变成矩阵 B，就称矩阵 A 与 B 列等 价，记作；如果矩阵A经有限次初等变换变成矩阵B，就称矩阵A与B等价，记作 A ～B.

矩阵之间的等价关系具有下列性质：

（i）反身性 A ～A；

（ii）对称性 若 A～B，则 B～A；

（iii）传递性 若 A ～B，B～C，则 A ～C 

行阶梯形矩阵 

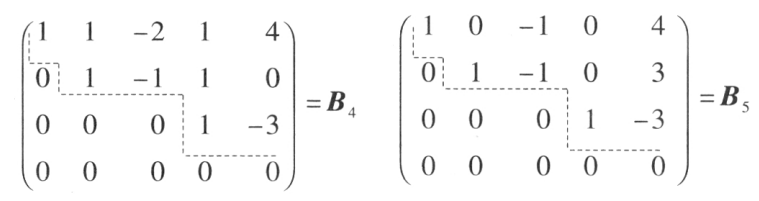
 矩阵 B4 和 B5 的特点是：都可画出一条从第一行某元左方的竖线开始到最 后一列某元下方的横线结束的阶梯线，它的左下方的元全为 0；每段竖线的高度 为一行，竖线的右方的第一个元为非零元，称为该非零行的首非零元.具有这样 特点的矩阵称为行阶梯形矩阵.为明确起见给出如下定义：

定义2 （1）非零矩阵若满足

（i）非零行在零行的上面；

（ii）非零行的首非 零元所在列在上一行（如果存在的话）的首非零元所在列的右面，则称此矩阵为 行阶梯形矩阵

行最简形矩阵

进一步，若 A 是行阶梯形矩阵，并且还满足：（i）非零行的首非零元为 1；（ii）首非零元所在的列的其他元均为 0，则称 A 为行最简形矩阵 

基本的性质