题意:n个人围成一个环,每个人初始有一些金币,每个人可以把金币递给相邻的人,问最少传递多少金币使每个人金币数相同?
分析:首先在保证最优的情况下不可能会出现相邻的两个人互相送金币,因为这样他们公共的部分等于没送,那么我们就可以用bi来表示i号人往左边送的金币,可以为负,为负就表示左边送回来,那么,如果设p为金币相等时每人的金币数(总金币的平均数),ai为i号人原始的金币数,那么很容易得到:
a1-b1+b2=p
a2-b2+b3=p
……
an-bn+b1=p
而我们要求的是bi的绝对值之和,所以再转化一下
b2=p-a1+b1
b3=p-a2+b2
……
bn=p-an+bn-1
然后将所有右试中b2-bn-1代换为b1即
b2=p-a1+b1
b3=p-a2+(p-a1+b1)=p-a1+p-a2+b1
……
bn=p-a1+p-a2+……+p-an-1+b1
而p,a1-an都是常数,输入都给了,所以我们把它写成c使我们看起来方便一些
|b1|=|b1| //这里也可以写成 |b1|=|b1-c1| ,c1=0
|b2|=|b1-c2| ,c2=a1-p
|b3|=|b1-c3| ,c3=a1-p+a2-p
……
|bn|=|b1-cn| ,cn=a1-p+a2-p+……+an-1-p
为什么要写成b1-ci的形式呢?
因为|a-b|相当于在数轴上a与b的距离
所以最终的结果是 |b1| + |b2| + |b3| + …… + |bn| =|b1-c1| + |b2-c2| + …… + |bn-cn|
而只有b1是未知数,所以其实最终结果就是在数轴上离c1,c2,……,cn距离之和的最小值
而这应该初中的时候都学过
将这n个点在数轴上表示出来
这时的c1-cn我将它看做原c数组从小到大排完序后的数组
那么显然为了保证|b1-c1|+|b1-cn|的值最小,b1应该在c1-cn之间
为保证|b1-c2|+|b1-cn-1|的值最小,b1应该在c2-cn-1之间
……
最后如果n是偶数的话,b1取cn/2到cn/2+1之间的值都可以
如果n是奇数的话,b1只能取c(n+1)/2
为了方便我们之间让b1=c(n+1)/2就可以了
这里求c(n+1)/2可以用nth_element() O(n) 有兴趣可以去cplusplus学一下,当然sort也是可以的
最后将b1的值带去原式子中计算就行
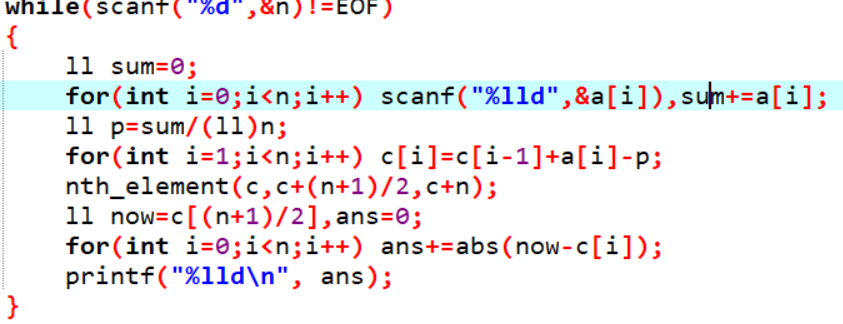
代码: