题意:
给出一棵n个节点的树,这棵树的每条边有一个权值,这个权值只可能是0或1。 在一局游戏开始时,会确定一个节点作为根。接下来从女生开始,双方轮流进行 操作。
当一方操作时,他们需要先选择一个不为根的点,满足该点到其父亲的边权为1; 然后找出这个点到根节点的简单路径,将路径上所有边的权值翻转(即0变成1,1 变成0 )。
当一方无法操作时(即所有边的边权均为0),另一方就获得了胜利。
如果在双方均采用最优策略的情况下,女生会获胜,则输出“Girls win!”,否则输 出“Boys win!”。
为了让游戏更有趣味性,在每局之间可能会有修改边权的操作,而且每局游戏指 定的根节点也可能是不同的。
具体来说,修改边权和进行游戏的操作一共有m个,具体如下:
∙∙“0 x”表示询问对于当前的树,如果以x为根节点开始游戏,哪方会获得胜利。
∙∙“1 x y z ”表示将x和y之间的边的边权修改为z。
分析:
一道在树上的博弈论题
首先,我们先不管是否是最优策略,我们先就愣头青走憨憨走法——每次都走最深的这样一个节点,比如
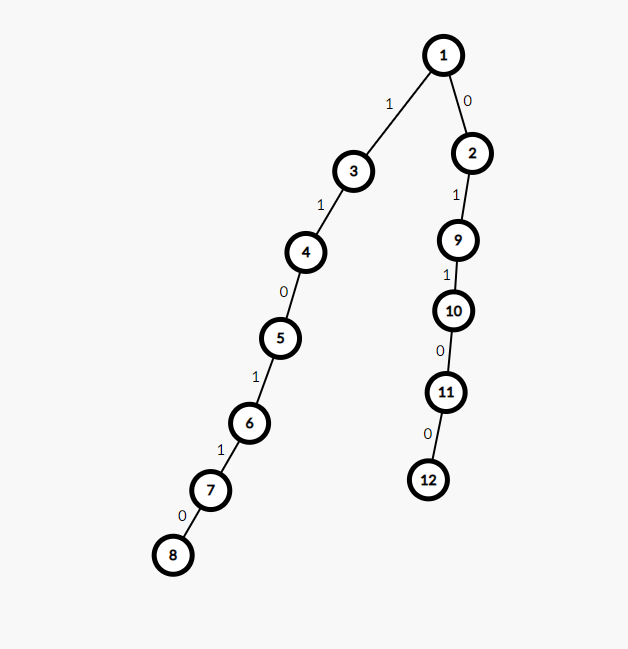
那么我们按照这个规则,先看左边那条链并先选7号节点
对了,这里其实还有一个小小的性质,每条链末尾的0一定是没用的,因为只有他后面的1才能使它翻转成1,而他是末尾的0
所以知道这个性质以及选完7号节点后,树就变成了这样子

然后就是5号节点

最后是4号节点
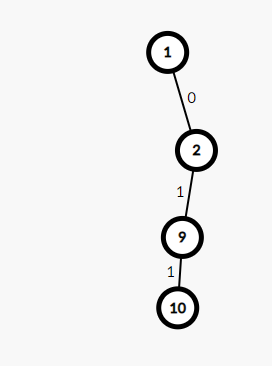
你会发现,假如只有这条链的话到这里已经决出胜负了
而且不难发现的是,在这种憨憨决策中,与根节点直接相连的那条边似乎非常的重要
因为假如我们将这条链划分一下肯定是一块全是1的链,一块全是0的链相间分布(显然)
那么我们这种憨憨走法第一步会将最后一块1的链吞掉,然后剩下的链翻转,你也可以理解为规则翻转,也就是说我们下次就要选0的那块了
以此类推,那么如果最后一块是1的话也就是说连接根节点的那条边是1,那么你就会走奇数步,而如果是0的话就会走偶数步
奇数步与偶数步也就对应了游戏的输赢(奇数对应女孩赢,偶数对应男孩赢)
当然,这种憨憨走法男主和女主显然不会这么走
比如
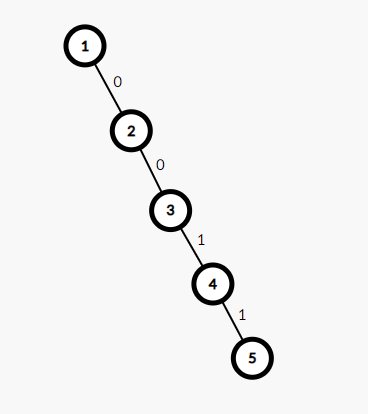
在憨憨走法的前提下,这显然是个男孩必赢的局,那女孩有什么能做的,她可不想输啊!
走5必输,那就走4吧
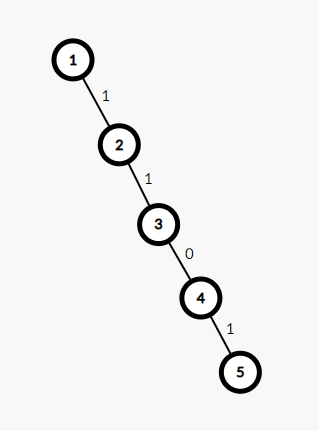
你会发现,之前的走法会让链的块数减一,而这次却让链的块数加一,但这时如果两人继续“憨憨”的话依然是男孩必赢,因为这次相当于男孩先手,而这次有奇数个块,显然男孩必赢
那么我们不难发现,如果我们即使突然“醒悟”,不憨了,但也难逃输的命运,而已经命中注定赢的那位,只需要一直憨下去就行了,当然他也可以皮一下,但就是输不了就很气
当然一条链是这样,更多的链显然也一定是这样,因为每条链都是“命中注定”,那么我们就可以把一颗树化简成一个根节点连着一些节点
因为每条链的结果只与他与根节点连接的那条边有关
原来一条复杂的树,现在只剩下一个“拖把头”,显然就很好做了,轮流取1就完事了,那么很容易得到,最后“拖把头”里1的个数是奇数就是女孩赢,偶数个就是男孩赢
最后就是这个题目中的修改操作以及换根查询了,修改我直接采用莽着改,的确有超时的风险,不过这题核心是想到这个转化,我觉得做数据的应该是做人的qaq
查询当然也是扫一遍他连着的所有边,具体如何实现,我相信你们都写的出来):
代码: