题意:求出{1, 2, 3, 4, 5}的所有满足以 下条件的子集:若 x 在该子集中,则 2x 和 3x 不能在该子集中。(结果对1e9+1取模)
分析:
首先,什么样的数才会产生排斥呢?(选了这个不能选那个) 显然是之比是2或3的啦
其次,很容易想明白的一点就是每个形如1,2,4,8,3,6,9.....这种以一个小的数通过*2*3往外延伸的数列,他们两两之间是互不干扰的
比如,对于从1往外扩展的数列来说可以是1,2,4,8,3,9,27,6,12,24......
他与从5往外扩展的一定是没有交集的,5,10,20,15,30,60……
那么这里自然就很容易想到乘法原理,
也就是说我们解决了每一个这种数列的结果只后只需要乘起来就是最终结果
那么对于每个来说如何解决呢?
首先如果只有之比是2的不能出现在子集中,
第一感觉肯定是“这选相邻的不就完了”
当然,下一秒就会回过神来,显然并不是一眼就能秒出来的(gjk等dalao除外)
这两个题大部分人都过…… 现在大家应该都会迫不及待的打断我“这玩意不就是B题互不侵犯的弱化版吗(甚至弱化到线性)”“这玩意我闭着眼都会打”,
嗯,其实就是用二进制枚举一下这n个2^i里每个位置是否放数,显然如果k&(k>>1)!=0或者k&(k<<1)!=0的话就是不合法的,反之就是合法的
那么现在加一个之比为3的限制又该怎么做呢?
考虑,在没加这个限制之前每个以a为首项的公比为2的数列是互不影响的
而加了这个限制以后这个等比数列里的每一项又与他*3,他*9……扯上了联系
原来是一个一个数(点),加了第一个限制之后变成了一个数列(线)
现在是一个数列(线),再加一个限制,那么变成?
对,变成一个矩阵(面)
所以这也填了开始的坑,为什么要将一个较小数,他*2*3放在一起考虑
而且现在我们知道了,其实开始讲的数列他不是数列而是矩阵,大概长这样
1 2 4 8 16
3 6 12 24 48
9 18 36 72 144
……
而这个又该怎么才能排除掉不合法的呢?
“这不还是B题的弱化版吗”“行了,我会了,再见了您嘞”
没错,这里只需要用状压dp随便搞搞就行,具体的判断条件我相信大家用脚都能打出来,没错就是j&k!=0就不合法,反之合法
最后再梳理一下
首先我们要枚举“最小的数”,这里我用的是判断这个数是否不被2或3整除,
这里类似线性筛,显然如果这个数能被2或3整除,他一定会有一个叫x/2或x/3的来充当“最小的数”
枚举出来最小的数之后,第一列就是x,x*3,x*9,……
然后就是算他每行的列数(x*(3^i)*(2^j)<=n)
最后状压dp随便搞搞就行了
其实这题到这已经基本结束了,但是不知道是不是我菜的原因,又双叒叕t了半天
这边简单介绍几个优化(代码细节)
1.把你单行的判断用一个数组存下状态
比如原来要写for (0 -> 1<<k ) if(k&……)dp[k]……
而现在我们只需要预处理之后 for(0->q.size()) dp[k]……
2.取模->减法

显然减法比取模快不少
3.先用变量代替数组,最后赋值


显然又快不少
4.边干活边赋初值(不用memset,而是在用之前赋初值)



这差的不是一点半点,千万不要一时偷懒调一晚!
最后的最后,再把我关于处理某些细节的代码说一下
1.选出“最小的数”

这里之前说过了
2.计算该行有多少列

这里j是“最小的数”,这里其实应该是以2为底n/j的对数,
我用了个换底公式,好像库里是没有以2为底的函数,只有自然对数和常用对数
具体是为什么这么列式,我觉得真的没啥好说的。。。
3.在何时终止当前行枚举的那层循环

注意,这里的last我有用的,所以最好不要写在循环的第二个分号里(当然这么写再稍微判断一下也是可以的)
4.如何枚举上一层状态,到哪结束
这就是last的意义——记录上一层到q的第多少个,也就是有多少种状态
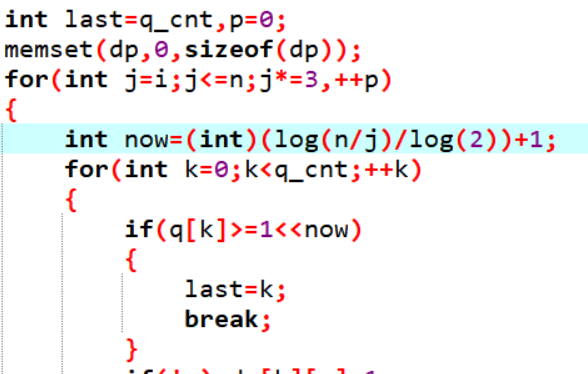
当然这里的last你看我整个循环,其实他是有可能从上面for的第二个分号出去的,所以开始last要赋成q_cnt而不是0,-1之类无意义的值,防止last还没被赋值就跳出来
这次真没了
代码:
#include<cstdio> #include<cmath> using namespace std; #define ll long long const int maxk=2e1+1; const int mod=1e9+1; const int maxn=1e5+1; int dp[maxn][maxk]; int q[maxn]; int pd(int x) { if(x&(x<<1)||x&(x>>1)) return 0; return 1; } int pdd(int x,int y) { if(x&y) return 0; return 1; } int main() { int n; scanf("%d",&n); ll ji=1; int hh=(int)(log(n)/log(2))+1; int q_cnt=0; for(int i=0;i<1<<hh;++i) if(pd(i)) q[q_cnt++]=i; for(int i=1;i<=n;++i) if(i%2&&i%3) { int last=q_cnt,p=0; for(int j=i;j<=n;j*=3,++p) { int now=(int)(log(n/j)/log(2))+1; for(int k=0;k<q_cnt;++k) { if(q[k]>=1<<now) { last=k; break; } if(!p) dp[k][p]=1; else { int nowans=0; for(int t=0;t<last;++t) if(pdd(q[k],q[t])) { nowans+=dp[t][p-1]; if(nowans>=mod) nowans-=mod; } dp[k][p]=nowans; } } } int ans=0; for(int j=0;j<last;++j) { ans+=dp[j][p-1]; if(ans>=mod) ans-=mod; } ji*=(ll)ans,ji%=(ll)mod; } printf("%lld",ji); return 0; }