题意:一棵点数为n的树,每个节点有点权,要求在树中中找到一个最小的x,使得存在一个点满足max(该点点权,该点相邻的点的点权+1,其他点的点权+2)=x
分析:首先要能把题目转化为上述题意
首先题目让你选取一个点为根节点,
然后断掉这个点
让相邻的点与二次相邻的点的点权+1
然后剩下每次只能断掉与该点相邻的点,
断掉后处理与根节点断掉的处理一致
显然,对于任何一个根节点的儿子来说,他的权值一定只被+1
而对于其他节点来说,他的权值一定在他父亲断掉时和爷爷断掉时分别+1,也就是+2
那么我们现在转化完题目,现在剩下的题目其实就是个类似模拟的东西,不过还是有可聊之处的
首先,如果只有一个拥有最大点权的点,令该最大点权为maxa
那么显然一定要以这个节点为根节点,
因为如果不以该节点为根节点,那么最终结果至少为maxa+1
而如果以该节点为根节点,显然当点权为maxa-1的点位于根节点相邻以外的节点时,会使结果变成maxa+1,而且这是最坏情况
最坏情况与最好情况相同,显然要选该节点为根节点
那么求最终结果只需要dfs一下,将根节点的儿子+1,其余节点+2,最后在所有节点中求最大值即可
然后,如果有多个拥有最大点权的点呢?
很容易得到的不一定非要将根节点设在最大点权的点上,比如
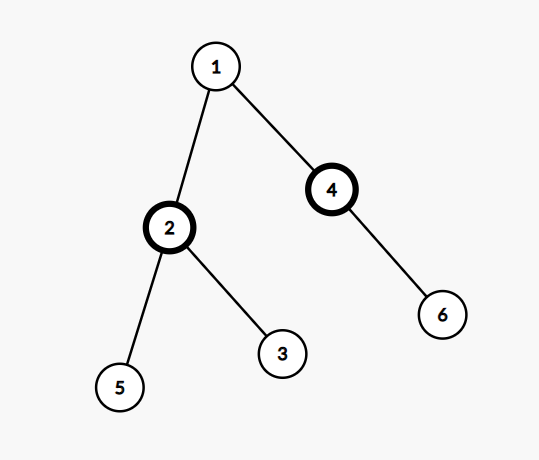
加粗的节点是最大点权的点
显然将根节点设在1一定比将根节点设在2或4更优
那么也很容易得到,当所有的最大点权的点都连在同一个点上时,才会出现maxa+1这种结果,比如
 或
或
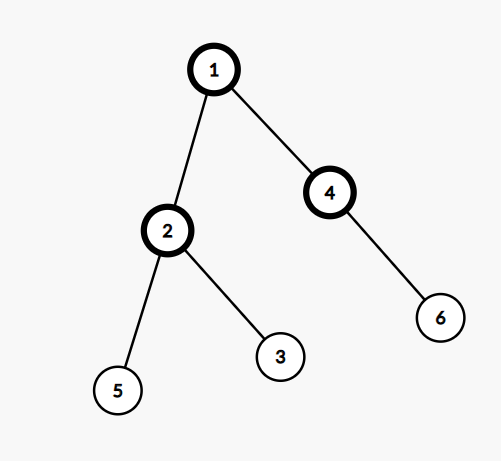
而如果不连在同一个节点上,则结果就是maxa+2,如
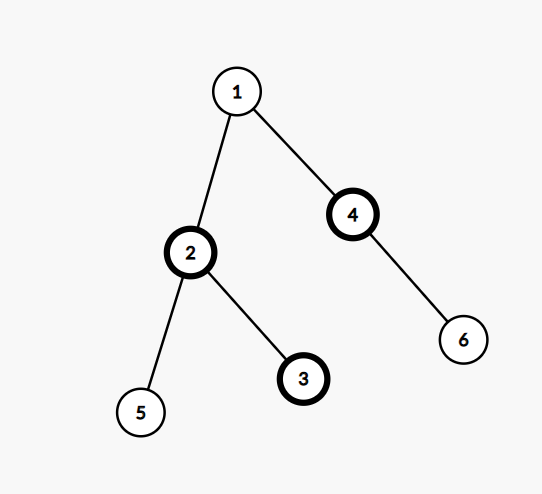
那么我们如何判断所有的最大点权的点是否连在同一个节点上呢?
最简单的方法肯定是直接用floyd之类的方法求出任意两个最大点权的点之间的距离
如果出现有一个距离>2,那么这两个点显然就不可能连在同一个节点上或相邻
如果没有出现,那么显然他们一定是连在同一个节点上的
那么这样的方法显然是超时的,
那么我们能不能省略几次呢?
首先如果我们只以其中任意一个节点为根,
用dfs求出其他节点到该节点的距离,
然后再判断是否存在>2的,
显然并不能得到我们想要的结果,比如
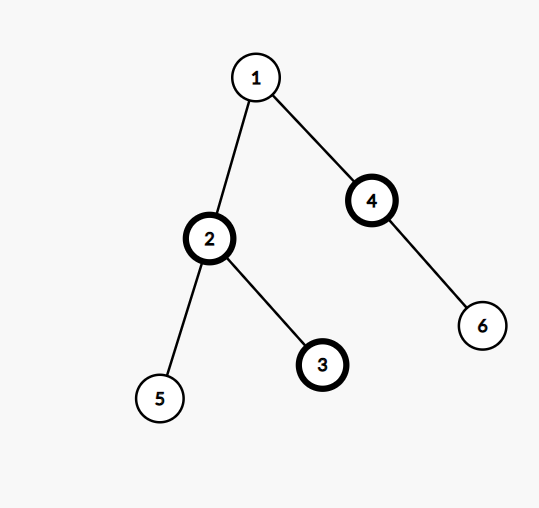
如果我选的是节点2,显然与正确答案不符
那么如果我任选两个可以吗
答案也是不行的,不过这个可能有点难想,比如这个
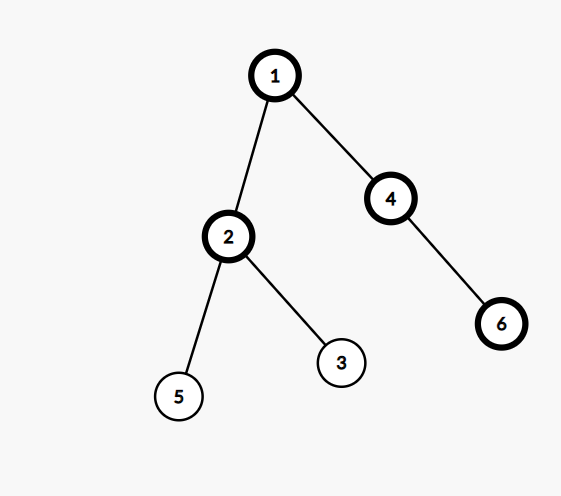
如果我选的是1,4,那么得到的结果就与答案不符
那么如果我选3个呢?
好像没找到反例,那怎么证明一定符合我们的要求呢?
首先,如果存在3个节点没出现距离大于二,那么他们两两之间距离一定小于等于2
那么他们只有两种可能
第一种是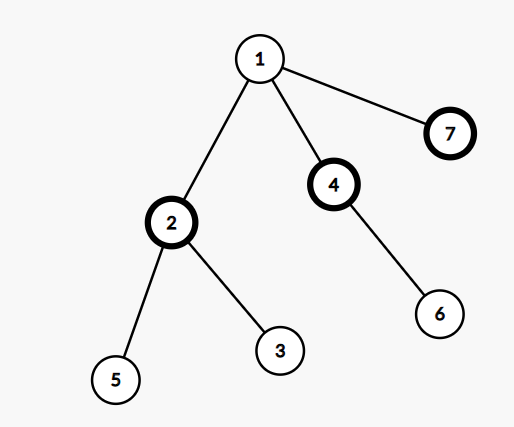
第二种是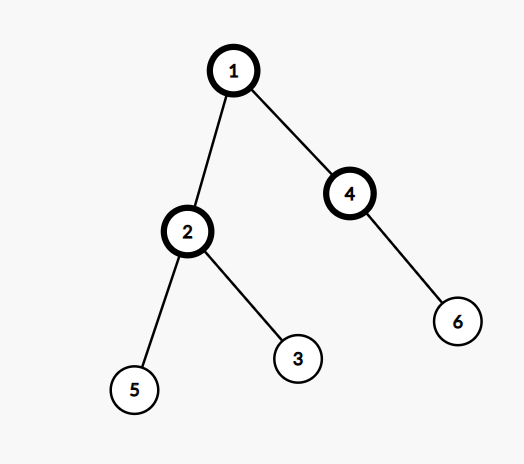
对于第一种来说,其实只需要两个节点保证没有出现距离大于2的节点就可以得到结果
考虑极端的等于2的情况,我对于任意一个根节点一定满足这个图

而此时有两个节点满足该情况,如果出现5,6这种情况,显然就不可能出现两个节点满足该情况
所以也就是说只能出现这种情况

显然这种情况一定是成立的
那么对于第二种情况来说,

4会排除2子树中的干扰,2会排除4子树中的干扰,所以剩余的节点只能为1节点的儿子,从而得证
理一下,刚才较为冗长的证明证明了只需要任选三个最大权值节点dfs即可,这三个节点若找到一个与他们距离>2的最大权值节点,那么最终结果就是maxa+2,否则就是maxa+1
代码:
#include<cstdio> #include<algorithm> #include<vector> using namespace std; const int maxn=3e5+1; const int inf=1e9+1; struct Node { int to,next; }e[maxn<<1]; int head[maxn]; int len[maxn]; int a[maxn]; vector<int> q; int cnt; void add(int x,int y) { e[++cnt].to=y; e[cnt].next=head[x]; head[x]=cnt; } void dfs(int x,int fa) { for(int i=head[x];i;i=e[i].next) { int v=e[i].to; if(v!=fa) { if(fa==-1) a[v]++; else a[v]+=2; dfs(v,x); } } } void dfslen(int x,int fa) { for(int i=head[x];i;i=e[i].next) { int v=e[i].to; if(v!=fa) { len[v]=len[x]+1; dfslen(v,x); } } } int chuli() { for(int i=0;i<min((int)q.size(),3);i++) { len[q[i]]=0; dfslen(q[i],-1); for(int j=0;j<q.size();j++) if(len[q[j]]>2) return 2; } return 1; } int main() { int n,x,y; scanf("%d",&n); int maxa=-inf; for(int i=1;i<=n;i++) { scanf("%d",&a[i]); if(a[i]>maxa) maxa=a[i],q.clear(),q.push_back(i); else if(a[i]==maxa) q.push_back(i); } for(int i=1;i<n;i++) { scanf("%d%d",&x,&y); add(x,y),add(y,x); } if(q.size()==1) { dfs(q[0],-1); for(int i=1;i<=n;i++) maxa=max(maxa,a[i]); printf("%d",maxa); } else printf("%d",maxa+chuli()); return 0; }