题意:有n组数,每组包含两个数,问在每组只能取一个的前提下能组成的最长的从1开始的连续自然数有几个?
分析:刚学了差分约束系统,很容易往转换成图的方向去想
将他读入的这n组数当成边读入
很容易会得到一个图,这个图不一定是连通的,
我们暂时先把他所有极大连通子图划分为两种:一种是 属于树的,另一种是 不属于树的
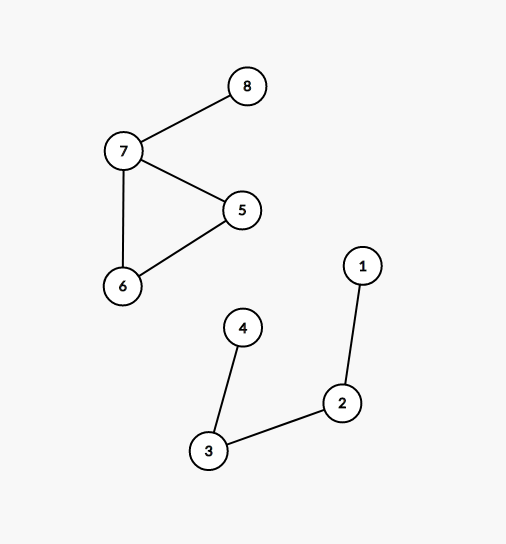
显然,1234是属于树的,而5678则不属于树
对于树来说,显然n个节点的树只能选出n-1个节点来,
这个是很容易证明的,如果我们把不选的那个节点作为根节点,那么显然其他的节点是都可以选的,每个节点只需要用其连向父亲的边即可
再考虑图,其实我们依然可以将每个环缩成点,然后继续考虑缩完点之后剩下的树
首先,对于一颗树来说刚刚已经证明了根节点不选,别的节点都选是最优的
而对于一个环来说一定所有节点都是可以选的,这是显然的
那么如果我将这个环缩成的点作为根,虽然这个环没法在树中被选
但这个环中的每个元素都是被选的
也就是说,只要这个极大连通子图不是树就一定所有节点都能选
而对于树来说,会有一个节点是不能选的,那肯定是让最大的不选是最优的
所以只需要用并查集判断是否是树,如果是树再记录一下最大值即可
代码:
#include<cstdio> #include<cstring> #include<algorithm> using namespace std; const int maxn=1e4+1; int fa[maxn]; int mxp[maxn]; int find(int x) { while(x!=fa[x]) x=fa[x]; return x; } int ya(int x) { int fax=find(x),nowfa; while(x!=fax) { nowfa=fa[x]; fa[x]=fax; x=nowfa; } return fax; } void bing(int x,int y) { int fax=ya(x),fay=ya(y); if(fax==fay) mxp[fax]=maxn; else fa[fay]=fax,mxp[fax]=max(mxp[fax],mxp[fay]); } int main() { int n,x,y; for(int i=1;i<maxn;i++) fa[i]=mxp[i]=i; scanf("%d",&n); while(n--) { scanf("%d%d",&x,&y); bing(x,y); } int ans=maxn; for(int i=1;i<maxn;i++) ya(i); for(int i=1;i<maxn;i++) ans=min(ans,mxp[fa[i]]); printf("%d",ans-1); return 0; }