图论复习O

题意：求p数组分别向右移0~k-1位（最后一个到第一个）时的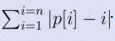值的最小值，并输出最小的k

分析：不难想到要把n²的处理变成线性（也做过很多类似的题了）

显然对于一个值pi来说，他会随着他所处的i的变化，从pi>i变成pi<i

比如，原来是1 3 2 4 5序列，3原来在2号位，3>2，当i增加时，|pi-i|的值变小，也就是序列变成5 1 3 2 4，此时pi（3）已经与i（3）相等了

再移一下位置，序列变成4 5 1 3 2，此时pi（3）已经小于i（4）了，也就是说，再往后移，|pi-i|的值会变大

所以我们需要知道每个pi会在什么时候对结果的贡献从-1变成1，

显然，对于一个数pi>i，他一定会在i'=pi-i时贡献转变，

这里肯定又有人有疑问，那如果这个数循环回开头了呢？

没错

对于当前的i来说，原数组中p[n-i+1]会刚好被换到开头，显然他之前所做的贡献是n-p[n-i+1]，然后转化成了p[n-i+1]-1，

这已经不仅仅是-1变成1的变化了，所以要单独给他把答案加上p[n-i+1]*2-n-1

但此时贡献为-1的个数也变化了，也就是说对于每个i来说，now为当前贡献为-1的数量，now-=b[i-1]-1

其中b[i]表示k=i时贡献从-1变成1的数量，其实就是now要减去k=i-1时发生的贡献转变，再加上末尾跑到开头造成的转变

当然，这个跑到开头的p[n-i+1]也还有再从-1变成1的机会，也就是当前时间i再加上p[n-i+1]-1，也就是在k=p[n-i+1]-1+i时，他会再从-1转成1

最后推导一下当前的结果咋变，

首先，ans要+=p[n-i+1]*2-n-1，当然贡献为-1的有now个，为+1的有n-now个，所以ans还要+=n-now*2，

所以ans+=p[n-i+1]*2-now*2-1？

这就错了，因为答案加上p[n-i+1]*2-n-1的这个-1与now更新时加的一算重了，

所以ans+= p[n-i+1]*2-now*2

代码：

#include<cstdio>
#include<cmath>
using namespace std;

#define ll long long

const int maxn=1e6+1;

int a[maxn];
int b[maxn];

int main()
{
    int n,now;
    ll ans=0;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
        if(a[i]>=i) now++,b[a[i]-i]++;
        ans+=abs(a[i]-i);
    }
    ll minans=ans;
    int p=0;
    for(int i=1;i<=n-1;i++)
    {
        now-=b[i-1]-1;
        if(a[n-i+1]+i<n) b[a[n-i+1]-1+i]++;
        ans+=2ll*(a[n-i+1]-now);
        if(ans<minans) minans=ans,p=i;
    }
    printf("%lld %d",minans,p);
    return 0;
}