Descriptioin
浮生有梦三千场
穷尽千里诗酒荒
徒把理想倾倒
不如早还乡温一壶风尘的酒
独饮往事迢迢
举杯轻思量
泪如潮青丝留他方——乌糟兽/愚青《旧词》
你已经解决了五个问题,不妨在这大树之下,吟唱旧词一首抒怀。最后的问题就是关于这棵树的,它的描述很简单。
给定一棵 (n) 个点的有根树,节点标号 (1 sim n),11 号节点为根。
给定常数 (k) 。
给定 (Q) 个询问,每次询问给定 (x,y)。
求:
(sumlimits_{ileq x} depth(lca(i,y))^k)
(lca(x,y)) 表示节点 (x) 与节点 (y) 在有根树上的最近公共祖先。
(depth(x)) 表示节点 (x) 的深度,根节点的深度为 1。
由于答案可能很大,你只需要输出答案模 998244353 的结果。
Input
输入包含 (n+Q) 行。
第 1 行,三个正整数 (n,Q,k) 。
第 (i=2 sim n) 行,每行有一个正整数 (f_i,(1 leq f_i leq n)),表示编号为 (i) 的节点的父亲节点的编号。
接下来 $ Q$ 行,每行两个正整数 (x,y(1 leq x,y leq n)),表示一次询问。
Output
输出包含 (Q) 行,每行一个整数,表示答案模 998244353 的结果。
Sample Input
5 5 2
1
4
1
2
4 3
5 4
2 5
1 2
3 2
Sample Output
15
11
5
1
6
HINT
样例解释
输入的树:
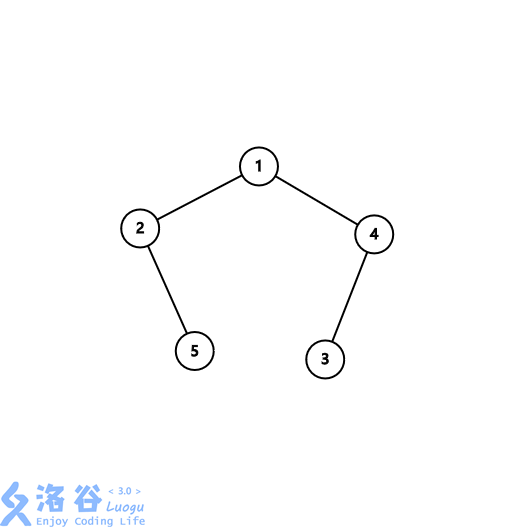
每个点的深度分别为 1,2,3,2,3。
第一个询问 (x = 4,y = 3),容易求出:
(lca(1,3)=1,lca(2,3)=1,lca(3,3)=3,lca(4,3)=4)
于是 (depth(1) +depth(1) +depth(3) +depth(4) =1+1+9+4=15) 。
数据范围 (nleq 50000,mleq 50000,1leq k leq 10^9)
想法
首先一句题外话,我真的很喜欢这种有些文学范儿的题~
言归正传!这个题跟 ([LNOI2014]LCA) 很像,挺套路的。
离线,把所有询问按 (x) 从小到大排序后处理。
考虑当 (k=1) 时,将 (1leadsto [1,x]) 每条路径上经过的点的值都加1,统计 (1leadsto y) 路径上所有点的值之和就是答案
这样做的原理为 对于任意深度为 (i) 的点,它对答案的贡献为 $ i1-(i-1)1=1 $
那么当 (k
eq 1) 时也同理,任意深度为 (i) 的点对答案的贡献为 (i^k-(i-1)^k=c) ,路径上若经过这个点,则该点的值加 (c)
由于所有点深度固定,(k) 也固定, (c) 是很容易处理出来的。
至于如何修改与统计,那当然是树链剖分+线段树咯!(虽说 (lct) 也行,但想想那代码量与极大的常数还是放弃吧 )
代码
#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
int read(){
int x=0;
char ch=getchar();
while(!isdigit(ch)) ch=getchar();
while(isdigit(ch)) x=x*10+ch-'0',ch=getchar();
return x;
}
const int N = 50005;
const int xzy = 998244353;
typedef long long ll;
struct node{
int v;
node *nxt;
}pool[N],*h[N];
int cnt;
void addedge(int u,int v){
node *p=&pool[++cnt];
p->v=v;p->nxt=h[u];h[u]=p;
}
int fa[N],son[N],dep[N],size[N];
void dfs1(int u){
int v,sonnum=0;
size[u]=1;
for(node *p=h[u];p;p=p->nxt){
dep[v=p->v]=dep[u]+1;
dfs1(v);
if(size[v]>sonnum) sonnum=size[v],son[u]=v;
size[u]+=size[v];
}
}
int top[N],w[N],rk[N],tot;
void dfs2(int u){
int v=son[u];
if(v){
top[v]=top[u];
w[v]=++tot;
rk[tot]=v;
dfs2(v);
}
for(node *p=h[u];p;p=p->nxt)
if((v=p->v)!=son[u]){
top[v]=v;
w[v]=++tot;
rk[tot]=v;
dfs2(v);
}
}
int n,m,k;
int Pow_mod(int x,int y){
int ret=1;
while(y){
if(y&1) ret=((ll)ret*x)%xzy;
x=((ll)x*x)%xzy;
y>>=1;
}
return ret;
}
struct tree{
tree *ch[2];
int e,sum,lazy;
}pool2[N*2],*root;
int cnt2;
void build(tree *p,int l,int r){
p->sum=p->lazy=0;
if(l==r){
p->e=(Pow_mod(dep[rk[l]],k)-Pow_mod(dep[rk[l]]-1,k)+xzy)%xzy;
return;
}
int mid=(l+r)>>1;
build(p->ch[0]=&pool2[++cnt2],l,mid);
build(p->ch[1]=&pool2[++cnt2],mid+1,r);
p->e=((ll)p->ch[0]->e+p->ch[1]->e)%xzy;
}
void update(tree *p) { p->sum=((ll)p->ch[0]->sum+p->ch[1]->sum)%xzy; }
void pushdown(tree *p){
if(!p->lazy) return;
for(int i=0;i<2;i++){
(p->ch[i]->lazy+=p->lazy)%=xzy;
p->ch[i]->sum=((ll)p->ch[i]->sum+1ll*p->lazy*p->ch[i]->e%xzy)%xzy;
}
p->lazy=0;
}
void change(tree *p,int l,int r,int L,int R){
if(l==L && r==R){
p->lazy++;
p->sum=(p->sum+p->e)%xzy;
return;
}
pushdown(p);
int mid=(l+r)>>1;
if(R<=mid) change(p->ch[0],l,mid,L,R);
else if(L>mid) change(p->ch[1],mid+1,r,L,R);
else{
change(p->ch[0],l,mid,L,mid);
change(p->ch[1],mid+1,r,mid+1,R);
}
update(p);
}
int query(tree *p,int l,int r,int L,int R){
if(l==L && r==R) return p->sum;
pushdown(p);
int mid=(l+r)>>1;
if(R<=mid) return query(p->ch[0],l,mid,L,R);
else if(L>mid) return query(p->ch[1],mid+1,r,L,R);
return (query(p->ch[0],l,mid,L,mid)+query(p->ch[1],mid+1,r,mid+1,R))%xzy;
}
void add(int x){
while(x){
change(root,1,n,w[top[x]],w[x]);
x=fa[top[x]];
}
}
int ask(int x){
int ret=0;
while(x){
(ret+=query(root,1,n,w[top[x]],w[x]))%=xzy;
x=fa[top[x]];
}
return ret;
}
struct data{
int x,y,id;
bool operator < (const data &b) const{ return x<b.x; }
}d[N];
int ans[N];
int main()
{
n=read(); m=read(); k=read();
for(int i=2;i<=n;i++) {
fa[i]=read();
addedge(fa[i],i);
}
for(int i=0;i<m;i++) {
d[i].x=read(); d[i].y=read();
d[i].id=i;
}
sort(d,d+m);
dep[1]=1;
dfs1(1);
top[1]=1; w[1]=++tot; rk[tot]=1;
dfs2(1);
build(root=&pool2[++cnt2],1,n);
int t=0;
for(int i=0;i<m;i++){
while(t<d[i].x) add(++t);
ans[d[i].id]=ask(d[i].y);
}
for(int i=0;i<m;i++) printf("%d
",ans[i]);
return 0;
}