Description
在列奥纳多·达·芬奇时期,有一个流行的童年游戏,叫做“连珠线”。不出所料,玩这个游戏只需要珠子和线,珠子从1到礼编号,线分为红色和蓝色。游戏
开始时,只有1个珠子,而接下来新的珠子只能通过线由以下两种方式被加入:
1.Append(w,杪):-个新的珠子w和一个已有的珠子杪连接,连接使用红线。
2.Insert(w,u,v):-个新的珠子w加入到一对通过红线连接的珠子(u,杪)
之间,并将红线改成蓝线。也就是将原来u连到1的红线变为u连到w的蓝线与W连到V的蓝线。
无论红线还是蓝线,每条线都有一个长度。而在游戏的最后,将得到游戏的
最后得分:所有蓝线的长度总和。
现在有一个这个游戏的最终结构:你将获取到所有珠子之间的连接情况和所
有连线的长度,但是你并不知道每条线的颜色是什么。
你现在需要找到这个结构下的最大得分,也就是说:你需要给每条线一个颜
色f红色或蓝色),使得这种连线的配色方案是可以通过上述提到的两种连线方式
操作得到的,并且游戏得分最大。在本题中你只需要输出最大的得分即可。
Input
第一行是一个正整数n,表示珠子的个数,珠子编号为1刭n。
接下来n-l行,每行三个正整数ai,bi(l≤ai10000),表示有一条长度为ci的线连接了珠子ai和珠子bi。
Output
输出一个整数,为游戏的最大得分。
Sample Input
1 2 10
1 3 40
1 4 15
1 5 20
Sample Output
HINT
数据范围满足1≤n≤200000。
题解:
看到这道题,可以从两个角度入手考虑:
1)对于这棵树最终的形态,考虑哪些边可能是蓝边,并计算最大值
2)考虑这棵树建树的过程。在一开始只有根节点,后来不断加点过程中有哪些边是蓝边,并计算最大值
我一开始是从第一个角度考虑的
通过手动根据样例画图发现,蓝边一定是两条两条地连在一起(因为每次Insert操作都是两边一起变蓝,且这两边是相邻的)
考虑这两条蓝边(指同时出现的那两条蓝边)可能的连法:
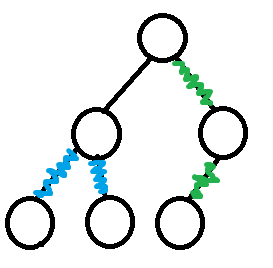
连法一如两条蓝色边所示,连法二如两条绿色边所示
一个点若是两条蓝边的中心点,那两条蓝边要么是与自己两个孩子的连边,要么是与自己一个孩子的连边加上自己与父节点的连边
然后就可以树形dp了
f[0][i]表示i号点不做两条蓝边中心点:
f[0][i]=它每一个son可得到的最大值 的和
f[1][i]表示i号点做两条蓝边中心点,且是连法一:
f[1][i]=(选两个son,每个son不向i连边可得最大值 的和)+(这两个son到点i边的长度)+(其他son可得到的最大值 的和)
f[2][i]表示i号点做两条蓝边中心点,是连法二:
f[2][i]=(选一个son,该son不向i连边可得到的最大值)+(这个son到点i边的长度)+(点i到父节点边的长度)+(其他son可得到的最大值 的和)
大体思路就是这样,看起来很对吧……
然而是有问题的!我一开始就以为这样是对的,但发现WA,洛谷上也只得了20分……
一组反例:
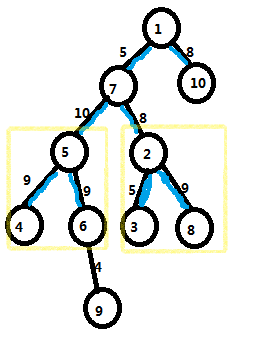
按照上面的算法,最大值时蓝边应这么连
但注意两个黄框
必须先存在4、6才能出现5,必须先存在3、8才能出现2
对于7,必须2、5都存在且连上了一条边才可以出现
假设先以9-4-6-5的顺序把5及其子树都出现了,要想再出现2,需要让3、8出现
但3、8都是叶节点,唯一与2的连边还是蓝边,说明他们只能是一开始连了一条边,之后插入2
但这时5及其子树已插入完了,3、8没有与已存在的这棵树连在一起
2想出现的话只能3、8单成一棵树,与题目不符!
为了保证符合题意,我们考虑第二个角度
假设已确定根节点了,那么由题意,所有“两条蓝边”都是上面所说的连法二,不可能为连法一
这样同样可以树形dp,而且比上面的还简单
(转移方法与上面类似,不详细说了)
但是这是在确定一个根节点的情况下,而每个点都可能是根节点。
暴力每次树形dp的话O(n²)伤不起……
于是考虑换根。
从上到下换根。每次选当前“根节点”的一个未当过根的子节点作为新的根节点,把当前这个点作为它的子节点,O(1)维护各种信息
这样就很快了,只是细节需要多多多多多多注意一下
代码:
(注:为了方便计算,我多用了几个数组计算不同的东西,细节有点多)

1 #include<cstdio> 2 #include<iostream> 3 #include<algorithm> 4 #define INF 2100000000 5 using namespace std; 6 7 const int N = 200005; 8 int f[4][N],ma[N][2]; 9 10 struct node{ 11 int v,len; 12 node *next; 13 }pool[2*N],*h[N]; 14 int cnt; 15 void addedge(int u,int v,int len){ 16 node *p=&pool[++cnt],*q=&pool[++cnt]; 17 p->v=v;p->next=h[u];h[u]=p;p->len=len; 18 q->v=u;q->next=h[v];h[v]=q;q->len=len; 19 } 20 21 int fa[N],dis[N]; 22 int n; 23 void dfs(int u){ 24 int v,num1=-INF,num2=-INF,m1=0,m2=0; 25 f[0][u]=f[1][u]=f[2][u]=f[3][u]=0; 26 for(node *p=h[u];p;p=p->next) 27 if(!fa[v=p->v]){ 28 fa[v]=u; 29 dis[v]=p->len; 30 dfs(v); 31 f[0][u]+=f[2][v]; 32 if(f[3][v]>num1) num2=num1,m2=m1,num1=f[3][v],m1=v; 33 else if(f[3][v]>num2) num2=f[3][v],m2=v; 34 } 35 if(m1) f[1][u]=dis[u]+num1+f[0][u]; 36 ma[u][0]=m1;ma[u][1]=m2; 37 f[2][u]=max(f[1][u],f[0][u]); 38 f[3][u]=f[0][u]-f[2][u]+dis[u]; 39 } 40 41 int ans=0; 42 void dfs2(int u){ 43 int v; 44 int pre[4],mm[2],ff,d; 45 for(int i=0;i<4;i++) pre[i]=f[i][u]; 46 d=dis[u]; 47 48 ans=max(ans,f[0][u]); 49 for(node *p=h[u];p;p=p->next) 50 if(fa[v=p->v]==u){ 51 f[0][u]=f[0][u]-f[2][v]; 52 dis[u]=p->len; 53 if(ma[u][0]==v) 54 if(ma[u][1]) f[1][u]=f[0][u]+f[3][ma[u][1]]+dis[u]; 55 else f[1][u]=0;/**/ 56 else if(ma[u][0]) 57 f[1][u]=f[0][u]+f[3][ma[u][0]]+dis[u]; 58 f[2][u]=max(f[1][u],f[0][u]); 59 f[3][u]=f[0][u]-f[2][u]+dis[u]; 60 mm[0]=ma[v][0];mm[1]=ma[v][1]; 61 if((mm[0] && f[3][u]>f[3][mm[0]]) || !mm[0]) ma[v][1]=ma[v][0],ma[v][0]=u; 62 else if((mm[1] && f[3][u]>f[3][mm[1]]) || !mm[1]) ma[v][1]=u; 63 64 ff=f[0][v]; 65 f[0][v]+=f[2][u]; 66 67 dfs2(v); 68 69 for(int i=0;i<4;i++) f[i][u]=pre[i]; 70 dis[u]=d;f[0][v]=ff; 71 ma[v][0]=mm[0];ma[v][1]=mm[1]; 72 } 73 } 74 75 int main() 76 { 77 int i,a,b,c; 78 scanf("%d",&n); 79 for(i=1;i<n;i++) 80 scanf("%d%d%d",&a,&b,&c),addedge(a,b,c); 81 82 fa[1]=-1;dis[1]=0; 83 dfs(1); 84 dfs2(1); 85 86 printf("%d ",ans); 87 88 return 0; 89 }
