Description###
windy在有向图中迷路了。 该有向图有 N 个节点,windy从节点 0 出发,他必须恰好在 T 时刻到达节点 N-1。 现在给出该有向图,你能告诉windy总共有多少种不同的路径吗? 注意:windy不能在某个节点逗留,且通过某有向边的时间严格为给定的时间。
Input###
第一行包含两个整数,N T。 接下来有 N 行,每行一个长度为 N 的字符串。 第i行第j列为'0'表示从节点i到节点j没有边。 为'1'到'9'表示从节点i到节点j需要耗费的时间。
Output###
包含一个整数,可能的路径数,这个数可能很大,只需输出这个数除以2009的余数。
Sample Input###
【输入样例一】
2 2
11
00
【输入样例二】
5 30
12045
07105
47805
12024
12345
Sample Output###
【输出样例一】
1
【样例解释一】
0->0->1
【输出样例二】
852
HINT###
30%的数据,满足 2 <= N <= 5 ; 1 <= T <= 30 。 100%的数据,满足 2 <= N <= 10 ; 1 <= T <= 1000000000 。
想法##
dp方程还是很显然的,设 (f[i][j]) 表示在第i时刻到达点j的方案数
$f[i][j]=sumlimits_{e[k][i]
eq 0} f[j-e[k][i]][k] $ ((e[i][j])为结点i到结点j花费的时间)
然而T这么大肯定是过不了的。
这时注意到n很小,像这种变量一大一小的果断矩阵乘法。
由于(e[i][j] leq 9) , 所以计算某一时间时只会用到前9个时间。
不同于“计算斐波那契数列”那种基本的矩阵乘法,这里的f不是一维的,而是二维的。
但没关系,由于会用到的f值比较少,所以可以把二维强行拉成一维。
像这样:
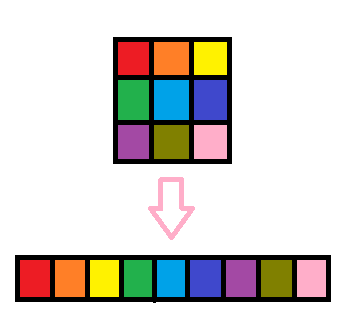
然后就像普通的矩阵乘法一样搞就好了。
代码##
细节有点多,要想清楚一些。
P.S. 代码中的转移并不是上面所说的那种,而是用(f[i][j])更新(f[i+e[j][k]][k]),这样写起来更方便。
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#define P 2009
using namespace std;
const int SZ = 100;
struct matrix{
int a[SZ][SZ];
matrix() { memset(a,0,sizeof(a)); }
void init() { for(int i=0;i<SZ;i++) a[i][i]=1; }
matrix operator * (matrix &b) const{
matrix c;
for(int i=0;i<SZ;i++)
for(int j=0;j<SZ;j++)
for(int k=0;k<SZ;k++)
(c.a[i][j]+=a[i][k]*b.a[k][j])%=P;
return c;
}
matrix operator *= (matrix &b) { return *this=*this*b; }
};
matrix Pow_mod(matrix x,int y){
matrix ret; ret.init();
while(y){
if(y&1) ret*=x;
x*=x;
y>>=1;
}
return ret;
}
int n,T;
char e[15][15];
int main()
{
scanf("%d%d",&n,&T);
for(int i=1;i<=n;i++)
scanf("%s",e[i]+1);
matrix a,b;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(e[i][j]!='0') {
a.a[(i-1)*9][(j-1)*9+e[i][j]-'0'-1]++;
}
for(int i=1;i<=n;i++)
for(int j=0;j<8;j++) a.a[(i-1)*9+j+1][(i-1)*9+j]++;
b.a[0][0]=1;
a=Pow_mod(a,T);
b*=a;
printf("%d
",b.a[0][(n-1)*9]);
return 0;
}