《用Python玩转数据》项目—线性回归分析入门之波士顿房价预测（二）

接上一部分，此篇将用tensorflow建立神经网络，对波士顿房价数据进行简单建模预测。

二、使用tensorflow拟合boston房价datasets

1、数据处理依然利用sklearn来分训练集和测试集。

2、使用一层隐藏层的简单网络，试下来用当前这组超参数收敛较快，准确率也可以。

3、激活函数使用relu来引入非线性因子。

4、原本想使用如下方式来动态更新lr，但是尝试下来效果不明显，就索性不要了。

def learning_rate(epoch):
    if epoch < 200:
        return 0.01
    if epoch < 400:
        return 0.001
    if epoch < 800:
        return 1e-4

 好了，废话不多说了，看代码如下：

from sklearn import datasets
from sklearn.model_selection import train_test_split
import os
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf

dataset = datasets.load_boston()
x = dataset.data
target = dataset.target
y = np.reshape(target,(len(target), 1))

x_train, x_verify, y_train, y_verify = train_test_split(x, y, random_state=1)
y_train = y_train.reshape(-1)
train_data = np.insert(x_train, 0, values=y_train, axis=1)


def r_square(y_verify, y_pred):
    var = np.var(y_verify)
    mse = np.sum(np.power((y_verify-y_pred.reshape(-1,1)), 2))/len(y_verify)
    res = 1 - mse/var
    print('var:', var)
    print('MSE-ljj:', mse)
    print('R2-ljj：', res)


EPOCH = 3000
lr = tf.placeholder(tf.float32, [], 'lr')
x = tf.placeholder(tf.float32, shape=[None, 13], name='input_feature_x')
y = tf.placeholder(tf.float32, shape=[None, 1], name='input_feature_y')

W = tf.Variable(tf.truncated_normal(shape=[13, 10], stddev=0.1))
b = tf.Variable(tf.constant(0., shape=[10]))

W2 = tf.Variable(tf.truncated_normal(shape=[10, 1], stddev=0.1))
b2 = tf.Variable(tf.constant(0., shape=[1]))


with tf.Session() as sess:
    hidden1 = tf.nn.relu(tf.add(tf.matmul(x, W), b))

    y_predict = tf.add(tf.matmul(hidden1, W2), b2)
    loss = tf.reduce_mean(tf.reduce_sum(tf.pow(y-y_predict,2), reduction_indices=[1]))
    print(loss.shape)
    train = tf.train.AdamOptimizer(learning_rate=lr).minimize(loss)

    sess.run(tf.global_variables_initializer())
    saver = tf.train.Saver()
    W_res = 0
    b_res = 0
    try:
        last_chk_path = tf.train.latest_checkpoint(checkpoint_dir='/home/ljj/PycharmProjects/mooc/train_record')
        saver.restore(sess, save_path=last_chk_path)
    except:
        print('no save file to recover-----------start new train instead--------')

        loss_list = []
        over_flag = 0
        for i in range(EPOCH):
            if over_flag ==1:
                    break
            y_t = train_data[:, 0].reshape(-1, 1)
            _, W_res, b_res, loss_train = sess.run([train, W, b, loss],
                                                   feed_dict={x: train_data[:, 1:],
                                                              y: y_t,
                                                              lr: 0.01})

            checkpoint_file = os.path.join('/home/ljj/PycharmProjects/mooc/train_record', 'checkpoint')
            saver.save(sess, checkpoint_file, global_step=i)
            loss_list.append(loss_train)
            if loss_train < 0.2:
                over_flag = 1
                break
            if i %500 == 0:
                print('EPOCH = {:}, train_loss ={:}'.format(i, loss_train))
            if i % 500 == 0:
                r = loss.eval(session=sess, feed_dict={x: x_verify,
                                                       y: y_verify,
                                                       lr: 0.01})
                print('verify_loss = ',r)
            np.random.shuffle(train_data)

        plt.plot(range(len(loss_list)-1), loss_list[1:], 'r')
        plt.show()

    print('final loss = ',loss.eval(session=sess, feed_dict={x: x_verify,
                                           y: y_verify,
                                           lr: 0.01}))

    y_pred = sess.run(y_predict, feed_dict={x: x_verify,
                                           y: y_verify,
                                           lr: 0.01})

    plt.subplot(2,1,1)
    plt.xlim([0,50])
    plt.plot(range(len(y_verify)), y_pred,'b--')
    plt.plot(range(len(y_verify)), y_verify,'r')
    plt.title('validation')

    y_ss = sess.run(y_predict, feed_dict={x: x_train,
                                           y: y_train.reshape(-1, 1),
                                           lr: 0.01})
    plt.subplot(2,1,2)
    plt.xlim([0,50])
    plt.plot(range(len(y_train)), y_ss,'r--')
    plt.plot(range(len(y_train)), y_train,'b')
    plt.title('train')

    plt.savefig('tf.png')
    plt.show()

    r_square(y_verify, y_pred)

训练了大概3000个epoch后，保存模型，之后可以多次训练，但是loss基本收敛了，没有太大变化。

输出结果如下：

final loss =  15.117827
var: 99.0584735569471
MSE-ljj: 15.11782691349897
R2-ljj： 0.8473848185757882

从图像上看，拟合效果也是一般，再拿一个放大版本的validation图，同样取前50个样本，这样方便和之前的线性回归模型对比。

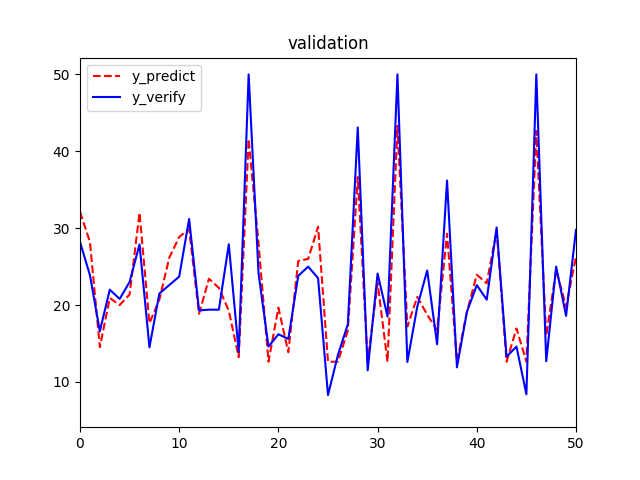
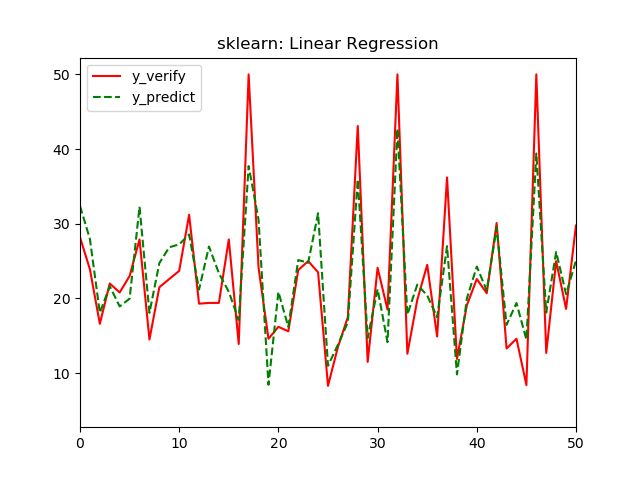
最后我们还是用数据来说明：

tf模型结果中，

R2：0.847   > 0. 779

MSE：15.1  < 21.8

都比sklearn的线性回归结果要好。所以，此tf模型对波士顿房价数据的可解释性更强。