平衡树与AVL
1、二分搜索树存在的问题

如果数据是顺序添加到二分搜索树,二分搜索树会退化成一个链表,这就好大大降低二分搜索树的效率。
如何解决这个问题呢?
需要添加一种机制,使得二分搜索树维持平衡二叉树的性质。AVL树就是一种经典的平衡二叉树。
2、AVL树介绍
AVL的名称来自俄罗斯两位科学的名字 G.M.Adelson-Velsky和E.M.Landis
1962年的论文首次提出
最早的自平衡二分搜索树结构。
3、平衡二叉树
什么是平衡二叉树?
1)、对于任意一个节点,左子树和右子树的高度差不能超过1
如下图所示的平衡二叉树

12的左子树高度为3,右子树高度为2,相差不超过1
8的左子树高度为2,右子树高度为1,相差不超过1
18的左子树高度为1,右子树高度为0,相差不超过1
2) 平衡二叉树的高度和节点数量的关系也是O(logn)的
3) 标准节点的高度
4) 计算平衡因子
下图,黑色数字为高度,蓝色数字为平衡因子(左右两棵树的高度差)。因为节点12和节点8的左右子树高度差超过了1,所有不是平衡二叉树。

一个满二叉树一定是平衡二叉树
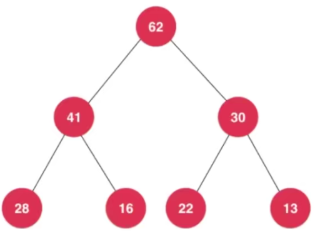
完全二叉树是平衡二叉树
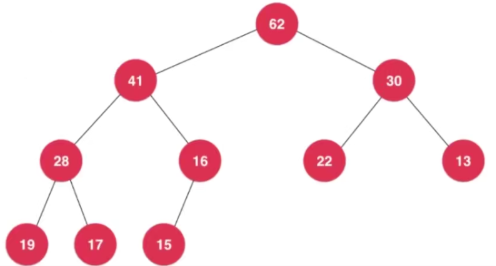
线段树是平衡二叉树
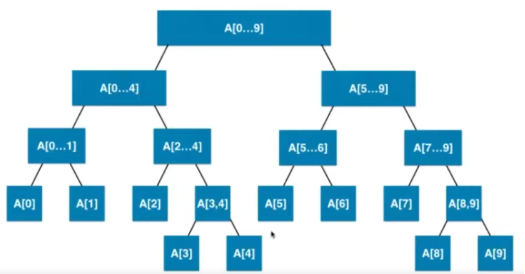
4、平衡二叉树实现
1) 平衡二叉树基本定义
基于二分搜索树实现,并且Node有key,value和节点的高度。
public class AVLTree<K extends Comparable<K>, V> {
private class Node{
public K key;
public V value;
//节点的高度
public int height;
//左孩子
public Node left;
//右孩子
public Node right;
public Node(K key, V value){
this.key = key;
this.value = value;
left = null;
right = null;
//默认节点高度为1
height = 1;
}
}
private Node root;
private int size;
public AVLTree(){
root = null;
size = 0;
}
//判断该二分搜索树是否是一棵二分搜索树
public boolean isBinarySearchTree(){
ArrayList<K> keys = new ArrayList<K>();
inOrder(root, keys);
for(int i = 1; i < keys.size(); i++){
// 不是升序
if(keys.get(i - 1).compareTo(keys.get(i)) > 0){
return false;
}
}
return true;
}
//判断该二叉树是否是一棵平衡二叉树
public boolean isBalanced(){
return isBalanced(root);
}
public boolean isBalanced(Node node){
if(node == null){
return true;
}
int balanceFactory = getBalanceFactory(node);
if(Math.abs(balanceFactory) > 1){
return false;
}
return isBalanced(node.left) && isBalanced(node.right);
}
//中序遍历
private void inOrder(Node node, ArrayList<K> keys) {
if(node == null){
return;
}
inOrder(node.left, keys);
keys.add(node.key);
inOrder(node.right,keys);
}
// 获得节点node的高度
private int getHeight(Node node){
if(node == null){
return 0;
}
return node.height;
}
//获得节点node的平衡因子
private int getBalanceFactory(Node node){
if(node == null){
return 0;
}
return getHeight(node.left) - getHeight(node.right);
}
//向二分搜索树中添加新的元素key,value
public void add(K key, V value){
root = add(root, key, value);
}
//向以node为根的二分搜索树种插入元素key,value,递归算法
public Node add(Node node, K key, V value){
if(node == null){
size ++;
return new Node(key, value);
}
if(key.compareTo(node.key) < 0){
node.left = add(node.left, key, value);
}else if(key.compareTo(node.key) > 0){
node.right = add(node.right, key, value);
}else { //key.compareTo(node.key) = 0
node.value = value;
}
//更新当前节点的高度。 左右孩子节点最大的高度 + 1
node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));
//计算平衡因子
int balanceFactory = getBalanceFactory(node);
//平衡因子大于1,则不满足平衡二叉树
if(Math.abs(balanceFactory) >1 ){
System.out.println("平衡因子=" + balanceFactory);
}
return node;
}
public boolean contains(K key) {
return getNode(key) != null;
}
public V get(K key) {
Node node = getNode(key);
return node != null ? node.value : null;
}
public void set(K key, V newValue) {
Node node = getNode(key);
if(node == null){
throw new IllegalArgumentException(key + " doesn't exist");
}
node.value = newValue;
}
private Node getNode(K key){
return getNode(root, key);
}
private Node getNode(Node node, K key){
if(node == null){
return null;
}
if(key.compareTo(node.key) == 0){
return node;
} else if(key.compareTo(node.key) < 0){
return getNode(node.left, key);
}else { //if(key.compareTo(node.key) > 0)
return getNode(node.right, key);
}
}
public int getSize() {
return size;
}
public boolean isEmpty() {
return size == 0;
}
}
5、平衡二叉树(AVL树)左旋转和右旋转
平衡二叉树是如何实现自平衡的 :左旋转和右旋转
什么时候维护平衡
当插入一个节点时,平衡可能被打破,这时候需要维护平衡
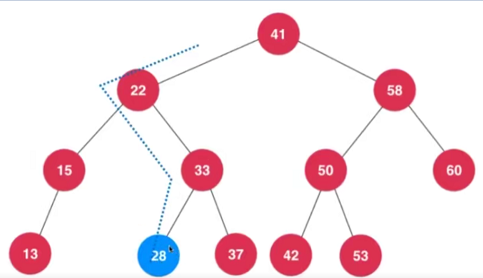
平衡性的破坏反应在这个节点的父亲节点和祖先节点上。因为插入的节点后,这个节点的父亲节点和祖先节点的高度发生了更新。更新后,平衡因子发生了变化。
加入节点后,沿着节点向上维护平衡性。

如上图所示,左边的树当插入5,节点12的平衡因子为2,打破了平衡。
右边树当插入0后,节点8的平衡因子为2,打破了平衡。
右旋转(RR)
如下图所示: T1 < z < T2 < x < T3 < y < T4
y节点的平衡因子为2,违法了平衡性
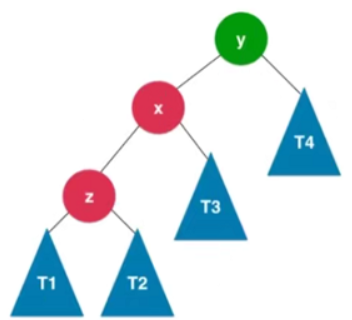
然后进行x.right = y操作

最后进行y.left = T3操作。这样就变成如下图所示的树。这个过程称为右旋转。

此时这棵树即满足二分搜索树的性质,又满足平衡二叉树的性质。
有旋转变化前后分析

假设T1,T2 的最大高度为h,则z为h+1, T3为h+1或者h; x为h+2; T4为h;
修改后,z为h+1不变; T3为h+1或者h; T4为h;y为h+2或者h+1,所以x为h+2或者h+3.
// 对节点y进行右旋转操作,返回旋转后新的根节点x
// y x
// / /
// x T4 向右旋转(y) z y
// / -----------> / /
// z T3 T1 T2 T3 T4
// /
// T1 T2
private Node rightRotate(Node y){
Node x = y.left;
Node T3 = x.right;
//向右旋转过程
x.right = y;
y.left = T3;
//更新height
y.height = 1 + Math.max(getHeight(y.left), getHeight(y.right));
x.height = 1 + Math.max(getHeight(x.left), getHeight(x.right));
return x;
}
add方法增加rightRotate
//向以node为根的二分搜索树种插入元素key,value,递归算法
public Node add(Node node, K key, V value){
if(node == null){
size ++;
return new Node(key, value);
}
if(key.compareTo(node.key) < 0){
node.left = add(node.left, key, value);
}else if(key.compareTo(node.key) > 0){
node.right = add(node.right, key, value);
}else { //key.compareTo(node.key) = 0
node.value = value;
}
//更新当前节点的高度。 左右孩子节点最大的高度 + 1
node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));
//计算平衡因子
int balanceFactory = getBalanceFactory(node);
//平衡因子大于1,则不满足平衡二叉树
if(Math.abs(balanceFactory) >1 ){
System.out.println("平衡因子=" + balanceFactory);
}
//平衡维护
if(balanceFactory > 1 && getBalanceFactory(node.left) >= 0){
return rightRotate(node);
}
return node;
}
左旋转(LL)
插入的元素在不平衡的节点的右侧的右侧
T4< y < T3 < x <T1 < z < T2
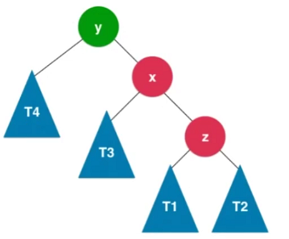
首先执行x.left = y操作

然后执行x.right=T3

此时这棵树即满足二分搜索树的性质,又满足平衡二叉树的性质。
代码实现:
// 对节点y进行右旋转操作,返回旋转后新的根节点x
// y x
// / /
// T1 x 向左旋转(y) y z
// / -----------> / /
// T2 z T1 T2 T3 T4
// /
// T1 T2
private Node leftRotate(Node y){
Node x = y.right;
Node T2 = x.left;
//向右旋转过程
x.left = y;
y.right = T2;
//更新height
y.height = 1 + Math.max(getHeight(y.left), getHeight(y.right));
x.height = 1 + Math.max(getHeight(x.left), getHeight(x.right));
return x;
}
add方法增加leftRotate
//向以node为根的二分搜索树种插入元素key,value,递归算法
public Node add(Node node, K key, V value){
if(node == null){
size ++;
return new Node(key, value);
}
if(key.compareTo(node.key) < 0){
node.left = add(node.left, key, value);
}else if(key.compareTo(node.key) > 0){
node.right = add(node.right, key, value);
}else { //key.compareTo(node.key) = 0
node.value = value;
}
//更新当前节点的高度。 左右孩子节点最大的高度 + 1
node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));
//计算平衡因子
int balanceFactory = getBalanceFactory(node);
//平衡因子大于1,则不满足平衡二叉树
if(Math.abs(balanceFactory) >1 ){
System.out.println("平衡因子=" + balanceFactory);
}
//平衡维护 getBalanceFactory(node.left) >= 0树向左倾斜
if(balanceFactory > 1 && getBalanceFactory(node.left) >= 0){
return rightRotate(node);
}
// getBalanceFactory(node.right) >= 0树向右倾斜
if(balanceFactory > -1 && getBalanceFactory(node.right) >= 0){
return leftRotate(node);
}
return node;
}
插入的元素在不平衡的节点的左侧的右侧(LR)

首先对x进行左旋转。
如下图所示,转化为LL(左旋转)的情况,对y节点进行右旋转

RL

先对x节点进行右旋转,如下图所示,转化为RR(右旋转)的情况

完整的代码如下:
public class AVLTree<K extends Comparable<K>, V> {
private class Node{
public K key;
public V value;
//节点的高度
public int height;
//左孩子
public Node left;
//右孩子
public Node right;
public Node(K key, V value){
this.key = key;
this.value = value;
left = null;
right = null;
//默认节点高度为1
height = 1;
}
}
private Node root;
private int size;
public AVLTree(){
root = null;
size = 0;
}
//判断该二分搜索树是否是一棵二分搜索树
public boolean isBinarySearchTree(){
ArrayList<K> keys = new ArrayList<K>();
inOrder(root, keys);
for(int i = 1; i < keys.size(); i++){
// 不是升序
if(keys.get(i - 1).compareTo(keys.get(i)) > 0){
return false;
}
}
return true;
}
//判断该二叉树是否是一棵平衡二叉树
public boolean isBalanced(){
return isBalanced(root);
}
public boolean isBalanced(Node node){
if(node == null){
return true;
}
int balanceFactory = getBalanceFactor(node);
if(Math.abs(balanceFactory) > 1){
return false;
}
return isBalanced(node.left) && isBalanced(node.right);
}
//中序遍历
private void inOrder(Node node, ArrayList<K> keys) {
if(node == null){
return;
}
inOrder(node.left, keys);
keys.add(node.key);
inOrder(node.right,keys);
}
// 获得节点node的高度
private int getHeight(Node node){
if(node == null){
return 0;
}
return node.height;
}
// 获得节点node的平衡因子
private int getBalanceFactor(Node node){
if(node == null) {
return 0;
}
return getHeight(node.left) - getHeight(node.right);
}
// 向二分搜索树中添加新的元素(key, value)
public void add(K key, V value){
root = add(root, key, value);
}
// 向以node为根的二分搜索树中插入元素(key, value),递归算法
// 返回插入新节点后二分搜索树的根
private Node add(Node node, K key, V value){
if(node == null){
size ++;
return new Node(key, value);
}
if(key.compareTo(node.key) < 0) {
node.left = add(node.left, key, value);
}
else if(key.compareTo(node.key) > 0) {
node.right = add(node.right, key, value);
}
else {// key.compareTo(node.key) == 0
node.value = value;
}
// 更新height
node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));
// 计算平衡因子
int balanceFactor = getBalanceFactor(node);
// 平衡维护
if (balanceFactor > 1 && getBalanceFactor(node.left) >= 0) {
return rightRotate(node);
}
if (balanceFactor < -1 && getBalanceFactor(node.right) <= 0) {
return leftRotate(node);
}
if (balanceFactor > 1 && getBalanceFactor(node.left) < 0) {
node.left = leftRotate(node.left);
return rightRotate(node);
}
if (balanceFactor < -1 && getBalanceFactor(node.right) > 0) {
node.right = rightRotate(node.right);
return leftRotate(node);
}
return node;
}
// 对节点y进行右旋转操作,返回旋转后新的根节点x
// y x
// / /
// x T4 向右旋转(y) z y
// / -----------> / /
// z T3 T1 T2 T3 T4
// /
// T1 T2
private Node rightRotate(Node y) {
Node x = y.left;
Node T3 = x.right;
// 向右旋转过程
x.right = y;
y.left = T3;
// 更新height
y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;
x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;
return x;
}
// 对节点y进行右旋转操作,返回旋转后新的根节点x
// y x
// / /
// T1 x 向左旋转(y) y z
// / -----------> / /
// T2 z T1 T2 T3 T4
// /
// T1 T2
private Node leftRotate(Node y) {
Node x = y.right;
Node T2 = x.left;
// 向左旋转过程
x.left = y;
y.right = T2;
// 更新height
y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;
x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;
return x;
}
public boolean contains(K key) {
return getNode(key) != null;
}
public V get(K key) {
Node node = getNode(key);
return node != null ? node.value : null;
}
public void set(K key, V newValue) {
Node node = getNode(key);
if(node == null){
throw new IllegalArgumentException(key + " doesn't exist");
}
node.value = newValue;
}
private Node getNode(K key){
return getNode(root, key);
}
private Node getNode(Node node, K key){
if(node == null){
return null;
}
if(key.compareTo(node.key) == 0){
return node;
} else if(key.compareTo(node.key) < 0){
return getNode(node.left, key);
}else { //if(key.compareTo(node.key) > 0)
return getNode(node.right, key);
}
}
public int getSize() {
return size;
}
public boolean isEmpty() {
return size == 0;
}
public static void main(String[] args) {
//数据准备
ArrayList<String> list = new ArrayList<String>();
String[] arr = {"张三", "李四","王五", "赵六","张三丰","李思明","王老五","赵明"};
for(int i = 0; i < 10; i++){
for(String str : arr){
String key = str +i;
list.add(key);
}
}
for(int i = 0; i < 5000; i++){
for(String str : arr){
String key = str +i;
list.add(key);
}
}
System.out.println("准备的数据数量=" + list.size());
AVLTree<String, Integer> map = new AVLTree();
for(String key: list){
Integer value = map.get(key);
if(value == null){
map.add(key, 1);
}else {
map.add(key, value +1);
}
}
System.out.println("Map size: " + map.getSize());
String key = "张三0";
System.out.println(key + "出现的次数:" + map.get(key));
boolean isBinarySearchTree = map.isBinarySearchTree();
System.out.println("是否是二分搜索树" + isBinarySearchTree);
boolean isBalanced = map.isBalanced();
System.out.println("是否是平衡二叉树" + isBalanced);
}
}
6、平衡二叉树与二分搜索树对比
public static void main(String[] args) {
//数据准备
ArrayList<String> list = new ArrayList<String>();
String[] arr = {"张三", "李四","王五", "赵六","张三丰","李思明","王老五","赵明"};
for(int i = 0; i < 100000; i++){
for(String str : arr){
String key = str +i;
list.add(key);
}
}
System.out.println("准备的数据数量=" + list.size());
long startTime = System.nanoTime();
AVLTree<String, Integer> avlTree = new AVLTree();
for(String key: list){
Integer value = avlTree.get(key);
if(value == null){
avlTree.add(key, 1);
}else {
avlTree.add(key, value +1);
}
}
for(String key: list){
avlTree.contains(key);
}
long endTme = System.nanoTime();
double spend = (endTme - startTime) / 1000000000.0;
System.out.println("平衡二叉树耗时"+ spend +"秒");
startTime = System.nanoTime();
BinarySearchTreeMap<String, Integer> bst = new BinarySearchTreeMap();
for(String key: list){
Integer value = bst.get(key);
if(value == null){
bst.add(key, 1);
}else {
bst.add(key, value +1);
}
}
for(String key: list) {
bst.contains(key);
}
endTme = System.nanoTime();
spend = (endTme - startTime) / 1000000000.0;
System.out.println("二分搜索树耗时"+ spend +"秒");
}
输出结果:
准备的数据数量=800000
平衡二叉树耗时0.828722897秒
二分搜索树耗时1.229801731秒
可以看到平衡二叉树耗时更短。
7、平衡二叉树的删除
// 返回以node为根的二分搜索树的最小值所在的节点
private Node minimum(Node node){
if(node.left == null)
return node;
return minimum(node.left);
}
// 删除掉以node为根的二分搜索树中的最小节点
// 返回删除节点后新的二分搜索树的根
private Node removeMin(Node node){
if(node.left == null){
Node rightNode = node.right;
node.right = null;
size --;
return rightNode;
}
node.left = removeMin(node.left);
return node;
}
// 从二分搜索树中删除键为key的节点
public V remove(K key){
Node node = getNode(root, key);
if(node != null){
root = remove(root, key);
return node.value;
}
return null;
}
private Node remove(Node node, K key){
if( node == null )
return null;
if( key.compareTo(node.key) < 0 ){
node.left = remove(node.left , key);
return node;
}
else if(key.compareTo(node.key) > 0 ){
node.right = remove(node.right, key);
return node;
}
else{ // key.compareTo(node.key) == 0
// 待删除节点左子树为空的情况
if(node.left == null){
Node rightNode = node.right;
node.right = null;
size --;
return rightNode;
}
// 待删除节点右子树为空的情况
if(node.right == null){
Node leftNode = node.left;
node.left = null;
size --;
return leftNode;
}
// 待删除节点左右子树均不为空的情况
// 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
// 用这个节点顶替待删除节点的位置
Node successor = minimum(node.right);
successor.right = removeMin(node.right);
successor.left = node.left;
node.left = node.right = null;
return successor;
}
}