个人备查笔记,
仅作为实现方法的记录...
给出的公式并不全是最佳求解公式,
核心概念:
1.几何投影和齐次坐标-Model-View-Projection概念:
https://developer.mozilla.org/zh-CN/docs/Web/API/WebGL_API/WebGL_model_view_projection
2.反射矩阵(reflection matrix):
https://en.wikipedia.org/wiki/Transformation_matrix#Reflection_2
记:
矩阵4x4:(4x4针对齐次坐标,这里使用单位向量,所以仅表示反射方向)
glsl:
vec4 cur_pos = [1,1,0,1]; vec3 n = vec3(0,0,1); n = normalize(n); float a = n.x; float b = n.y; float c = n.z; mat4 reflectMat = mat4( 1.0 - 2.0 * a * a , -2.0 * b * a , -2.0 * c * a , 0.0 , -2.0 * a * b , 1.0 - 2.0 * b * b , -2.0 * c * b , 0.0 , -2.0 * a * c , -2.0 * b * c , 1.0 - 2.0 * c * c , 0.0 , 0.0 , 0.0 , 0.0 , 1.0 ); vec4 new_pos = relfectMat * cur_pos;
这里列出一些自己常用到的数学或物理等应用场景的基础公式和基于UE4实现的的例子(BP或C++),备查
(随缘更新)
数学:
关于循环数列:
循环数列的通项公式在计算机的运用
计算机中 常用cos(n*x) 与sin( pi/2 -n*pi)来代替 (-1)^n做周期循环....
3d中常用来做一个周期时间内的顶点变换循环(如海浪动态材质就是用循环数列实现)
概念: https://wenku.baidu.com/view/0d0c214df7ec4afe04a1dfcf.html
求(直线L)到平面的交点:
公式:
wait
UE4求点到平面的交点的交点实现:
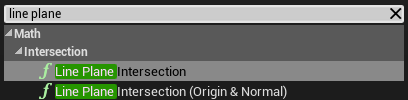
仿射变换和射影变换:
Q.Actor A到Actor B的方向v:
相当于线段AB的单位向量v
1.线性插值:
v = (B - A) / (∥ B - A∥)
UE4实现(BP):
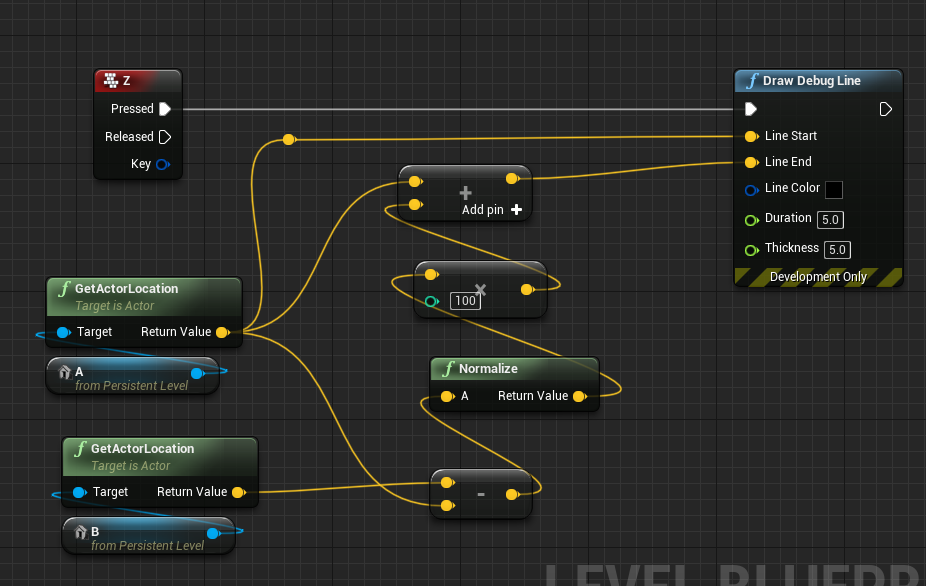
问.点P到直线L1的距离D:
直线L1上任意一点P1,单位向量为V1
距离D = (P - P1) · (P - P1) - ( ( (P - P1) · V1)^2 / V1 · V1 )
问.两直线或平面的交点P3或交线L3
Note:克莱姆法则:https://en.wikipedia.org/wiki/Cramer%27s_rule
交点:
L1:单位向量V1,L1上任意一点P1 有方程式:P3 = P1 + kV1
L2:单位向量V2,L2上任意一点P2 有方程式:P3 = P2 + tV2
首先假设,线段 L1和L2相交,即V1叉乘 V2不等于 0
可推到线性方程组未知数(k,t): (V1 · V1 )k - (V1 · V2 )t = V1(P2 - P1)
(V1 · V2 )k - (V2 · V2 )t = V2(P2 - P1)
利用克莱姆法则可得k与t的解.
带入L1或L2可得P3
交线:
Note:V1和V2必须为单位向量
公式:L3 = ( ( V1 · P1 ) (V1 - (V1 · V2)V2 ) + ( V2 · P2 )( V2 - (V1 · V2)V1 ) ) ÷ (1 - (V1 · V2)^2 )
UE4例子:
交点:
wait
交线 :



问.Actor A绕任意轴Axes(u,O)旋转θ度:求Actor A的新位置 P:
u是Normal Vector(单位向量)
O是旋转轴上任意一点 Vector.
通常常用几种方式实现:
1.带入旋转公式(点乘(·)和叉乘(×)):
那么P = O + ( Cosθ )( A - O ) + (1 - cosθ)(( A - O ) · u)u + ( sinθ )u × ( A - O )
2.四元数(Slerp):
wait
3.矩阵:
3D旋转矩阵mat3x3:
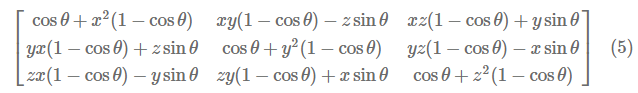
3D旋转矩阵mat4x4():
找不到图,其实就是在mat3x3 旋转矩阵上补位:
glsl:
float s = sin(theta); float c = cos(theta); float oc = 1.0 - c; mat4 rotate_mat = mat4( oc * n.x * n.x + c, oc * n.x * n.y + n.z * s, oc * n.z * n.x - n.y * s, 0.0, oc * n.x * n.y - n.z * s, oc * n.y * n.y + c, oc * n.y * n.z + n.x * s, 0.0, oc * n.z * n.x + n.y * s, oc * n.y * n.z - n.x * s, oc * n.z * n.z + c, 0.0, 0.0, 0.0, 0.0, 1.0 );
4.Rodrigues旋转公式(罗德里格斯旋转公式):
基本公式(glsl代码):
p是需要旋转的点
n 是旋转轴的方向(单位向量)
theta是饶n轴旋转的弧度
vec3 rotatePoint(vec3 p, vec3 n, float theta) {
return (
p * cos(theta) + cross(n, p) *
sin(theta) + n * dot(p, n) *
(1.0 - cos(theta))
);
}
note:这里假定为原点.如果轴不再原点可先平移变换,在平移回去
如果绕线段旋转需要先用点乘求出点到线段的垂直点,实现方法,请参考UE4的ClosestPointOnSegment和ClosestPointOnLine函数
UE4实现:
Ue4已经实现,3D旋转矩阵:请参考UKismetMathLibrary::RotateAngleAxis或FVector::RotateAngleAxis
几何:
wait
图形:
Q.求多边形的包容矩形(AABB):
公式:(图片来自网络不知出处-_-! )

UE4例子:
wait
Q.点P是否在平面S上:
方式一,用度量公式:
假设平面S法线N和平面上任意一点O
当 (P-O) · N = 0 则 点P在平面S上
栗子:
wait
材质公式相关:
Q.图形学-Frenel函数材质球实现方式:
|
调个材质 大概公式 自发光= 自定义边光颜色* ((1-法线与视角方向点乘)的 自定义幂次方 ) 这个是比较简单方法
|
|
模型的法线与视角方向 角度越大 表示是约边缘地方 反之不是 角度越大点成越小 1 - 点成 越大 然后 再次 幂次方 更大 所以颜色看起来 边缘就有金边了
|
栗子: