
题意是给定一个N × N大小的棋盘,求不同的N皇后方案的个数。N皇后的方案指,N个皇后放在棋盘上,互相不能攻击到。
国际象棋里,皇后可以横竖斜走若干步,所以一个方案是合法的,必须满足任意一个皇后所在的行、列、对角线、斜对角线都没有其他皇后。
我们要求的就是这样的方案的个数。
由于每行只能放一个皇后,所以我们可以按照行来搜索方案(当然按列或者对角线/斜对角线也可,不过按行来搜索代码比较好写),
要满足互相不攻击的条件,我们在搜索每一行的时候,都需要枚举这一行可以放皇后的位置,可以放皇后的条件就是:
当前位置的列、对角线、斜对角线上都没有其他皇后,只要满足这个条件,就可以在当前位置放一个皇后,然后继续搜索下一行。
所以显然这就是一个DFS + 回溯,DFS结束的条件就是搜索到了最后一行(的下一个位置),也就是找到一个每一行都可以放下一个皇后且不冲突的方案。
这时就在结果数组里记录下方案数。当DFS(0)执行结束(表示从第0行开始递归搜索所有解方案)时,我们就找到了所有的方案。
这里的关键就是如何判断当前要判断的位置是否冲突,如何判断这个位置所在的列、对角线、斜对角线上是否有其他皇后呢?
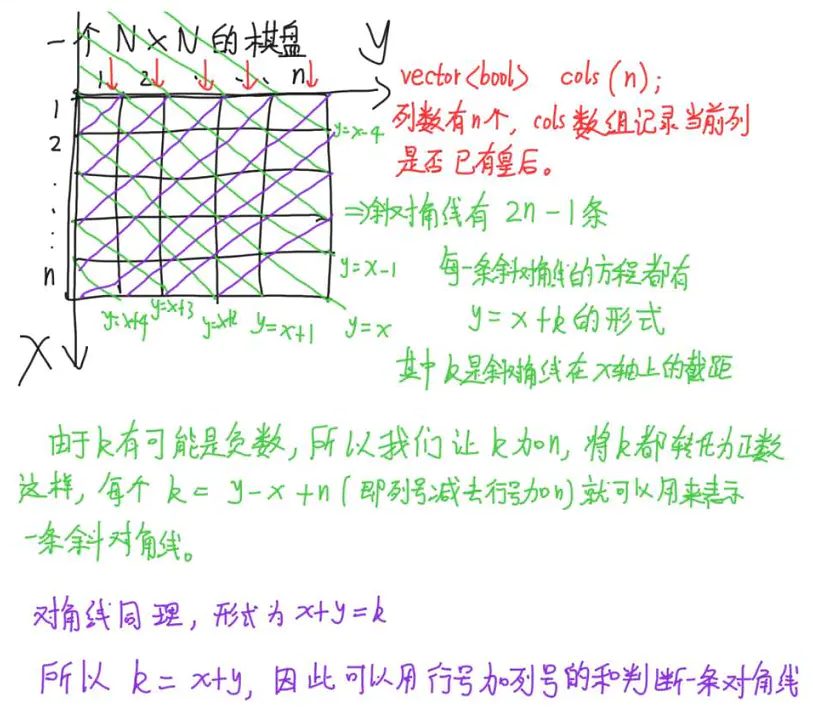
如上图所示,红色线为列,绿色线为斜对角线,紫色线为对角线。
对于列,其实很好判断,只要开一个大小为n的bool数组,记录每一列上是否已有皇后即可。
对于斜对角线(这里认为对角线是棋盘从左上到右下的斜线)的判断,我们可以寻找规律,我们把棋盘从上向下作为横坐标x,从左到右作为纵坐标y。
首先可以发现一共有2 * n - 1条对角线,对于每一条斜对角线,都有一个y = x + k的形式,比如最中间的斜对角线(即棋盘左上角到右下角的斜对角线
就满足方程y=x),移项得到k = y - x(即k等于列号减去行号),所以k是斜对角线在x轴的截距,
所以我们可以根据截距k来判断当前位置属于哪一条斜对角线,从k = y - x这个公式可以看出,
k有可能为负数(截距k在x轴负半轴),我们可以给所有截距都加上一个n,将截距k变为正数。
对于对角线(这里认为斜对角线是棋盘从右上到左下的斜线)的判断,可以发现规律,对角线都满足方程x + y = k(这里的k不是斜对角线的k了),
所以我们可以直接根据x + y的值(即行和列的和)来判断当前位置属于哪个对角线。
所以按行搜索的时候,对于每一行的所有位置我们都枚举一遍,看看每个位置上所在的列、对角线、斜对角线上是否都没有其他皇后了,
如果没有,说明当前位置可以放皇后,就先放一个皇后,然后递归再搜索下一行,直到搜索到最后一行(的下一个位置)或者枚举完所有的位置,
表示找到可行的方案或者找不到。
代码如下:
class Solution {
vector<vector<string>> res; //结果数组,保存所有可行方案的棋盘
vector<string> oneSolution; //记录一个可行方案
int n; //n是棋盘大小,这里要记录到一个全局变量里,方便对于下面三个数组以及上面的oneSolution数组大小的初始化
vector<bool> cols, diagram, anti_diagram; //分别判断列、对角线、斜对角线上是否有皇后
public:
vector<vector<string>> solveNQueens(int _n) {
n = _n;
cols = vector<bool>(n); //把n记录到全局变量里,就是为了这里给四个数组赋予一定大小
diagram = anti_diagram = vector<bool>(2 * n); //对角线和斜对角线分别由2 * n - 1条
oneSolution = vector<string>(n, string(n, '.')); //最开始令棋盘全部为'.'
DFS(0); //从第0行开始搜索
return res;
}
void DFS(int curRow) { //传入参数curRow表示当前正在搜索的行
if(curRow == n) { //如果搜索到最后一行的下一个位置,表示找到了一个可行解
res.push_back(oneSolution); //记录当前棋盘
return ;
}
for(int i = 0; i < n; ++i) { //搜索当前行的所有列,判断是否可以放置皇后(即不产生冲突)
if(cols[i] == false && diagram[curRow - i + n] == false && anti_diagram[curRow + i] == false) { //如果当前位置所在列、对角线、斜对角线上都没有皇后,则可以在当前位置放一个皇后
cols[i] = diagram[curRow - i + n] = anti_diagram[curRow + i] = true; //搜索下一行之前,需要先记录当前列、对角线、斜对角线上已经有皇后
oneSolution[curRow][i] = 'Q'; //“放皇后”,在棋盘上将'.'修改为'Q'
DFS(curRow + 1); //继续搜索下一行
oneSolution[curRow][i] = '.'; //DFS回溯要恢复现场,且一定和DFS之前的操作是对称的,之前将当前位置改为'Q',现在要改回去
cols[i] = diagram[curRow - i + n] = anti_diagram[curRow + i] = false; //还要修改当前列、对角线、斜对角线的状态为没有皇后
}
}
}
};