LeetCode240. 搜索二维矩阵 II

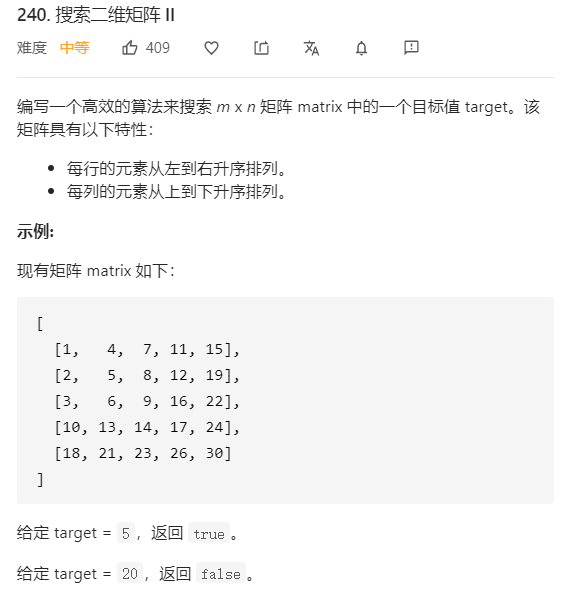
给定二维矩阵，搜索是否存在目标值target，暴力做法可以两重循环遍历数组进行搜索，这样时间复杂度是O(rows * cols)，
其中rows，cols为二维矩阵matrix的行数和列数。

我们可以用给定的性质进行优化，因为每行的元素从左到右升序排列，每列的元素从上到下升序排列。
所以我们可以从右上角的元素开始搜索（因为右上角的元素是这一行最大的，这一列最小的），每次把右上角的元素与target进行比较，
如果相等，很好，我们找到了target，返回true；

如果右上角的元素大于target,由于最后一列的所有元素都大于等于右上角的元素，所以最后一列的所有元素都不可能是target，
所以我们“删除”最后一列，从剩下的矩阵里再用（新的）右上角元素和target进行比较；

如果右上角的元素小于target，由于第一行的所有元素都小于等于右上角的元素，所以第一行的所有元素都不可能是target，
所以我们“删除”第一行，从剩下的矩阵里再用（新的）右上角元素和target进行比较。

如果删除完所有的行和列还是没找到target，则矩阵中不存在target，返回false。

时间复杂度分析：每一次比较，要么找到了target，要么就删除了一行或者一列，所以时间复杂度是O(rows + cols），rows和cols是
matrix矩阵的行数和列数。

代码如下：

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        if(matrix.size() == 0 || matrix[0].size() == 0) {                  //矩阵为空，返回false
            return false;
        }
        int rows = matrix.size(), cols = matrix[0].size();
        int x = 0, y = cols - 1;                                           //matrix[x][y]是右上角元素
        while(x < rows && y >= 0) {                                        //每删除一行x就加一，每删除一列y就加一，所以越界的情况就是x==rows或者y<0
            if(matrix[x][y] == target) {                              
                return true;
            } else if(matrix[x][y] > target) {                             //删除一列等价于：用matrix[x][y - 1]代表新的右上角元素
                --y;
            } else if(matrix[x][y] < target) {                             //删除一行等价于：用matrix[x + 1][y]代表新的右上角元素
                ++x;
            }
        }
        return false;                                          //删除所有的行或列后也没有找到target，返回false
    }
};