[数据结构

一、什么是顺序表？

使用顺序存储方式的顺序表即为顺序表，存取时间性能为 O(1)，示意图如下所示：

二、顺序表的基本操作（用静态数组实现）

在编写顺序表的基本操作函数前，有几个注意点：

• 插入操作中，需考虑顺序表已满的情况，删除、获取操作中，需考虑顺序表为空的情况；
• 在各操作中，当涉及到位置 i 时，都应考虑 i 位置不合理的情况；
• 插入删除操作中，均应考虑插入或删除位置为表尾（或表尾下一个位置）的情况；

2.1 顺序表的结构定义

既然顺序表的每个数据元素的类型都相同，所以可以用 C 语言的一维数组来实现顺序存储结构，即把第一个数据元素存到数组下标为 0 的位置中，接着把顺序表相邻的元素存储在数组中相邻的位置。

来看（静态顺序）顺序表的顺序存储的结构定义。

#define MAX_SIZE 100  /* 数组长度 */
typedef int  ElemType; /* "ElemType类型根据实际情况而定， 这里假设为int */
// 顺序表结构定义
typedef struct
{
	ElemType  data[MAX_SIZE];  /* 存放顺序表元素的数组，最大值为MAXSIZE */
	int length; /* 顺序表的当前长度 */
}SeqList;

这里，我们发现顺序存储结构需要三个属性：

• 存储空间的起始位置：数组 data，它的存储位置就是存储空间的存储位置。
• 顺序表的最大存储容量：数组长度 MaxSize。
• 顺序表的当前长度：length。

注意：这里有两个概念 "数组的长度" 和 "顺序表的长度" 需要区分一下。数组的长度是存放顺序表的存储空间的长度，存储分配后这个量是一般是不变的。顺序表的长度是顺序表中数据元素的个数，随着顺序表插入和删除操作的进行，这个量是变化的。

2.2 初始化操作

实现代码如下：

// 初始化操作
SeqList *initList()
{
	SeqList *pSeqList = (SeqList *)malloc(sizeof(SeqList));
	if (pSeqList == NULL)
	{
		printf("initList malloc error!
");
		exit(-1);
	}

	pSeqList->length = 0;
	return pSeqList;
}

2.3 插入操作

插入数据的实现过程如下图所示：

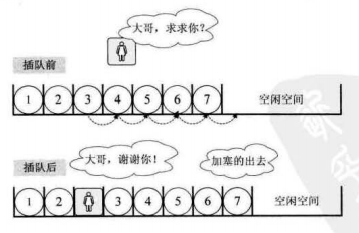
插入算法的思路;

• 判断顺序表是否已满，且插入位置是否合理;
• 从最后一个元素开始向前遍历到第 i 个位置，分别将它们都向后移动一个位置;
• 将要插入元素填入位置i处;
• 表长加1。

实现代码如下：

// 插入元素操作
Status insertList(SeqList *pSeqList, int i, const ElemType e)
{
	// 判断顺序表是否已满，且插入位置是否合理
	if (pSeqList->length >= MAX_SIZE || i < 0 || i > pSeqList->length) // 可以在表尾的下一个位置插入元素
		return FALSE;

	// 从最后一个元素开始向前遍历到第i个位置，分别将它们都向后移动一个位置
	// 这种特殊情况不用后移：在表尾的下一个位置插入元素(包含第一次在位置0插入元素的情况)
	if (i != pSeqList->length)
	{
		// 将插入位置及后面元素向后移动一位
		for (int k = pSeqList->length - 1; k >= i; k--)
			pSeqList->data[k + 1] = pSeqList->data[k];
	}

	// 将要插入元素填入位置i处
	pSeqList->data[i] = e;
	// 表长加1
	pSeqList->length++;

	return TRUE;
}

2.4 删除操作

顺序表的顺序存储结构删除元素的过程如下图所示：

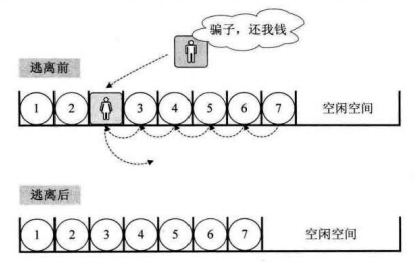
删除算法的思路：

• 判断顺序表是否已满，且插入位置是否合理;
• 取出删除元素;
• 从删除元素的下一个位置开始遍历到最后一个元素位置，分别将它们都向前移动一个位置;
• 表长减1。

实现代码如下：

// 删除元素操作
Status deleteList(SeqList *pSeqList, int i, ElemType *e)
{
	// 判断顺序表是否为空，且删除位置是否合理
	if (pSeqList->length == 0 || i < 0 || i > pSeqList->length - 1)
		return FALSE;

	// 取出删除元素
	*e = pSeqList->data[i];

	// 从删除元素的下一个位置开始遍历到最后一个元素位置，分别将它们都向前移动一个位置
    // 这种特殊情况不用前移：删除位置在表尾
	if (i != pSeqList->length - 1)
	{
		// 将删除元素的下一个位置及后面元素向前移动一位
		for (int k = i; k < pSeqList->length - 1; k++)
			pSeqList->data[k] = pSeqList->data[k + 1];
	}

	// 表长减1
	pSeqList->length--;

	return TRUE;
}

2.5 获取元素操作

对于顺序表的顺序存储结构来说，如果我们要实现 getElem 操作，即将顺序表中的第 i 个位置元素值返回，其实是非常简单的。 只要 i 的数值在数组下标范围内，就是把数组第 i 下标的值返回即可。 来看代码:

// 获取元素操作
Status getElem(SeqList *pSeqList, int i, ElemType *e)
{
	// 判断顺序表是否存在，且删除位置是否合理
	if (pSeqList == NULL || i < 0 || i > pSeqList->length - 1)
		return FALSE;

	*e = pSeqList->data[i];

	return TRUE;
}

三、完整程序

#include <stdio.h>
#include <stdlib.h>

#define TRUE 1
#define FALSE 0
typedef int Status; // Status是函数结果状态，成功返回TRUE,失败返回FALSE

#define MAX_SIZE 100  /* 数组长度 */
typedef int  ElemType; /* "ElemType类型根据实际情况而定， 这里假设为int */
// 顺序表结构定义
typedef struct
{
	ElemType  data[MAX_SIZE];  /* 存放顺序表元素的数组，最大值为MAXSIZE */
	int length; /* 顺序表的当前长度 */
}SeqList;

SeqList *initList(); // 初始化操作
Status appendList(SeqList *pSeqList, const ElemType e); // 附加元素操作
Status insertList(SeqList *pSeqList, int i, const ElemType e); // 插入元素操作
Status deleteList(SeqList *pSeqList, int i, ElemType *e); // 删除元素操作
Status getElem(SeqList *pSeqList, int i, ElemType *e); // 获取元素操作
int locateElem(SeqList *pSeqList, const ElemType e); // 查找元素位置操作
void traverseList(SeqList *pSeqList); // 遍历顺序表
Status isEmpty(SeqList *pSeqList); // 检测是否为空操作
int getLength(SeqList *pSeqList); // 获取元素个数操作
void clearList(SeqList *pSeqList); // 清空顺序表操作
void destroyList(SeqList *pSeqList); // 销毁顺序表操作

// 初始化操作
SeqList *initList()
{
	SeqList *pSeqList = (SeqList *)malloc(sizeof(SeqList));
	if (pSeqList == NULL)
	{
		printf("initList malloc error!
");
		exit(-1);
	}

	pSeqList->length = 0;
	return pSeqList;
}

// 附加元素操作
Status appendList(SeqList *pSeqList, const ElemType e)
{
	// 判断顺序表长度是否大于等于数组长度，是则抛出异常或动态增加容量
	if (pSeqList->length >= MAX_SIZE)
		return FALSE;

	// 在表尾后面添加元素e
	pSeqList->data[pSeqList->length] = e;

	// 表长加1
	pSeqList->length++;

	return TRUE;
}

// 插入元素操作
Status insertList(SeqList *pSeqList, int i, const ElemType e)
{
	// 判断顺序表是否已满，且插入位置是否合理
	if (pSeqList->length >= MAX_SIZE || i < 0 || i > pSeqList->length) // 可以在表尾的下一个位置插入元素
		return FALSE;

	// 从最后一个元素开始向前遍历到第i个位置，分别将它们都向后移动一个位置
	// 有两种特殊情况不用后移：当第一次在位置0插入元素，或者在表尾的下一个位置插入元素
	if (!(pSeqList->length == 0 || i == pSeqList->length))
	{
		// 将插入位置及后面元素向后移动一位
		for (int k = pSeqList->length - 1; k >= i; k--)
			pSeqList->data[k + 1] = pSeqList->data[k];
	}

	// 将要插入元素填入位置i处
	pSeqList->data[i] = e;
	// 表长加1
	pSeqList->length++;

	return TRUE;
}

// 删除元素操作
Status deleteList(SeqList *pSeqList, int i, ElemType *e)
{
	// 判断顺序表是否为空，且删除位置是否合理
	if (pSeqList->length == 0 || i < 0 || i > pSeqList->length - 1)
		return FALSE;

	// 取出删除元素
	*e = pSeqList->data[i];

	// 从删除元素的下一个位置开始遍历到最后一个元素位置，分别将它们都向前移动一个位置
	if (i != pSeqList->length - 1) // 【若删除位置在表尾，则不需要前移】
	{
		// 将删除元素的下一个位置及后面元素向前移动一位
		for (int k = i; k < pSeqList->length - 1; k++)
			pSeqList->data[k] = pSeqList->data[k + 1];
	}

	// 表长减1
	pSeqList->length--;

	return TRUE;
}

// 获取元素操作
Status getElem(SeqList *pSeqList, int i, ElemType *e)
{
	// 判断顺序表是否存在，且删除位置是否合理
	if (pSeqList == NULL || i < 0 || i > pSeqList->length - 1)
		return FALSE;

	*e = pSeqList->data[i];

	return TRUE;
}

// 查找元素位置操作
int locateElem(SeqList *pSeqList, const ElemType e)
{
	// 遍历并显示顺序表元素
	for (int i = 0; i < pSeqList->length; i++)
	{
		if (pSeqList->data[i] == e)
			return i;
	}

	return -1;
}


// 遍历操作
void traverseList(SeqList *pSeqList)
{
	for (int i = 0; i < pSeqList->length; i++)
		printf("%d ", pSeqList->data[i]);
	printf("
");
}

// 检测是否为空操作
Status isEmpty(SeqList *pSeqList)
{
	return pSeqList->length == 0 ? TRUE : FALSE;
}

// 获取元素个数操作
int getLength(SeqList *pSeqList)
{
	return pSeqList->length;
}

// 清空顺序表操作
void clearList(SeqList *pSeqList)
{
	pSeqList->length = 0;
}

// 销毁顺序表操作
void destroyList(SeqList *pSeqList)
{
	free(pSeqList);
	pSeqList = NULL;
}

int main()
{
	// 初始化顺序表
	SeqList *pSeqList = initList();

	// 检测顺序表是否为空
	if (isEmpty(pSeqList))
		printf("顺序表为空！

");
	else
		printf("顺序表不为空！

");

	// 附加元素0-2到顺序表
	printf("附加元素0-2到顺序表!

");
	for (int i = 0; i<3; i++)
	{
		appendList(pSeqList, i);
	}
	printf("
");

	// 在位置2插入元素到顺序表
	printf("在位置2插入元素9到顺序表!

");
	insertList(pSeqList, 2, 9);

	// 在顺序表中删除元素
	int value1;
	if (deleteList(pSeqList, 3, &value1) == FALSE)
	{
		printf("delete error!

");
		return -1;
	}
	printf("在位置3删除元素，删除的元素为：%d

", value1);

	// 获取元素个数
	printf("当前元素个数为%d个

", getLength(pSeqList));

	// 查找元素位置
	printf("查找到元素0的位置为：%d

", locateElem(pSeqList, 0));

	// 遍历并显示顺序表元素
	printf("遍历顺序表： ");
	traverseList(pSeqList);
	printf("
");

	// 清空顺序表
	clearList(pSeqList);
	printf("清空顺序表!
");

	// 销毁顺序表
	destroyList(pSeqList);
	printf("
");

	return 0;
}

输出结果如下图所示：

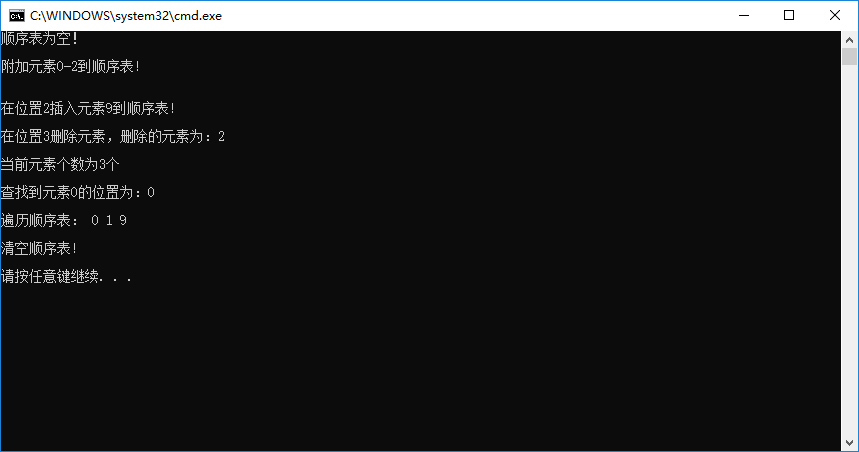
注意上面只是 “静态顺序表” 的 C 语言实现，只实现了一些基本操作，有兴趣的同学可以在这上面扩展；另外测试编译器为 VS2013。

参考：

《大话数据结构 - 第3章》 顺序表