1. 桶排序
1.1 范围为1-M的桶排序
如果有一个数组A,包含N个整数,值从1到M,我们可以得到一种非常快速的排序,桶排序(bucket sort)。留置一个数组S,里面含有M个桶,初始化为0。然后遍历数组A,读入Ai时,S[Ai]增一。所有输入被读进后,扫描数组S得出排好序的表。该算法时间花费O(M+N),空间上不能原地排序。
初始化序列S
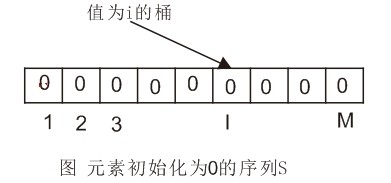
遍历A修改序列S的项
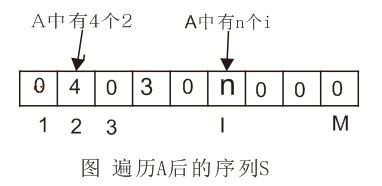
举个例子,排序一个数组[5,3,6,1,2,7,5,10]
值都在1-10之间,建立10个桶:
[0 0 0 0 0 0 0 0 0 0] 桶
[1 2 3 4 5 6 7 8 9 10] 桶代表的值
遍历数组,第一个数字5,第五个桶加1
[0 0 0 0 1 0 0 0 0 0]
第二个数字3,第三个桶加1
[0 0 1 0 1 0 0 0 0 0]
遍历后
[1 1 1 0 2 1 1 0 0 1]
输出
[1 2 3 5 5 6 7 10]
代码
import random
class bucketSort(object):
def _max(self,oldlist):
_max=oldlist[0]
for i in oldlist:
if i>_max:
_max=i
return _max
def _min(self,oldlist):
_min=oldlist[0]
for i in oldlist:
if i<_min:
_min=i
return _min
def sort(self,oldlist):
_max=self._max(oldlist)
_min=self._min(oldlist)
s=[0 for i in xrange(_min,_max+1)]
for i in oldlist:
s[i-_min]+=1
current=_min
n=0
for i in s:
while i>0:
oldlist[n]=current
i-=1
n+=1
current+=1
def __call__(self,oldlist):
self.sort(oldlist)
return oldlist
if __name__=='__main__':
a=[random.randint(0,100) for i in xrange(10)]
bucketSort()(a)
print a
1.2 区间[0,1)均匀分布的桶排序
当输入符合均匀分布时,例如,元素均匀的分布在区间[0,1)上,可以将桶排序与其它排序方法结合使用。
如果序列的大小为n,就将[0,1)划分成n个相同大小的子区间(桶),然后将n个输入数分布到各个桶中。先对各个桶中的数进行排序,然后按照次序把各桶中的元素列出来即可。
《算法导论》的描述图:

代码:
class bucketSort(object):
def insertSort(self,a):
n=len(a)
if n<=1:
pass
for i in range(1,n):
key=a[i]
j=i-1
while key<a[j] and j>=0:
a[j+1]=a[j]
j-=1
a[j+1]=key
def sort(self,a):
n=len(a)
s=[[] for i in xrange(n)]
for i in a:
s[int(i*n)].append(i)
for i in s:
self.insertSort(i)
return [i for j in s for i in j]
def __call__(self,a):
return self.sort(a)
if __name__=='__main__':
from random import random
from timeit import Timer
a=[random() for i in xrange(10000)]
def test_bucket_sort():
bucketSort()(a)
def test_builtin_sort():
sorted(a)
tests=[test_bucket_sort,test_builtin_sort]
for test in tests:
name=test.__name__
t=Timer(name+'()','from __main__ import '+name)
print t.timeit(1)
2. 基数排序
基数排序一般用于长度相同的元素组成的数组。首先按照最低有效数字进行排序,然后由低位向高位进行。
329 720 720 329
457 355 329 355
657 436 436 436
839====≯ 457====≯ 839====≯ 457
436 657 355 657
720 329 457 720
355 839 657 839
基数排序可以看做是进行多趟桶排序。每个有效数字都在0-9之间,很适合桶排序,建10个桶很方便。
排序数组 64,8,216,512,27,729,0,1,343,125
第一趟排序:
0 1 512 343 64 125 216 27 8 729
0 1 2 3 4 5 6 7 8 9
第二趟排序:
8 729
1 216 27
0 512 125 343 64
0 1 2 3 4 5 6 7 8 9
第三趟排序:
64
27
8
1
0 125 216 343 512 729
0 1 2 3 4 5 6 7 8 9
输出:1 8 27 64 125 216 343 512 729
代码:
import random
def radixSort():
A=[random.randint(1,9999) for i in xrange(10000)]
for k in xrange(4): #4轮排序
s=[[] for i in xrange(10)]
for i in A:
s[i/(10**k)%10].append(i)
A=[a for b in s for a in b]
return A
1.3 计数排序
假设n个输入元素中每一个都是介于0到k之间的整数,此处k为某个整数。当k=O(n)时,计数排序的运行时间为Θ(n)。
对每一个数的元素x,确定出小于x的元素个数。有了这一信息就可以把x直接放到最终输出数组中的位置上。
def countingSort(alist,k):
n=len(alist)
b=[0 for i in xrange(n)]
c=[0 for i in xrange(k+1)]
for i in alist:
c[i]+=1
for i in xrange(1,len(c)):
c[i]=c[i-1]+c[i]
for i in alist:
b[c[i]-1]=i
c[i]-=1
return b
if __name__=='__main__':
a=[random.randint(0,100) for i in xrange(100)]
print countingSort(a,100)