本周任务:
请确保熟悉并理解机器学习数学部分常用相关概念:
1.高等数学
1)函数 2)极限 3)导数 4)极值和最值 5)泰勒级数 6)梯度 7)梯度下降
2.线性代数
1)基本概念 2)行列式 3)矩阵 4)最小二乘法 5)向量的线性相关性
3.概率论
1)事件 2)排列组合 3)概率 4)贝叶斯定理 5)概率分布 6)期望和方差 7)参数估计
2.本周视频学习内容:https://www.bilibili.com/video/BV1Tb411H7uC?p=2
1)P2 概率论与贝叶斯先验
2)P3 矩阵和线性代数
机器学习是一门多领域交叉学科,涉及较多的数学知识,本节课知识之前都有学过,这次根据重点重新梳理一遍,一定要多加重视。通过观看视频,大家对课程的数学基础部分加深印象。
建议大家边看边做笔记,记录要点及所在时间点,以便有必要的时候回看。学习笔记也是作业的一部分。
3.作业要求:
1)贴上视频学习笔记,要求真实,不要抄袭,可以手写拍照。
2)用自己的话总结“梯度”,“梯度下降”和“贝叶斯定理”,可以word编辑,可做思维导图,可以手写拍照,要求言简意赅、排版整洁。
1 贴上视频学习笔记,要求真实,不要抄袭,可以手写拍照。
1)P2 概率论与贝叶斯先验
(学习视频来自:https://www.bilibili.com/video/BV1Tb411H7uC?p=2)

视频进度- -23:50




视频进度- -43:37




学习进度- -61:00




学习进度- -103:28

学习进度- -137:46



学习进度- -147:00
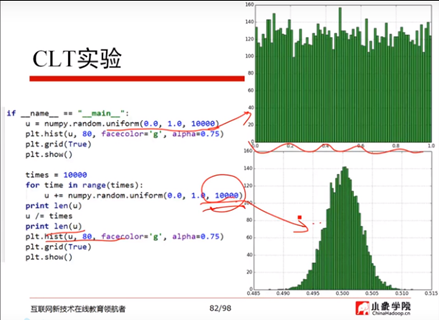
2)P3 矩阵和线性代数
(学习视频来自:https://www.bilibili.com/video/BV1Tb411H7uC?p=3)

学习进度- -16:04



学习进度- -32:00



学习进度- -57:15


学习进度- -94:05



2 用自己的话总结“梯度”,“梯度下降”和“贝叶斯定理”,可以word编辑,可做思维导图,可以手写拍照,要求言简意赅、排版整洁。
1)梯度
梯度本意是一个向量(矢量),当某一函数在某点处沿着该方向的方向导数取得该点处的最大值,即函数在该点处沿方向变化最快,变化率最大(为该梯度的模)。

用法:用于斜度
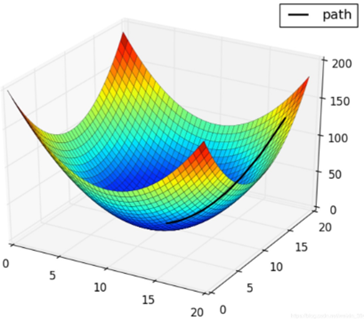
2)梯度下降
梯度下降法是一个最优化算法,通常也称为最速下降法。
最速下降法是求解无约束优化问题最简单和最古老的方法之一,虽然现在已经不具有实用性,但是许多有效算法都是以它为基础进行改进和修正而得到的。最速下降法是用负梯度方向为搜索方向的,最速下降法越接近目标值,步长越小,前进越慢。
用法:用于求解非线性方程组,常用于机器学习和人工智能当中用来递归性地逼近最小偏差模型。
缺点:
靠近极小值时收敛速度减慢。
直线搜索时可能会产生一些问题。
可能会“之字形”地下降。
3)贝叶斯定理
贝叶斯定理是关于随机事件A和B的条件概率(或边缘概率)的一则定理。其中P(A|B)是在B发生的情况下A发生的可能性。
公式:
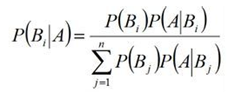
意义:
贝叶斯推理的问题是条件概率推理问题,这一领域的探讨对揭示人们对概率信息的认知加工过程与规律、指导人们进行有效的学习和判断决策都具有十分重要的理论意义和实践意义。