动态规划,借助矩阵可以直观的看到计算过程。
定义二维数组dp, dp[ i ][ j ],表示前 j 项所构成 i 子段的最大和,且必须包含着第j项,即以第j项结尾
然后是一个递推过程。
求dp[ i ][ j ],有两种情况
1、dp[ i ][ j ] = dp[ i ] [ j-1 ] + a[ j ] ,即把第j项融合到第 j-1 项的子段中,子段数没变
2、dp[ i ][ j ] = dp[ i-1 ] [ t ] + a[ j ],(i-1<= t < j )
把第 j 项作为单独的一个子段,然后找一下i-1个子段时,最大的和,然后加上a[ j ]
然后比较上面两种情况,取大的。
下面看图,红色数字为输入的序列:
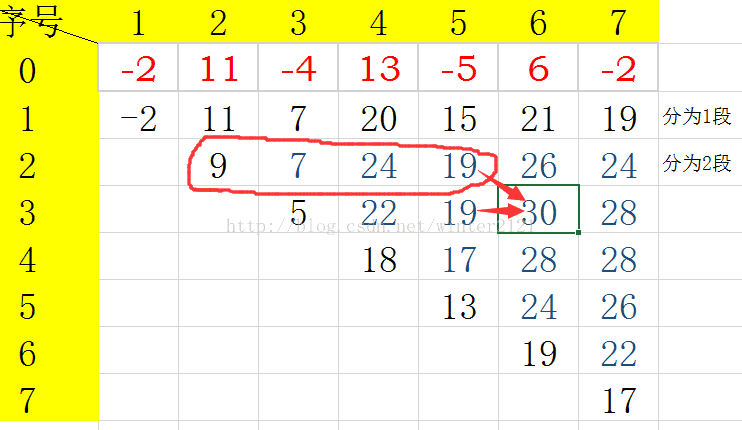
如图,要求dp[ 3 ][ 6 ],只需比较他左边的那个,和上面那一行圈起来的之中最大的数,
再加上a[ j ] 即为dp[ 3 ][ 6 ] 的值。
优化一下:
1、沿着第m行的最后一个元素,往左上方向画一条线,线右上方的元素是没必要计算的
那么dp[ i ][ j ] ,j++的时候,j的上限为 i + n - m 即可。
还有左下角那一半矩阵,也是不用计算的,因为1个数字不可能分为2个子段
2、每确定一个dp[ i ][ j ],只需用到本行和上一行,所以不用开维数组也可以,省内存。
开两个一维数组,pre和dp,pre记录上一行,dp记录当前行
3、再对上一行红圈中的数字找最大值时,若用一个循环来找,容易超时。
优化方法:在每次计算dp之前,同时记录下j前面的最大元素。
时间复杂度大致为O(m*(n-m+1)),mn-m方
通过图片,分析情况1和2,就能发现,从左上角走到第 m 行的最后一个元素即可,找出第 m 行的最大值即为答案。
三、例题
1、51nod 1052
1052 最大M子段和
基准时间限制:2 秒 空间限制:131072 KB 分值: 80 难度:5级算法题
N个整数组成的序列a[1],a[2],a[3],…,a[n],将这N个数划分为互不相交的M个子段,并且这M个子段的和是最大的。如果M
>= N个数中正数的个数,那么输出所有正数的和。
例如:-2 11 -4 13 -5 6 -2,分为2段,11
-4 13一段,6一段,和为26。
Input
第1行:2个数N和M,中间用空格分隔。N为整数的个数,M为划分为多少段。(2 <= N , M <= 5000)
第2 - N+1行:N个整数 (-10^9 <= a[i] <= 10^9)
第1行:2个数N和M,中间用空格分隔。N为整数的个数,M为划分为多少段。(2 <= N , M <= 5000)
第2 - N+1行:N个整数 (-10^9 <= a[i] <= 10^9)
Output
输出这个最大和
输出这个最大和
Input示例
7 2
-2
11
-4
13
-5
6
-2
7 2
-2
11
-4
13
-5
6
-2
Output示例
26
26
#include<cstdio> #include<iostream> #include<algorithm> #include<map> #include <math.h> #include<bits/stdc++.h> using namespace std; typedef long long ll; inline int read() { int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } const int INF=0x3f3f3f3f; const int maxn=1e6+100; int n,m; int a[maxn]; int dp[maxn]; int cmax[maxn]; int main(){ int n,m,Max; cin>>n>>m; for(int i=1;i<=n;i++){ cin>>a[i]; } for(int i=1;i<=m;i++){ Max=-INF; for(int j=i;j<=n;j++){ dp[j]=max(dp[j-1]+a[j],cmax[j-1]+a[j]); cmax[j-1]=Max; Max=max(Max,dp[j]); } } printf("%d",Max); }
例题2:
http://acm.hdu.edu.cn/showproblem.php?pid=1024
问题描述
现在我想你们已经了解伊格那丢了。L的“最大和”问题。为了做一个勇敢的演员,我们总是挑战自己去解决更困难的问题。现在你面临一个更困难的问题。
给定一个连续的数字序列S1, S2, S3, S4…Sx,……Sn(1≤x≤n≤1,000,000,-32768≤Sx≤32767)。我们定义了一个函数sum(i, j) = Si +…+ Sj(1≤i≤j≤n)
现在给定一个整数m(m > 0),你的任务是找到m对i和j,它们组成和(i1, j1) +和(i2, j2) +和(i3, j3) +…+和(im, jm)最大(ix≤iy≤jx或ix≤jy≤jx不允许)。
但是我很懒,我不想写一个特殊的判断模块,所以你不必输出m对I和j,只输出和(ix, jx)(1≤x≤m)的最大和。^ _ ^
输入
每个测试用例将以两个整数m和n开始,然后是n个整数S1, S2, S3…Sn。
处理到文件末尾。
输出
在一行中输出上面描述的最大总和。
样例输入
1 3 1 2 3
2 6 -1 4 -2 3 -2 3
样例输出
6
8
提示
建议使用大输入、scanf和动态编程。
#include<cstdio> #include<iostream> #include<algorithm> #include<map> #include <math.h> #include<bits/stdc++.h> using namespace std; typedef long long ll; inline int read() { int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } const int INF=0x3f3f3f3f; const int maxn=1e6+100; int n,m; int a[maxn]; int dp[maxn]; int cmax[maxn]; int main(){ int n,m; int Max; while(~scanf("%d%d",&m,&n)){ memset(dp,0,sizeof(dp)); memset(cmax,0,sizeof(cmax)); for(int i=1;i<=n;i++){ cin>>a[i]; } for(int i=1;i<=m;i++){ Max=-INF; for(int j=i;j<=n;j++){ dp[j]=max(dp[j-1]+a[j],cmax[j-1]+a[j]);//cmax是上一步的 cmax[j-1]=Max;//为i++后准备,而不是j++,, Max=max(Max,dp[j]); } } printf("%d ",Max); } }
#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> using namespace std; const int maxn = 1e6+10; const int INF = 0x7fffffff; int a[maxn]; int dp[maxn]; int Max[maxn];//max(dp[i-1][k])就是上一组0~j-1的最大值 int main(){ int n,m,mmax; while(~scanf("%d%d",&m,&n)){ for(int i = 1; i <= n; i++){ scanf("%d",&a[i]); } memset(dp,0,sizeof(dp)); memset(Max,0,sizeof(Max));//分成0组的全是0 for(int i = 1; i <= m; i++){//分成i组 mmax = -INF; for(int j = i; j <= n; j++){//前j个数分成i组,至少需要i个数 dp[j] = max(dp[j-1]+a[j],Max[j-1]+a[j]); //Max[j-1]目前代表的是分成i-1组前j-1个数的最大值,a[j]单独一组组成i组 //dp[j-1]代表j-1个数分成组,第j个数a[j]放在前面i组的一组中,两种方式选取较大者 Max[j-1] = mmax;//当前考虑的是j但是mmax是上一次循环得到的,所以更新的是j-1 mmax = max(mmax,dp[j]);//更新mmax,这样下次循环同样更新的是j-1 } //这样也就更新得到了分i组的Max,下次分i+1组的时候就可以使用了 } printf("%d ",mmax); } return 0; }
参考:
https://blog.csdn.net/winter2121/article/details/72848482
https://blog.csdn.net/onion___/article/details/79157809?depth_1.utm_source=distribute.pc_relevant.none-task&utm_source=distribute.pc_relevant.none-task